Iterative equation solving

[Sinistrum]

Hello dear community,

I would appreciate your help on following question, concerning the generation of a variable, which solves an equation, containing variables already existing in the data set, where the equation is not solved for the unknown but shall be solved iteratively.

In the following, I provide a simply example.

data icctrial;input p e1 e2 e3 r;
datalines;
48.159278738	10	20	30	0.1
80.681818182	20	40	60	0.2
456.46644799	30	45	601	0.15
420.4413418	454	5	5	0.11
4986.8628377	5445	12	45	0.17
0.7513148009	0	0	1	0.1
11.605639731	5	6	5	0.2
2.5476889974	1	2	1	0.3
;
run;

The equation to be solved for each observation is

p=(e1)/(1+a)+e2/((1+a)**2)+e3/((1+a)**3),

with "p", "e1", "e2" and "e3" all given, "a" as the only unknown.

The solution shall be added to the data set as the variable "a" for each observation.

The data is chosen, such that "r" is the correct solution. "r" is added as a reference (sadly, only).

I would be glad, if someone would help me.

Yours sincerely,

Sinistrum

[Reeza]

Have you looked at PROC MODEL? Do you have SAS ETS licensed?

http://support.sas.com/documentation/cdl/en/etsug/60372/HTML/default/viewer.htm#etsug_model_sect003....

[Sinistrum]

Hello

and thank you for your reply.

Indeed, during my desperate search, I came across "PROC MODEL".

As I have never worked with SAS before, I was afraid, this was "just" a tool in order to create the standard Least-Squares-Regression output . Furthermore, I do not know, how I could assign the output of such a procedure as a variable to my existing data set.

So, maybe I should dig deeper into that topic.

I was hoping for something profane in the manner like

data icctrial;
	set icctrial;
	a = 'such that this equation here is fulfilled';
run;

and that someone would have an easy solution,

But thanks to you, I now know where to search.

I hope I will come to terms with this issue.

---

Indeed, "I" have SAS/ETS licensed.

---

EDIT:

I tried this

proc model data=icctrial out=egal;
exogenous p e1 e2 e3;
endogenous a ;
solve a;
p=(e1)/(1+a)+e2/((1+a)**2)+e3/((1+a)**3);
run;

but it gives pretty inaccurate results.

[PGStats · Accepted solution]

You can also use the solve function in FCMP:

data test;
input p e1 e2 e3;
datalines;
48.159278738	10	20	30	
80.681818182	20	40	60	
456.46644799	30	45	601	
420.4413418	    454	5	5
4986.8628377	5445	12	45
0.7513148009	0	0	1
11.605639731	5	6	5
2.5476889974	1	2	1
;


/* FCMP routine to find function roots */
proc fcmp outlib=sasuser.fcmp.test;
function fn(e1, e2, e3, a);
    return ( e1/(1+a) + e2/(1+a)**2 + e3/(1+a)**3 );
endsub;
function findZero(p, e1, e2, e3, init);
    array solvopts[1] initial (0);
    initial = init;
    return (solve("fn", solvopts, p, e1, e2, e3, .)); 
endsub;
run;

options cmplib=sasuser.fcmp;
         
data roots;
set test;
root = findZero(p, e1, e2, e3, 0.1);
run;

proc print data=roots; run;

which gives the same roots as proc nlin.

[PGStats]

You don't need an iterative procedure to find the roots of third degree polynomials. But for a general function of one variable, you can hijack the line search of proc nlin in this way:

data test;
input p e1 e2 e3;
datalines;
48.159278738	10	20	30	
80.681818182	20	40	60	
456.46644799	30	45	601	
420.4413418	    454	5	5
4986.8628377	5445	12	45
0.7513148009	0	0	1
11.605639731	5	6	5
2.5476889974	1	2	1
;

/* Add equation number */
data parms;
set test;
eqNo + 1;
run;

/* define starting value for parameter b = 1+a */
data startingValues;
set parms;
parameter = "b";
Estimate = 1.1;
run;

/* Find 3rd degree equation root for every obs */
proc nlin data=parms outest=roots(where=(_TYPE_="FINAL"));
by eqNo p e1 e2 e3;
parameters / pdata=startingValues;
model e3 = -(-p*b**3 + e1*b**2 + e2*b);
run;

title "Polynomial roots";
proc sql;
select eqNo, p, e1, e2, e3, b-1 as a format=6.4,
    e3 + (-p)*b**3 + e1*b**2 + e2*b as rootValue
from roots
order by eqNo;
quit;

Note: Some roots don't match your 'r' values.

[Ksharp]

You are looking for the root of function : F(x)=p*x**3-e1*x**2-e2*x-e3  
It would be easy for SAS/IML . You can run it under SAS University Edition.



data icctrial;
infile cards expandtabs truncover;
input p e1 e2 e3 r;
datalines;
48.159278738	10	20	30	0.1
80.681818182	20	40	60	0.2
456.46644799	30	45	601	0.15
420.4413418	454	5	5	0.11
4986.8628377	5445	12	45	0.17
0.7513148009	0	0	1	0.1
11.605639731	5	6	5	0.2
2.5476889974	1	2	1	0.3
;
run;

proc iml;
use icctrial;
read all var _num_ into x[c=vnames];
close;

root=j(nrow(x),1,.);
do i=1 to nrow(x);
 parm=x[i,1]||-x[i,2]||-x[i,3]||-x[i,4]; 
 roots=polyroot(parm);
 root[i]=roots[loc(roots[,2]=0),1]-1;
end;
want=x||root;
print want[c=(vnames||'root') l=''];
quit;






OUTPUT:

p	e1	e2	e3	r	root
48.159279	10	20	30	0.1	0.1
80.681818	20	40	60	0.2	0.1898444
456.46645	30	45	601	0.15	0.1489363
420.44134	454	5	5	0.11	0.1004448
4986.8628	5445	12	45	0.17	0.1014909
0.7513148	0	0	1	0.1	0.1
11.60564	5	6	5	0.2	0.1791374
2.547689	1	2	1	0.3	0.2614769

[Sinistrum]

Thank you for your answers. This is really awesome.

So, "solve function in FCMP" and "hijack[ing] the line search of proc nlin" as you mentioned, PG, are presumably exactly what I am looking for.

The data set I made up was just a simple example. In fact, I do have to solve a function of the form 

,

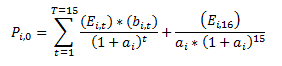
where the variable "b" is a function of "a" (and a constant, which is given, no problem with that), too.

So the itterative procedure is indeed what I am looking for.

Thank you, Ksharp, too. I am convinced I can make use of this later, too, for other approaches for different equations as the equation mentioned is not the only to be dealt with.

So, today I am going to play a little with your solution suggestions.

I just got the message by mail that my problem had been quasi-solved and just wanted to express real quickly my gratitude for and appreciation of your answers. Again, thank you very much.

What still makes me worry, though, is this one observation "5", where the true solution is 17% and not 10,15%. But I guess it is just due to the fact I mindlessly made up the data, the real sample I am dealing with does not contain such extreme values.

Best regards,

Sinistrum

[PGStats]

---

@Sinistrum wrote:

What still makes me worry, though, is this one observation "5", where the true solution is 17% and not 10,15%. But I guess it is just due to the fact I mindlessly made up the data, the real sample I am dealing with does not contain such extreme values.

---

Simple check for obs 5:

p - f(e1, e2, e3; 0.17) = 296.15,  

p - f(e1, e2, e3; 0.1015) = 0.0002
 

[Sinistrum]

So, obviously, I am even to clusmy to set up test-data-sets properly for I have made a mistake with discounting e1.

The correct data is

data test;
input p e1 e2 e3 r;
datalines;
48.159278738	10	20	30	0.1
79.166666667	20	40	60	0.2
455.28067724	30	45	601	0.15
416.72307808	454	5	5	0.11
4690.7089915	5445	12	45	0.17
0.7513148009	0	0	1	0.1
11.226851852	5	6	5	0.2
2.4078288575	1	2	1	0.3;
run;

With this now corrected data, the estimated "root" matches the "r".

So sorry for this and, once again, thank you very much.

Best regards,

Sinistrum