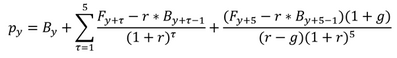Solving Equation

[MAC1430]

Hi everyone,

I want to solve equation below to calculate r for each stock:

data test;
input stock$     y	B	P	F	g;
datalines;
A	1	12.1492	80.16	3.8886	0.3038
A	2	15.3785	63.54	4.8659	0.3769
A	3	11.5507	41.19	4.5454	0.205
A	4	15.1777	35.28	4.3858	0.1478
A	5	14.9545	52	5.7079	0.0644
A	6	15.8837	50.78	6.1861	-0.0636
A	7	19.3065	67.64	6.7226	-0.0915
A	8	21.6415	72.05	7.7686	-0.0553
A	9	23.6561	74.51	8.804	0.0005
A	10	27.2373	43.05	9.0739	0.123
B	1	6.3668	37.8	2.7893	0.3038
B	2	7.6967	35.4	3.238	0.3769
B	3	8.6812	29.3	3.2122	0.205
B	4	8.999	30.9	3.2352	0.1478
B	5	9.5064	29.75	3.5381	0.0644
B	6	10.1293	39.3	3.4308	-0.0636
B	7	12.2344	43.3	3.7561	-0.0915
B	8	13.2885	52	4.2523	-0.0553
B	9	13.9864	41.6	4.7464	0.0005
B	10	14.043	50.2	4.2598	0.123
C	1	1.4639	24.19	0.3939	0.3038
C	2	2.3384	19.52	1.3403	0.3769
C	3	2.626	7.96	-1.0251	0.205
C	4	2.7283	15.72	0.3156	0.1478
C	5	2.3651	11.81	0.049	0.0644
C	6	2.8771	16.9	0.964	-0.0636
C	7	3.532	18.84	1.1485	-0.0915
C	8	4.5199	21.66	2.0169	-0.0553
C	9	4.379	12.75	2.0582	0.0005
C	10	4.6028	24	0.9412	0.123
;

If you know a solution to this problem, please comment, it is very much appreciated.

[sbxkoenk]

Hello,

That's "just" algebra and that can de done with PROC IML.

But for PROC IML, you need a license for SAS/IML (Interactive Matrix Language).

You can also do it with SAS/ETS (Econometrics and Time Series).

PROC MODEL or PROC TMODEL (multithreaded version of PROC MODEL) can be used for solving equations.

Maybe PROC SYSLIN is suited as well?

If you do not have SAS/IML nor SAS/ETS, it can probably be done with the data step as well (possibly in combination with PROC FCMP), but then you need to do some more preparation work to disentangle the formula.

Good luck,

Koen

[FreelanceReinh]

Hi @MAC1430,

---

@MAC1430 wrote:

I want to solve equation below to calculate r for each stock:

---

At first glance this formula looks similar to that in your previous post. However, the second of the two fractions now contains t, which implies that it belongs under the sum (t=1, ..., 5). But then the two fractions should be put into parentheses and also the first fraction could be factored out, which would simplify the formula. In your previous post the second fraction used the constant 5 instead of t, suggesting that it does not belong under the sum (t=1, ..., 5) -- which I've realized now. I have edited yesterday's solution accordingly. Sorry for the confusion.

Please double-check if your new formula is correct as posted or if the second fraction should contain something else in place of t (similar to yesterday's formula).

Either way the PROC FCMP code for the new formula will be analogous to yesterday's solution.

[MAC1430]

Hi Reinhard,

Thank you very much for the comment.

I updated the formula, you are right, the second fraction is not part of the sum function (I should have checked it more carefully, my bad).

What I'm confused about the new equation is, the unknown r, is embeded in both numerator   and denominator .

In the first equation, the unknown is only in the denominator.

Could you pls kindly show on how to solve the new equation using proc fcmp?

Sorry, I'm not farmilar with this function, thus asking you again, your help is Veryyy much appreciated.

[FreelanceReinh]

Thanks for the updated formula and also for providing realistic sample data (in usable form).

The right-hand side of the equation -- a rational function in r -- has singularities (poles) at r=−1 and r=g. I've examined a few particular cases and the common pattern was: one solution on each side of the pole at r=−1 and one solution in a neighborhood of the pole at r=g. So the first question is: Which of the three solutions do you want? For the time being I have focused on the solution near r=g because it was always positive. But this is not guaranteed in general since g can be negative, as we see in the sample data. It also depends on the data whether r₀<g or r₀>g for the solution r₀ near r=g. This is a challenge for the SOLVE function because it requires an initial value as a starting point and it's likely a good idea to stay on one side of the pole at r=g while searching for the solution. The sign of the numerator of the last fraction seemed to be a useful criterion to distinguish between the two cases r₀<g and r₀>g. It worked for your sample data, but you may need to modify the criterion for (very) different data. To avoid difficulties with the pole, I've introduced a new (FCMP-internal) variable x so that the solution can be written as r₀ = g ± exp(−x*10000) with "+" or "-" depending on the sign of the numerator of the last fraction. Thus the SOLVE function can solve for x and the default initial value 0.001 is suitable (at least for your sample data).

I don't know the technical term for the rate (?) r and therefore named the function XRATE.

Here is the code (allowing for y values up to 99 -- simply increase the array dimensions if you need more):

/* Define function XRATE */

proc fcmp outlib=work.funcs.test;
function rs(y, B[*], F[*], g, x);
  s=B[y];
  z=sign((F[y+5]-g*B[y+4])*(1+g))*exp(-x*1e4);
  do tau=1 to 5;
    s = s + (F[y+tau]-(g+z)*B[y+tau-1])/(1+g+z)**tau;
  end;
  s = s + (F[y+5]-(g+z)*B[y+4])*(1+g)/(z*(1+g+z)**5);
  return(s);
endfunc;
function xrate(y, p[*], B[*], F[*], g);
  r=g+sign((F[y+5]-g*B[y+4])*(1+g))*exp(-solve("RS", {.}, p[y], y, B, F, g, .)*1e4);
  return(r);
endfunc;
run;

/* Make function available */

options cmplib=work.funcs;

/* Apply function XRATE to dataset TEST */

data want;
array _B[99] _temporary_;
array _P[99] _temporary_;
array _F[99] _temporary_;
do until(last.stock);
  set test;
  by stock;
  _B[y]=B;
  _P[y]=P;
  _F[y]=F;
end;
do until(last.stock);
  set test;
  by stock;
  r=xrate(y,_P,_B,_F,g);
  output;
end;
call missing(of _B[*], of _P[*], of _F[*]);
run;

Not surprisingly, the solutions for y>5 are missing because the formula contains indices up to y+5, while 10 is the maximum of y in the sample data. Note that all solutions are greater than the respective g, except for the case stock='B' & y=2, where the solution is found on the left side of the pole at r=g because the sign(...) term is negative.

As explained above, the SOLVE function (using the Gauss-Newton method) is maybe not ideal for a function with poles like this. So, if difficulties arise with your real data, you may want to explore other possibilities such as the FROOT function mentioned by @Rick_SAS in the previous thread. I couldn't test that because SAS/IML is not contained in my SAS license.

[MAC1430]

Thank you very much for the code and explanation around it.

This is new knowledge and a learning process for me, if it's convenient, Could you kindly shed light on how the other solution on each side of the pole at r=−1 looks like, using the SOLVE function?

Appreciate it.

Mac

[FreelanceReinh · Accepted solution]

I have extended the function definitions to include a new first argument w, whose value 1, 2 or 3 determines whether a solution is searched < −1, > −1 or near g. The corresponding solutions, if any, are stored in variables r1, r2 and r3, respectively.

/* Define function XRATE */

proc fcmp outlib=work.funcs.test;
function rs(w, y, B[*], F[*], g, x);
  select(w);
    when(1) z=-1-exp(-x*1e4); /* for a solution < -1 */
    when(2) z=-1+exp(-x*1e4); /* for a solution > -1 */
    when(3) z=g+sign((F[y+5]-g*B[y+4])*(1+g))*exp(-x*1e4); /* for a solution near g */
  end;
  s=B[y];
  do tau=1 to 5;
    s = s + (F[y+tau]-z*B[y+tau-1])/(1+z)**tau;
  end;
  s = s + (F[y+5]-z*B[y+4])*(1+g)/((z-g)*(1+z)**5);
  return(s);
endfunc;
function xrate(w, y, p[*], B[*], F[*], g);
  array solvopts[5] initial abconv relconv maxiter status (0.001 0.001 1.0e-6 100);
  t=exp(-solve("RS", solvopts, p[y], w, y, B, F, g, .)*1e4);
  select(w);
    when(1) r=-1-t; /* solution < -1 */
    when(2) r=-1+t; /* solution > -1 */
    when(3) r=g+sign((F[y+5]-g*B[y+4])*(1+g))*t; /* solution near g */
  end;
  return(r);
endfunc;
run;

/* Make function available */

options cmplib=work.funcs;

/* Apply function XRATE to dataset TEST */

data want;
array _B[99] _temporary_;
array _P[99] _temporary_;
array _F[99] _temporary_;
do until(last.stock);
  set test;
  by stock;
  _B[y]=B;
  _P[y]=P;
  _F[y]=F;
end;
do until(last.stock);
  set test;
  by stock;
  r1=xrate(1,y,_P,_B,_F,g);
  r2=xrate(2,y,_P,_B,_F,g);
  r3=xrate(3,y,_P,_B,_F,g);
  output;
end;
call missing(of _B[*], of _P[*], of _F[*]);
run;

With your sample data, r3 contains the solution near g which we already found with the previous code version. In 12 of the 15 cases with potential solutions there are also (negative) solutions in r1 and r2. Unfortunately, the remaining three cases cause error messages "ERROR: Exception occurred during subroutine call" in the log. As it turned out (I checked this only with simplified input data), it is possible that both solutions near −1 are < −1, i.e., on the left side of the first pole. Hence, a missing value in r2 would be the expected result, but a failed search for the non-existent solution in the interval (−1, g] might run into the second pole, g.

Considering the graphs of some of the functions it seems possible theoretically that even more different cases exist -- depending on the data --, e.g., only one or no solution near −1 or more than three solutions. After all, the polynomial in r in the denominator has degree 5, so the graph is very "flexible" and thus challenging for a root-finding algorithm that uses derivatives. Maybe a different algorithm (than what is implemented in the SOLVE function) would be more suitable for your application, e.g., the bisection method. A sophisticated version of this is used by the FROOT function in SAS/IML. In its basic form it is also implemented in the %Bisect macro found in the SESUG 2007 paper Customized Base SAS implemented solvers. I used this macro occasionally in the past, but haven't applied it to your function yet.

Both the %Bisect macro and the SOLVE function would need carefully selected initial values to find all solutions in some cases. I've introduced an "options array" (cf. documentation) into the code to facilitate testing different initial values (first element of the array solvopts). The question remains whether all (positive and negative) solutions are really sensible to interpret in practice.

[MAC1430]

Thank you very much, it works fine 🙂