- Home
- /
- Programming
- /
- SAS Procedures
- /
- Re: How to calculate confidence interval for crude rate by using age g...
- RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
- Mark as New
- Bookmark
- Subscribe
- Mute
- RSS Feed
- Permalink
- Report Inappropriate Content
I am new to SAS and would like to solve I guess pretty simple task
I have the following data for incidences of the decease for each of 9 age groups for 17 years (2001-2017) and population in each age group
Here is data for 2001 year
Age Count Population
00-19 46 17945108
20-29 150 10460561
..............................................
85+ 109 1066463
And I need to calculate crude rate per 100000 with 95% CI intervals for all years using exact Poisson method.
Year Crude rate Low High
2001 .... ... ...
..............................................
2017 .... ... ...
I think it could be done by using one of the SAS proc but I do not know which one and how.
Could anyone help me to solve this?
Thank you very much in advance
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- RSS Feed
- Permalink
- Report Inappropriate Content
Hi @nastya,
Thanks for sharing the link to openepi.com. This is interesting. Now it's easy to provide SAS code:
/* Create sample data
(n=Number of cases, pt=person-time, ptu=person-time unit) */
data have;
input n pt ptu;
cards;
5 25 10
4060 76513290 100000
;
/* Compute crude rate with two confidence intervals:
exact Poisson CI and Byar's approximation */
%let alpha=0.05;
data want;
set have;
rate=n/pt*ptu;
lcl_exact=cinv(&alpha/2,2*n)/2/pt*ptu;
ucl_exact=cinv(1-&alpha/2,2*(n+1))/2/pt*ptu;
lcl_Byar=max(n*(1-1/(9*n)-probit(1-&alpha/2)/3*sqrt(1/n))**3/pt*ptu,0);
ucl_Byar=(n+1)*(1-1/(9*(n+1))+probit(1-&alpha/2)/3*sqrt(1/(n+1)))**3/pt*ptu;
run;
proc print data=want;
run;Result:
lcl_ ucl_ n pt ptu rate exact exact lcl_Byar ucl_Byar 5 25 10 2.00000 0.64939 4.66733 0.64454 4.66727 4060 76513290 100000 5.30627 5.14429 5.47205 5.14429 5.47205
I used your example and the example in the documentation https://www.openepi.com/PDFDocs/PersonTime1Doc.pdf, p. 2, in dataset HAVE.
For the exact CI the openepi online calculator uses an iterative algorithm based on the Poisson probability function, whereas my SAS code uses the well-known relationship between the Poisson and chi-square distributions. Note that the formula for the lower confidence limit in the openepi documentation (see link above), p. 3, section "Fisher's exact test," is incorrect: The upper summation limit should read a-1, not a. The corresponding Javascript code is correct (in this regard), though.
You'll notice that the value of lcl_Byar in the first observation of WANT (after rounding to four decimals) does not exactly match the 0.6446 from the documentation. But SAS is -- of course! -- correct here. Unlike SAS's PROBIT function, the openepi source code computes the 97.5% quantile of the standard normal distribution as the square root of a hard-coded (!), rounded 95% quantile of the chi-square distribution with one degree of freedom (3.841). Using this value the result would be 0.644588..., which explains the minor difference. Other than that, I used the formulas under "Byar Method" (p. 3) in the openepi documentation.
Please note that, for simplicity, I did not implement openepi's rule for the extreme cases n=0 or pt=0.
- Mark as New
- Bookmark
- Subscribe
- Mute
- RSS Feed
- Permalink
- Report Inappropriate Content
This may be the answer.
I used this google search to find it
poisson confidence limit site:sas.com
- Mark as New
- Bookmark
- Subscribe
- Mute
- RSS Feed
- Permalink
- Report Inappropriate Content
I think the OP should also use some numeric representation of each group. For example, the median age in each group, or the center of each group (10, 25, 35, ....). Do you concur, Doc?
- Mark as New
- Bookmark
- Subscribe
- Mute
- RSS Feed
- Permalink
- Report Inappropriate Content
Thank you for your response @Rick_SAS !
I kind of know what the numeric result should be. Our previous statistician calculated for one set of data. I need to repeat calculation for another set.
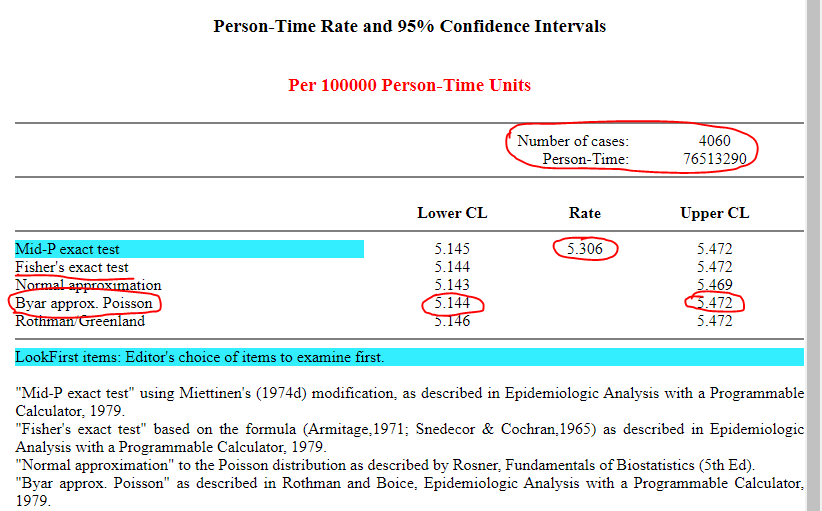
I found that online tool openepi ( https://www.openepi.com/PersonTime1/PersonTime1.htm) can produce rate and CI intervals exactly as in his original calculation.
Please see screenshot below
The number of cases I entered in that tool is total count of cases for all ages for 2001.
Person-time is total population for all ages for 2001.
Based on results above Poisson approx. and Fisher's exact test give me original result by just providing these two numbers above.
I prefer to use Poison approx. as I found in statistician notes he used exact Poisson method.
I would greatly appreciate your help in how to get this result in SAS just for one year. I can run then for all years
Thank you!
- Mark as New
- Bookmark
- Subscribe
- Mute
- RSS Feed
- Permalink
- Report Inappropriate Content
Hi @nastya,
Thanks for sharing the link to openepi.com. This is interesting. Now it's easy to provide SAS code:
/* Create sample data
(n=Number of cases, pt=person-time, ptu=person-time unit) */
data have;
input n pt ptu;
cards;
5 25 10
4060 76513290 100000
;
/* Compute crude rate with two confidence intervals:
exact Poisson CI and Byar's approximation */
%let alpha=0.05;
data want;
set have;
rate=n/pt*ptu;
lcl_exact=cinv(&alpha/2,2*n)/2/pt*ptu;
ucl_exact=cinv(1-&alpha/2,2*(n+1))/2/pt*ptu;
lcl_Byar=max(n*(1-1/(9*n)-probit(1-&alpha/2)/3*sqrt(1/n))**3/pt*ptu,0);
ucl_Byar=(n+1)*(1-1/(9*(n+1))+probit(1-&alpha/2)/3*sqrt(1/(n+1)))**3/pt*ptu;
run;
proc print data=want;
run;Result:
lcl_ ucl_ n pt ptu rate exact exact lcl_Byar ucl_Byar 5 25 10 2.00000 0.64939 4.66733 0.64454 4.66727 4060 76513290 100000 5.30627 5.14429 5.47205 5.14429 5.47205
I used your example and the example in the documentation https://www.openepi.com/PDFDocs/PersonTime1Doc.pdf, p. 2, in dataset HAVE.
For the exact CI the openepi online calculator uses an iterative algorithm based on the Poisson probability function, whereas my SAS code uses the well-known relationship between the Poisson and chi-square distributions. Note that the formula for the lower confidence limit in the openepi documentation (see link above), p. 3, section "Fisher's exact test," is incorrect: The upper summation limit should read a-1, not a. The corresponding Javascript code is correct (in this regard), though.
You'll notice that the value of lcl_Byar in the first observation of WANT (after rounding to four decimals) does not exactly match the 0.6446 from the documentation. But SAS is -- of course! -- correct here. Unlike SAS's PROBIT function, the openepi source code computes the 97.5% quantile of the standard normal distribution as the square root of a hard-coded (!), rounded 95% quantile of the chi-square distribution with one degree of freedom (3.841). Using this value the result would be 0.644588..., which explains the minor difference. Other than that, I used the formulas under "Byar Method" (p. 3) in the openepi documentation.
Please note that, for simplicity, I did not implement openepi's rule for the extreme cases n=0 or pt=0.
- Mark as New
- Bookmark
- Subscribe
- Mute
- RSS Feed
- Permalink
- Report Inappropriate Content
Hi @FreelanceReinh !
Thank you very much for your detailed explanation and source code.
That was exactly what I needed.
Cheers
April 27 – 30 | Gaylord Texan | Grapevine, Texas
Registration is open
Walk in ready to learn. Walk out ready to deliver. This is the data and AI conference you can't afford to miss.
Register now and lock in 2025 pricing—just $495!
Learn the difference between classical and Bayesian statistical approaches and see a few PROC examples to perform Bayesian analysis in this video.
Find more tutorials on the SAS Users YouTube channel.
SAS Training: Just a Click Away
Ready to level-up your skills? Choose your own adventure.