- RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
- Mark as New
- Bookmark
- Subscribe
- Mute
- RSS Feed
- Permalink
- Report Inappropriate Content
Suppose X = 1,2,3,4,5,6,7 and P(X=x)=0.009, 0.001, 0.036, 0.027, 0.145 0.309, 0.473 resulting in E(X)=6.117. We can simulate from this distribution using
%let p=0.009 0.001 0.036 0.027 0.145 0.309 0.473;
%let seed=123456;
%let samplesize=1000;
%let delta=0.7; *mean difference;
data sample(keep= id x group);
call streaminit(&seed);
array p[6] (0.009 0.001 0.036 0.027 0.145 0.309); *p of the last category (7) is left out ;
do ID = 1 to &samplesize;
x = rand("Table", of p
group=1;
output;
end;
run;
OR
proc iml;
x = 1:7;
ExpVal=sum(x#{&p});
call randseed(&seed);
group1 = sample(x, &samplesize, "Replace", {&p});
quit;
My questions are the following;
(1) How can I modify P(X=x) such that E(X) is e.g., 5.5 (from 6.117) for group 1, assuming equal variances? So a shift of E(X) downwards.
(2) If I have a second group (group=2), how can I adapt the above code to result in a mean difference (delta=0.3 or 0.7) with group 2 always being higher, considering boundary limitations towards the last category (X=7)? A shift of E(X) upwards.
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- RSS Feed
- Permalink
- Report Inappropriate Content
HoHo. You seems to do some linear program . You should post it at OR forum , and I think there should be lots of solution .
The following is the solution from IML.
proc iml;
p={0.009 0.001 0.036 0.027 0.145 0.309 0.473};
x=1:7;
mean=(p#x)[+];
var=(p#((x-mean)##2))[+];
print mean var;
v=(x-5.5)##2; /*calculated var coefficient*/
print v[f=best8.];
/*Start Solution*/
object = { 1 1 1 1 1 1 1 };
coef = {1 2 3 4 5 6 7, /*mean */
20.25 12.25 6.25 2.25 0.25 0.25 2.25 , /* var coefficient e.g row vector V */
1 1 1 1 1 1 1 /* sum of p is 1 */
};
b = { 5.5 ,1.277311,1 };
l = { 0.01 0.01 0.01 0.01 0.01 0.01 0.01};
u = { 0.9 0.9 0.9 0.9 0.9 0.9 0.9};
rowsense = {'E','E','E'};
cntl= -1;
call lpsolve (rc,objv,solution,dual,rd,object,coef,b,cntl,rowsense,,l,u);
print solution ;
quit;
Xia Keshan
- Mark as New
- Bookmark
- Subscribe
- Mute
- RSS Feed
- Permalink
- Report Inappropriate Content
When you say "assuming equal variances" do you mean that the new probabilities give rise to a variance that is the same as for this example?
Define
p = {&p}`;
The variance is sum(x## # p) - ExpVal##2 = 1.277.;
The p vector is a 7-element vector with 6 free parameters (since sum(p)=1).
It looks like the problem is linear in the parameters p, so I would attempt to solve this as a linear programming problem.
The constraints are p[1]>0, ..., p[7]>0, sum(p)=1, mean=5.5, and Variance=1.277.
If you are using a recent version of SAS/IML, you can use the LPSOLVE call to solve LP problems. For older versions of IML, use the LP call.
I think there might be infinitely many solutions to your problem.
- Mark as New
- Bookmark
- Subscribe
- Mute
- RSS Feed
- Permalink
- Report Inappropriate Content
HoHo. You seems to do some linear program . You should post it at OR forum , and I think there should be lots of solution .
The following is the solution from IML.
proc iml;
p={0.009 0.001 0.036 0.027 0.145 0.309 0.473};
x=1:7;
mean=(p#x)[+];
var=(p#((x-mean)##2))[+];
print mean var;
v=(x-5.5)##2; /*calculated var coefficient*/
print v[f=best8.];
/*Start Solution*/
object = { 1 1 1 1 1 1 1 };
coef = {1 2 3 4 5 6 7, /*mean */
20.25 12.25 6.25 2.25 0.25 0.25 2.25 , /* var coefficient e.g row vector V */
1 1 1 1 1 1 1 /* sum of p is 1 */
};
b = { 5.5 ,1.277311,1 };
l = { 0.01 0.01 0.01 0.01 0.01 0.01 0.01};
u = { 0.9 0.9 0.9 0.9 0.9 0.9 0.9};
rowsense = {'E','E','E'};
cntl= -1;
call lpsolve (rc,objv,solution,dual,rd,object,coef,b,cntl,rowsense,,l,u);
print solution ;
quit;
Xia Keshan
- Mark as New
- Bookmark
- Subscribe
- Mute
- RSS Feed
- Permalink
- Report Inappropriate Content
This seems to be a completely appropriate question for the IML forum.
- Mark as New
- Bookmark
- Subscribe
- Mute
- RSS Feed
- Permalink
- Report Inappropriate Content
Hope so . Rick . ![]()
- Mark as New
- Bookmark
- Subscribe
- Mute
- RSS Feed
- Permalink
- Report Inappropriate Content
Thanks Rick and Xia.
Rick, Indeed I meant that the new probabilities would give rise to the same variance.
Xia, the solution you provide is what I needed for part 1 of my question (which is to obtain E(X)=5.5). I modified your code to include the sampling for the two groups. Many thanks.
However, for part 2 of my question, if for example, E(X) should become 6.867 (which would be a shift upwards of 0.75), the lpsolve call returns 0's for the solution. I think this is because the desired E(X)=6.867 is too close to the maximum score (7) inducing boundary problems. Are there any alternatives to dealing with this?
%let seed=123456;
%let samplesize=1000000;
%let delta=0.75; * mean difference or shift ;
proc iml;
p={0.009 0.001 0.036 0.027 0.145 0.309 0.473};
x=1:7;
mean=(p#x)[+];
var=(p#((x-mean)##2))[+];
print mean var;
expectmean=mean + δ * mean shifted by delta ;
v=(x-expectmean)##2; /*calculated var coefficient*/
print expectmean, v[f=best8.];
/*Start Solution*/
object = { 1 1 1 1 1 1 1 };
coef=x//v//object;
print coef;
b = expectmean // var // {1};
l = { 0.00001 0.00001 0.00001 0.00001 0.00001 0.00001 0.00001};
u = { 0.9999 0.9999 0.9999 0.9999 0.9999 0.9999 0.9999};
rowsense = {'E','E','E'};
cntl= -1;
call lpsolve (rc,objv,solution,dual,rd,object,coef,b,cntl,rowsense,,l,u);
print solution ;
mean2=(solution`#x)[+];
var2=(solution`#((x-mean2)##2))[+];
print mean var mean2 var2;
/* Sampling for the two groups */
call randseed(&seed);
group1 = sample(x, &samplesize, "Replace", p);
group2 = sample(x, &samplesize, "Replace", solution);
print (mean(group1`))[label="Sample mean group 1"] (var(group1`))[label="Sample Variance Group 1"],
(mean(group2`))[label="Sample mean group 2"] (var(group2`))[label="Sample variance group 2"];
quit;
- Mark as New
- Bookmark
- Subscribe
- Mute
- RSS Feed
- Permalink
- Report Inappropriate Content
For you second question, I don't understand "considering boundary limitations towards the last category (X=7)" , you want only change P(x=7) and keep other the same ? But if others have been settled ,then P(x=7) is all settled .
If you only want change E(X) = E(X)+0.3 =6.417, that would be easy .
proc iml;
p={0.009 0.001 0.036 0.027 0.145 0.309 0.473};
x=1:7;
mean=(p#x)[+] ;
var=(p#((x-mean)##2))[+];
print mean var;
v=(x-6.417 /*Delta is 0.3*/)##2; /*calculated var coefficient*/
print v[f=best8.];
/*Start Solution*/
object = { 1 1 1 1 1 1 1 };
coef = {1 2 3 4 5 6 7}//v//{1 1 1 1 1 1 1};
b = { 6.417 /*Delta is 0.3*/}//var//{1};
l = { 0.01 0.01 0.01 0.01 0.01 0.01 0.01};
u = { 0.9 0.9 0.9 0.9 0.9 0.9 0.9};
rowsense = {'E','E','E'};
cntl= -1;
call lpsolve (rc,objv,solution,dual,rd,object,coef,b,cntl,rowsense,,l,u);
print solution ;
mean=(solution`#x)[+] ;
var=(solution`#((x-mean)##2))[+];
print mean var;
quit;
Xia Keshan
- Mark as New
- Bookmark
- Subscribe
- Mute
- RSS Feed
- Permalink
- Report Inappropriate Content
Hi Xia Keshan!
Indeed, everything works well when newExpectedValue=E(X) + delta as long as delta is less than or equal to 0.66 (leading to newExpectedValue=6.77). The second question is simply a need to shift E(X) from 6.11 to 6.86 (delta=0.75).
- Mark as New
- Bookmark
- Subscribe
- Mute
- RSS Feed
- Permalink
- Report Inappropriate Content
if E(X) should become 6.867, I am kind of get feeling LPSOLVE() can't do that , unless sum of p could greater than 1.
or you could post it at OR forum , and see if somebody have a better method .
- Mark as New
- Bookmark
- Subscribe
- Mute
- RSS Feed
- Permalink
- Report Inappropriate Content
Lots of thanks though!
- Mark as New
- Bookmark
- Subscribe
- Mute
- RSS Feed
- Permalink
- Report Inappropriate Content
Hi. If you allow a little offset , you could try this:
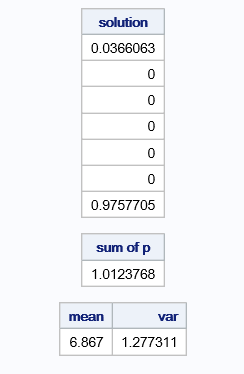
proc iml;
p={0.009 0.001 0.036 0.027 0.145 0.309 0.473};
x=1:7;
mean=(p#x)[+] ;
var=(p#((x-mean)##2))[+];
print mean var;
v=(x-6.867)##2; /*calculated var coefficient*/
print v[f=best8.];
/*Start Solution*/
object = { 0 0 0 0 0 0 0 };
coef = {1 2 3 4 5 6 7}//v//{1 1 1 1 1 1 1};
b = { 6.867}//var//{1};
l = {0 0 0 0 0 0 0 };
u = {1 1 1 1 1 1 1 };
rowsense = {'E','E','G'} ;
cntl= -1;
call lpsolve (rc,objv,solution,dual,rd,object,coef,b,cntl,rowsense,,l,u);
print solution ,(solution[+])[label='sum of p'];
mean=(solution`#x)[+] ;
var=(solution`#((x-mean)##2))[+];
print mean var;
quit;
Xia Keshan
- Mark as New
- Bookmark
- Subscribe
- Mute
- RSS Feed
- Permalink
- Report Inappropriate Content
Hi Xia,
I would prefer not to have an offset. But am so thankful for your efforts.
- Ask the Expert: The AI Advantage: How SAS Customer Intelligence 360 Solves Real Marketing Challenges | 27-Jan-2026
- DCSUG presents SAS OnDemand for Academics: the Easy Way to Learn SAS For Free for Students, Educator | 27-Jan-2026
- Ask the Expert: How to Supercharge Enterprise Agentic Workflows With SAS Retrieval Agent Manager | 05-Feb-2026
- Ask the Expert - Génération de données synthétiques : innovation et confidentialité | 10-Feb-2026
- Ask the Expert: Implementing a Digital Twin for the Monopoly Board Game Using SAS® Viya® | 12-Feb-2026
- SAS CI360 Tips and Tricks: Quick Wins, Shortcuts and Hidden Features Every Marketer Should Know | 17-Feb-2026
- SAS Bowl LIX, Integrating SAS and Git | 18-Feb-2026



