Modify a discrete distribution to yield given expected value

[KGeorge]

Suppose X = 1,2,3,4,5,6,7 and P(X=x)=0.009, 0.001, 0.036, 0.027, 0.145 0.309, 0.473 resulting in E(X)=6.117. We can simulate from this distribution using

%let p=0.009 0.001 0.036 0.027 0.145 0.309 0.473;

%let seed=123456;

%let samplesize=1000;

%let delta=0.7; *mean difference;

data sample(keep= id x group);

call streaminit(&seed);

array p[6] (0.009 0.001 0.036 0.027 0.145 0.309); *p of the last category (7) is left out ;

do ID = 1 to &samplesize;

   x = rand("Table", of p

);

   group=1;

   output;

end;

run;

OR

proc iml;

x = 1:7;

ExpVal=sum(x#{&p});

call randseed(&seed);

group1 = sample(x, &samplesize, "Replace", {&p});

quit;

My questions are the following;

(1) How can I modify P(X=x) such that E(X) is e.g., 5.5 (from 6.117) for group 1, assuming equal variances? So a shift of E(X) downwards.

(2) If I have a second group (group=2), how can I adapt the above code to result in a mean difference (delta=0.3 or 0.7) with group 2 always being higher, considering boundary limitations towards the last category (X=7)? A shift of E(X) upwards.

[Rick_SAS]

When you say "assuming equal variances" do you mean that the new probabilities give rise to a variance that is the same as for this example?

Define

p = {&p}`;

The variance is sum(x## # p) - ExpVal##2 = 1.277.;

The p vector is a 7-element vector with 6 free parameters (since sum(p)=1).

It looks like the problem is linear in the parameters p, so I would attempt to solve this as a linear programming problem.

The constraints are p[1]>0, ..., p[7]>0, sum(p)=1, mean=5.5, and Variance=1.277.

If you are using a recent version of SAS/IML, you can use the LPSOLVE call to solve LP problems. For older versions of IML, use the LP call.

I think there might be infinitely many solutions to your problem.

[Ksharp · Accepted solution]

HoHo. You seems to do some linear program . You should post it at OR forum , and I think there should be lots of solution .

The following is the solution from IML.

proc iml;
p={0.009 0.001  0.036  0.027  0.145  0.309  0.473};
x=1:7;
mean=(p#x)[+];
var=(p#((x-mean)##2))[+];
print mean var;

v=(x-5.5)##2; /*calculated var coefficient*/
print v[f=best8.];




/*Start Solution*/
object = { 1 1 1 1 1 1 1 };
coef = {1 2 3 4 5 6 7, /*mean */
  20.25  12.25  6.25  2.25   0.25   0.25 2.25 , /* var coefficient e.g row vector V */
  1 1 1 1 1 1 1 /* sum of p is 1 */
};
b = { 5.5 ,1.277311,1 };
l = { 0.01 0.01 0.01 0.01 0.01 0.01 0.01};
u = { 0.9 0.9 0.9 0.9 0.9 0.9 0.9};
rowsense = {'E','E','E'};
cntl= -1;
call lpsolve (rc,objv,solution,dual,rd,object,coef,b,cntl,rowsense,,l,u);
print  solution ;
quit;

Xia Keshan

[Rick_SAS]

This seems to be a completely appropriate question for the IML forum.

[Ksharp]

Hope so . Rick . 

[KGeorge]

Thanks Rick and Xia.

Rick, Indeed I meant that the new probabilities would give rise to the same variance.

Xia, the solution you provide is what I needed for part 1 of my question (which is to obtain E(X)=5.5). I modified your code to include the sampling for the two groups. Many thanks.

However, for part 2 of my question, if for example, E(X) should become 6.867 (which would be a shift upwards of 0.75), the lpsolve call returns 0's for the solution. I think this is because the desired E(X)=6.867 is too close to the maximum score (7) inducing boundary problems. Are there any alternatives to dealing with this?

%let seed=123456;

%let samplesize=1000000;

%let delta=0.75; * mean difference or shift ;

proc iml;

p={0.009 0.001  0.036  0.027  0.145  0.309  0.473};

x=1:7;

mean=(p#x)[+];

var=(p#((x-mean)##2))[+];

print mean var;

expectmean=mean + δ * mean shifted by delta ;

v=(x-expectmean)##2; /*calculated var coefficient*/

print expectmean, v[f=best8.];

/*Start Solution*/

object = { 1 1 1 1 1 1 1 };

coef=x//v//object;

print coef;

b = expectmean // var // {1};

l = { 0.00001 0.00001 0.00001 0.00001 0.00001 0.00001 0.00001};

u = { 0.9999 0.9999 0.9999 0.9999 0.9999 0.9999 0.9999};

rowsense = {'E','E','E'};

cntl= -1;

call lpsolve (rc,objv,solution,dual,rd,object,coef,b,cntl,rowsense,,l,u);

print   solution ;

mean2=(solution`#x)[+];

var2=(solution`#((x-mean2)##2))[+];

print mean var mean2 var2;

/* Sampling for the two groups */

call randseed(&seed);

group1 = sample(x, &samplesize, "Replace", p);

group2 = sample(x, &samplesize, "Replace", solution);

print (mean(group1`))[label="Sample mean group 1"]  (var(group1`))[label="Sample Variance Group 1"], 

      (mean(group2`))[label="Sample mean group 2"]  (var(group2`))[label="Sample variance group 2"];

quit;

[Ksharp]

For you second question, I don't understand "considering boundary limitations towards the last category (X=7)" , you want only change P(x=7) and keep other the same ? But if others have been settled ,then P(x=7) is all settled .

If you only want change E(X) = E(X)+0.3 =6.417, that would be easy .

proc iml;

p={0.009 0.001  0.036  0.027  0.145  0.309  0.473};

x=1:7;

mean=(p#x)[+] ;

var=(p#((x-mean)##2))[+];

print mean var;

v=(x-6.417 /*Delta is 0.3*/)##2; /*calculated var coefficient*/

print v[f=best8.];

/*Start Solution*/

object = { 1 1 1 1 1 1 1 };

coef = {1 2 3 4 5 6 7}//v//{1 1 1 1 1 1 1};

b = { 6.417 /*Delta is 0.3*/}//var//{1};

l = { 0.01 0.01 0.01 0.01 0.01 0.01 0.01};

u = { 0.9 0.9 0.9 0.9 0.9 0.9 0.9};

rowsense = {'E','E','E'};

cntl= -1;

call lpsolve (rc,objv,solution,dual,rd,object,coef,b,cntl,rowsense,,l,u);

print  solution ;

mean=(solution`#x)[+] ;

var=(solution`#((x-mean)##2))[+];

print mean var;

quit;

Xia Keshan

[KGeorge]

Hi Xia Keshan!

Indeed, everything works well when newExpectedValue=E(X) + delta as long as delta is less than or equal to 0.66 (leading to newExpectedValue=6.77). The second question is simply a need to shift E(X) from 6.11 to 6.86 (delta=0.75).

[Ksharp]

if E(X) should become 6.867, I am kind of get feeling LPSOLVE() can't do that , unless sum of p could greater than 1.

or you could post it at OR forum , and see if somebody have a better method .

[KGeorge]

Lots of thanks though!

[Ksharp]

Hi. If you allow a little offset , you could try this:

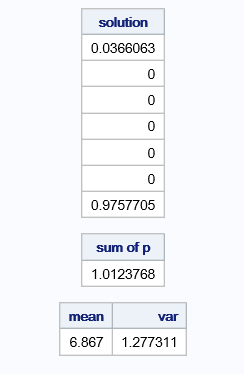
proc iml;
p={0.009 0.001  0.036  0.027  0.145  0.309  0.473};
x=1:7;
mean=(p#x)[+] ; 
var=(p#((x-mean)##2))[+];
print mean var;

 
v=(x-6.867)##2; /*calculated var coefficient*/
print v[f=best8.];



/*Start Solution*/

object = { 0 0 0 0 0 0 0 };
coef = {1 2 3 4 5 6 7}//v//{1 1 1 1 1 1 1};
b = { 6.867}//var//{1};
l = {0 0 0 0 0 0 0 };
u = {1 1 1 1 1 1 1 };
rowsense = {'E','E','G'} ;
cntl= -1;
call lpsolve (rc,objv,solution,dual,rd,object,coef,b,cntl,rowsense,,l,u);
print  solution ,(solution[+])[label='sum of p'];
mean=(solution`#x)[+] ; 
var=(solution`#((x-mean)##2))[+];
print mean var;
quit;

Xia Keshan

[KGeorge]

Hi Xia,

I would prefer not to have an offset. But am so thankful for your efforts.