- Home
- /
- Analytics
- /
- Forecasting
- /
- ARIMA-transfer function
- RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
- Mark as New
- Bookmark
- Subscribe
- Mute
- RSS Feed
- Permalink
- Report Inappropriate Content
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- RSS Feed
- Permalink
- Report Inappropriate Content
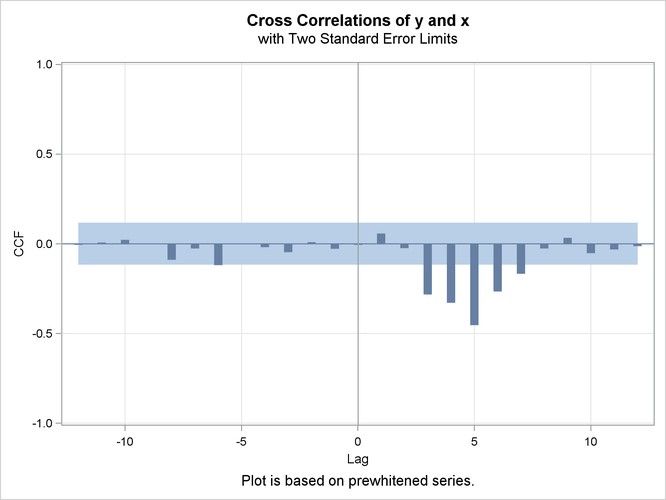
Begin your reference from lag 0.
There are three intervals at lags 0, 1, and 2 before the first significant spike ---> shift=3
A two spike build up at lags 4 and 5 following the first significant spike ---> numerator=1,2
After lag 5, there is decaying significance ---> denominator=1
If there was no decay (an immediate drop to non-significance after lag 5) ---> denominator=0
Your estimate statement in PROC ARIMA should look something like:
estimate input=(3$(1 2)/(1)X) method=ml; run;
Once fit, evaluate the residuals for appropriate AR and MA orders and re-estimate if necessary to obtain WN residuals.
- Mark as New
- Bookmark
- Subscribe
- Mute
- RSS Feed
- Permalink
- Report Inappropriate Content
Begin your reference from lag 0.
There are three intervals at lags 0, 1, and 2 before the first significant spike ---> shift=3
A two spike build up at lags 4 and 5 following the first significant spike ---> numerator=1,2
After lag 5, there is decaying significance ---> denominator=1
If there was no decay (an immediate drop to non-significance after lag 5) ---> denominator=0
Your estimate statement in PROC ARIMA should look something like:
estimate input=(3$(1 2)/(1)X) method=ml; run;
Once fit, evaluate the residuals for appropriate AR and MA orders and re-estimate if necessary to obtain WN residuals.
- Mark as New
- Bookmark
- Subscribe
- Mute
- RSS Feed
- Permalink
- Report Inappropriate Content
- Mark as New
- Bookmark
- Subscribe
- Mute
- RSS Feed
- Permalink
- Report Inappropriate Content
No problem, very glad to help.
You asked how to calculate the r-square of an ARIMA model. My first thought is why do you want to calculate r-square?
If you want a goodness-of-fit statistic to evaluate how well your model fits the data, I'd recommend choosing either AIC or SBC instead of r-square.
Unlike r-square that will never decrease as the number of model parameters increases, both AIC and SBC try to ensure the model is parsimonious. AIC and SBC are standard PROC ARIMA output when build a model.
That said, the link below walks through calculating r-square from output in PROC ARIMA.
http://support.sas.com/kb/37/955.html
- Mark as New
- Bookmark
- Subscribe
- Mute
- RSS Feed
- Permalink
- Report Inappropriate Content
- Ask the Expert: The AI Advantage: How SAS Customer Intelligence 360 Solves Real Marketing Challenges | 27-Jan-2026
- DCSUG presents SAS OnDemand for Academics: the Easy Way to Learn SAS For Free for Students, Educator | 27-Jan-2026
- Ask the Expert: How to Supercharge Enterprise Agentic Workflows With SAS Retrieval Agent Manager | 05-Feb-2026
- Ask the Expert - Génération de données synthétiques : innovation et confidentialité | 10-Feb-2026
- Ask the Expert: Implementing a Digital Twin for the Monopoly Board Game Using SAS® Viya® | 12-Feb-2026
- SAS CI360 Tips and Tricks: Quick Wins, Shortcuts and Hidden Features Every Marketer Should Know | 17-Feb-2026
- SAS Bowl LIX, Integrating SAS and Git | 18-Feb-2026

