PROC GENMOD: p-values are inconsistent in the output

[JamesLin]

Hello:

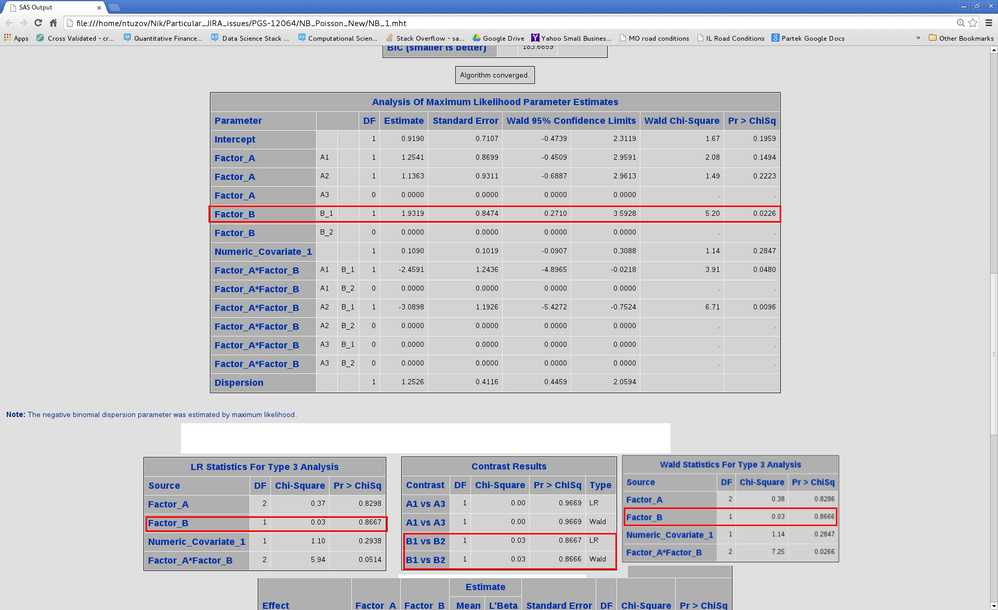
Please help me sort out this output of Negative Binomial regression in PROC GENMOD. The model includes a binary factor, Factor_B. There are a few p-values associated with Factor_B that I expect to be consistent (see the attachment):

1) In “Analysis of Maximum Likelihood estimates” Wald p-value for the corresponding regression coefficient (0.0226)

2) LR test, Type 3, (0.8667)

3) Wald test, Type 3, (0.8666)

4) Contrast “B1 vs B2”, LR (0.8667)

5) Contrast “B1 vs B2”, Wald (0.8666)

As you can see, 1) seems to be a problem. Why is it so different? Note also that the problem showed up only after I fitted the model with Factor_A*Factor_B interaction. In the additive version, everything was consistent.

[JacobSimonsen]

I think the problem is related to the interaction term "Factor_A*Factor_B". It is not meaningfull to test away the maineffect of Factor_B effect when the interactionterm between Factor_A and Factor_B is included in the model.

Will the problem persist if you remove the interactionterm?

[JamesLin]

As I said, there is no problem in the additive version. As for "meaningfulness", it's absolutely beside the point.

[lvm · Accepted solution]

This has been dealt with in a somewhat different (and more complex) context recently.

This is not related to the procedure, but to the nature of the GLM parameterization being used. Wiith interaction, the global test for a main effect involves more than just the main effect parameter.

[JamesLin]

Thank you.  The way I see it is as follows:

1) The Wald/LR Type 3 tests and Wald/LR Contrasts aim at testing whether the mean response is the same in the corresponding cells, B1 and B2 in this case.  LSMEANS statement is of a similar nature.

All these tools are dependent on GLM parameterization so much so that LSMEANS provides no output when reference parameterization is used.

2) Because there is interaction, the mean response depends not only on the main effects of B but also on the A*B interaction effects.  On the other hand, the main table provides Wald p-values just for the main effects of B, i.e. it tests a different hypothesis.

3) It may be possible to remove the discrepancy by switching to reference parametrization, but then the interpretation of 1) as a test for the equality of mean responses will be lost.

[lvm]

You don't want to switch to reference parameterization, unless you want this for other purposes. Interpretation of the global tests becomes really strained when there is an interaction in the model.

[SteveDenham]

I think 'strained' is putting it mildly.  In my opinion, there was a reason Goodnight and Sarle developed the non-full rank parameterization: in agricultural field studies, interactions are the rule rather than the exception, and you just can't get good global tests with full rank parameterizations (see Speed and Hocking for examples).

Steve Denham