How to handle a too wide range of 95% Confidence Intervals?

[afgdurrani0]

Hi,
The mean value of parameters very adequately represents all data and provides the best curve fit to individual data when plotting as x and y. How to handle the wide 95% CI when the mean value best represents the data? Please kindly check the attached SAS report and have a look at parameter TU.

 https://drive.google.com/file/d/1Mu1IrRSC__wRVrG6d5sz73Ktw2POlBFB/view?usp=sharing 

Many thanks for the help and expertise 🙂

[PaigeMiller · Accepted solution]

It tells you the uncertainty around the estimate of the coefficient for TU. Although, the coefficient for TU is still significantly different than zero.

I don't agree that the confidence interval is "too wide" from a statistical point of view, the data is saying there is this much uncertainty around the estimate. It is what the data says it is. It may be "too wide" from a subjective point of view.

[afgdurrani0]

Thanks for the comments. Actually I need a 95% CI close to the mean value. The mean value adequately represent all data without any issues with fitness to data.

[afgdurrani0]

Also the wide range 95%CI issue is only with TU.

[PaigeMiller]

---

@afgdurrani0 wrote:
Also the wide range 95%CI issue is only with TU.

---

I don't understand. The confidence interval is what your data says it is.

[PaigeMiller]

---

@afgdurrani0 wrote:
Actually I need a 95% CI close to the mean value.

---

I don't really know what this means. So let me guess ... you want a predicted value at the mean of all your x-values, and you also want a confidence interval for this predicted value.

[afgdurrani0]

TU along with A and B represent the temperature, C body size on X (time) and Y (meal). TU is actually temperature and the rate of digestion will get zero at TU (22.8 C).

[PaigeMiller]

---

@afgdurrani0 wrote:
TU along with A and B represent the temperature, C body size on X (time) and Y (meal). TU is actually temperature and the rate of digestion will get zero at TU (22.8 C).

---

Honestly, I'm lost, and I don't see how the above relates to the questions you have previously asked, and I don't see how the above relates to my answers.

[afgdurrani0]

Dear Miller, thanks for the comments.
I estimated up to five parameters from my data and only single parameter TU had a wide range of 95% CI which probably be due to small sample size. I am looking for a statistical method that could overcome this issue (small sample size) and provide more precious results for TU with narrow range of 95% CI.

[PaigeMiller]

---

@afgdurrani0 wrote:
I am looking for a statistical method that could overcome this issue (small sample size) and provide more precious results for TU with narrow range of 95% CI.

---

Larger sample size. Otherwise, your confidence interval is what you see. It is what the data says it is.

You keep implying that the confidence interval for TU is too large, I do not agree. You never state "too large" for what.

[PGStats]

The problem is with the strong negative correlation between estimates for TU and B. Which means that you could get a fit that is almost as good to your data by increasing TU and decreasing B, or vice versa. The usual solution to such a problem is to reparameterize your model. For example, you could try replacing EXP(B*(temp-TU)) with EXP(B*temp-BTU), and see if that reduces the correlations.

[afgdurrani0]

Thanks for the comments. The "EXP(B*temp-BTU)" did not run and give this error: ERROR: The variable BTU was referenced but not given a value. Then I slightly modify as EXP(B*temp-B*TU). But the 95% CL gets further larger (-169.3 and 224.5) with this modification.

[PGStats]

In the example I provided, BTU is a new parameter that must be named in the PARMS statement instead of TU (PARMS ... BTU=10 ...).

But this is only an example, the proper parameterisation may require some trial and error.

[afgdurrani0]

@PGStats I revised the code like this: 

proc nlin data=exp method=marquardt;
parms RLT=0.0022 A=0.08 B=0.46 C=1.4 BTU=10;
R=RLT*predlcm**C*EXP(A*temp)*(1-EXP(B*temp-BTU));
model sqrtstw=sqrtsow-0.5*R*time;
output out=expp p=psqrtstw r=stw_residual;
run;

 

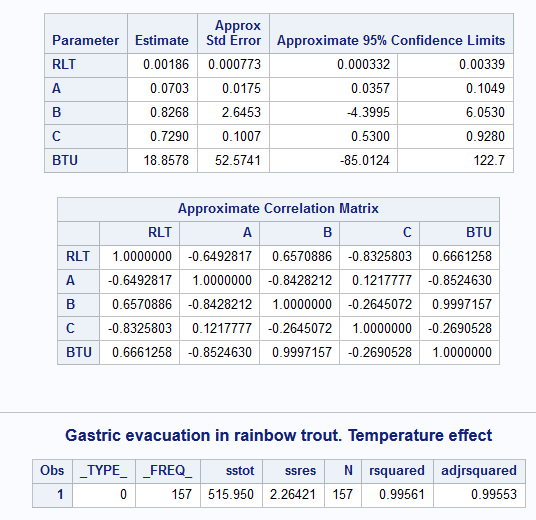
The values get further increased. 

[ballardw]

---

@afgdurrani0 wrote:
Dear Miller, thanks for the comments.
I estimated up to five parameters from my data and only single parameter TU had a wide range of 95% CI which probably be due to small sample size. I am looking for a statistical method that could overcome this issue (small sample size) and provide more precious results for TU with narrow range of 95% CI.

---

I really hope you meant "precise" instead of "precious".