- Home
- /
- Analytics
- /
- Stat Procs
- /
- How to analyze the data for measuring multiply site from same patients...
- RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
- Mark as New
- Bookmark
- Subscribe
- Mute
- RSS Feed
- Permalink
- Report Inappropriate Content
I am doing a study to evaluate the effect of ossification ligament on thoracic vertebra.
The purpose was to explore whether the evoked potentials is different between compressed area and uncompressed area in thoracic vertebra for patients. We collect 6 patients and divide their thoracic vertebra for compressed area and uncompressed area by MRI, respectively.
Then we examine the evoked potential for the thoracic vertebra.
For each patient, we choose five sites to detect the evoked potentials in the compressed area, and five sites to detect the evoked potentials in the uncompressed area too.
Therefore, here's the form of my data (Table1).
How to analyze our data for comparing the difference between compressed area and uncompressed area in thoracic vertebra for patients?
Firstly, we calculated the average for compressed area (site1~site5) and the average for uncompressed area (site1~site5) for each patient, respectively.
So, we compared the average between two groups (compressed area vs. uncompressed area) by paired t tests. However, is it correct way?
Actually, I am confused by the question:
In the current study, we measured the evoked potential in 5 sites for compressed area, and 5 sites for uncompressed area for one patient, respectively.
Could we consider this data as repeated measurement data? The sites were considered as repeated measures factor?
If this is a repeated measures design,how to analyze it?
Repeated Measures Analysis of Variance (ANOVA)?
Moreover, if the data was considered as repeated measured data and we have data missing in the dataset, which method should we choose for the study?
Mixed linear model, Generalized estimating equation or Generalized linear mixed effects model?
For example (Table 2):
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- RSS Feed
- Permalink
- Report Inappropriate Content
If you came to me for an analysis, I would consider this to be a linear mixed model problem, with repeated measures.
To analyze this you would need to get your data into a long format, with a single response value for each record, along with the design factors: ID, treatment (compressed/uncompressed) and site. Possible code would look something like (data is simulated to look something like what you have in Table 1):
data one;
call streaminit(12345);
do i=1 to 2;
do j=1 to 5;
do k=1 to 6;
if i=1 then do;
trt='Uncompressed';
site=j;
result=7 + rand('normal',0,2);
end;
else do;
trt='Compressed';
site=j+5;
result=9 + rand('normal',0,1);
end;
id=k;
output;
end;
end;
end;
run;
proc glimmix data=one;
class trt id site;
model result=trt site*trt/solution ddfm=bw;
random site/residual subject=id(trt) type=cs;
lsmeans trt/diff;
lsmeans trt*site;
run;
The method you propose will certainly work:
Firstly, we calculated the average for compressed area (site1~site5) and the average for uncompressed area (site1~site5) for each patient, respectively.
So, we compared the average between two groups (compressed area vs. uncompressed area) by paired t tests. However, is it correct way?
suspect that the p value for the F test for treatment will be very nearly the same as the p value for the paired t.
One issue is that the sites within each treatment are not truly repeated (that is, site 1 in the compressed area is not site 1 in the uncompressed area). I would recommend renumbering the sites in one of the areas as 6 to 10. Consequently, the model should not contain a main effect for site, in order to prevent non-estimability for the treatment least squares means.
Regarding the missing values question, the mixed model procedures are robust to these so long as the data are missing at random, which is a reasonable assumption.
Here is code in case you want to try a generalized estimating approach. Note that the standard error is smaller.
proc genmod data=one;
class trt id site;
model result=trt trt*site/type3;
repeated subject=id*site/type=exch;
lsmeans trt/diff;
lsmeans trt*site;
run;Treatment means are the same.
SteveDenham
- Mark as New
- Bookmark
- Subscribe
- Mute
- RSS Feed
- Permalink
- Report Inappropriate Content
If you came to me for an analysis, I would consider this to be a linear mixed model problem, with repeated measures.
To analyze this you would need to get your data into a long format, with a single response value for each record, along with the design factors: ID, treatment (compressed/uncompressed) and site. Possible code would look something like (data is simulated to look something like what you have in Table 1):
data one;
call streaminit(12345);
do i=1 to 2;
do j=1 to 5;
do k=1 to 6;
if i=1 then do;
trt='Uncompressed';
site=j;
result=7 + rand('normal',0,2);
end;
else do;
trt='Compressed';
site=j+5;
result=9 + rand('normal',0,1);
end;
id=k;
output;
end;
end;
end;
run;
proc glimmix data=one;
class trt id site;
model result=trt site*trt/solution ddfm=bw;
random site/residual subject=id(trt) type=cs;
lsmeans trt/diff;
lsmeans trt*site;
run;
The method you propose will certainly work:
Firstly, we calculated the average for compressed area (site1~site5) and the average for uncompressed area (site1~site5) for each patient, respectively.
So, we compared the average between two groups (compressed area vs. uncompressed area) by paired t tests. However, is it correct way?
suspect that the p value for the F test for treatment will be very nearly the same as the p value for the paired t.
One issue is that the sites within each treatment are not truly repeated (that is, site 1 in the compressed area is not site 1 in the uncompressed area). I would recommend renumbering the sites in one of the areas as 6 to 10. Consequently, the model should not contain a main effect for site, in order to prevent non-estimability for the treatment least squares means.
Regarding the missing values question, the mixed model procedures are robust to these so long as the data are missing at random, which is a reasonable assumption.
Here is code in case you want to try a generalized estimating approach. Note that the standard error is smaller.
proc genmod data=one;
class trt id site;
model result=trt trt*site/type3;
repeated subject=id*site/type=exch;
lsmeans trt/diff;
lsmeans trt*site;
run;Treatment means are the same.
SteveDenham
- Mark as New
- Bookmark
- Subscribe
- Mute
- RSS Feed
- Permalink
- Report Inappropriate Content
Dear Prof. SteveDenham
Thank you very much for your extremely generous help.
Fortunately for us, you pointed out the problem that the sites within each treatment are not truly repeated.
Sorry for being unclear.
You suggested that we can compare the average between two groups by paired t tests.
We also could consider this to be a linear mixed model problem, with repeated measures.
Moreover, the procedure of “proc glimmix” and “proc genmod” was provided to analysis the repeated measurement data .
Your suggestions are very valuable and precious for us.
Could we also conduct the analysis by the procedure of “proc mixed” ?
What are the repeated measurement factors in this study?
Many thanks!
Best regards
- Mark as New
- Bookmark
- Subscribe
- Mute
- RSS Feed
- Permalink
- Report Inappropriate Content
Here is a version using PROC MIXED. It yields the same results as the PROC GLIMMIX code.
proc mixed data=one;
class trt id site;
model result=trt site*trt/solution ddfm=bw;
repeated site/ subject=id(trt) type=cs;
lsmeans trt/diff;
lsmeans trt*site;
run;SteveDenham
- Mark as New
- Bookmark
- Subscribe
- Mute
- RSS Feed
- Permalink
- Report Inappropriate Content
Best regards!
- Mark as New
- Bookmark
- Subscribe
- Mute
- RSS Feed
- Permalink
- Report Inappropriate Content
Hello @Dennisky,
Glad to see that @SteveDenham's solution worked for you. Then it would be fair and help later readers if you marked his most helpful reply as the accepted solution, not your own "thank you" post. Could you please change that? It's very easy: Select his post as the solution after clicking "Not the Solution" in the option menu (see icon below) of the current solution.
- Mark as New
- Bookmark
- Subscribe
- Mute
- RSS Feed
- Permalink
- Report Inappropriate Content
Best regards!
- Mark as New
- Bookmark
- Subscribe
- Mute
- RSS Feed
- Permalink
- Report Inappropriate Content
Dear Prof. SteveDenham,
A few months ago,we want to analyze our data for measuring multiply site from same patients.
You taught us to conduct the study by using GLMM and GEE approach. Thank you very much for your generous help.
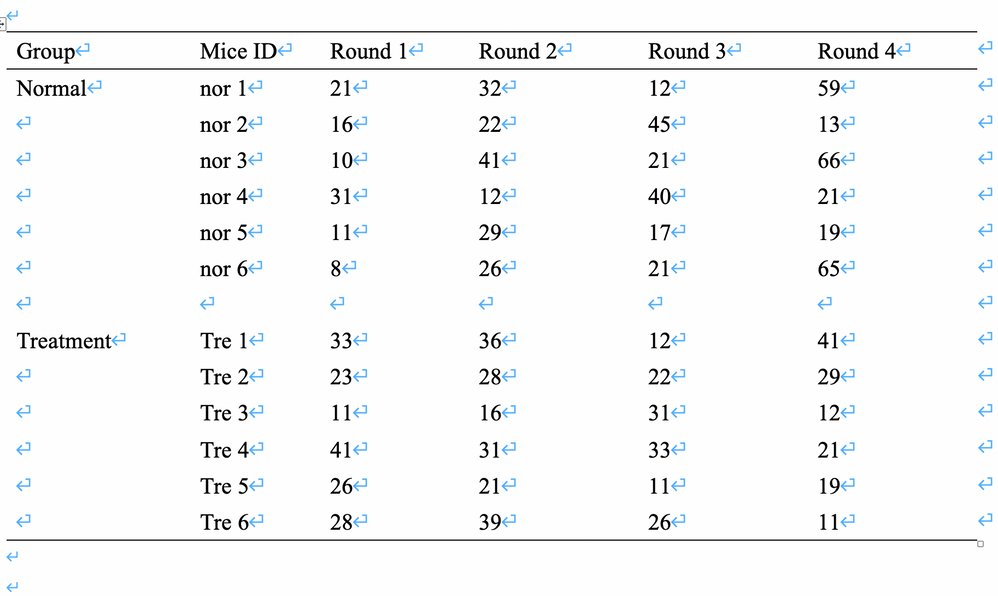
Now, we want to compare the difference of the data from Gait Analysis between normal group and treatment group in mice.
There are 6 mice in the normal group and treatment group, respectively. We plan to conduct all mice pass the machine of Shuttle-Box for Gait Analysis one by one. Due to the data varied widely from itself, we arrange each mice passes the Shuttle-Box four times (round1~round4).
Why the data varied widely? We suspect that the emotional state of mice may play a role in the results. Mice are naturally very timid and shy animals. The result of gait analysis might be influenced by even mild stimulus. Thus, the data was much different every round (round1~round4) for each mice.
So, how to analyze the data for this study?
1、Firstly, we calculated the average for each mice (round1~round4) in normal group and the average for each mice (round1~round4) in treatment group, respectively. We compared the average between two groups by t tests.
2、Alternatively, could the study also be considered as repeated measure design? And we conduct the study by using GLMM or GEE approach. However, in the study, we arrange each mice passes the Shuttle-Box four times (round1~round4).
Is it different from the traditional time factor for repeated measure study? (Such as, the patients take a new antihypertensive drug, we measured their blood pressure at 7days, 14days, 21days, 28days).
Which method should we choose for the present study?
Please forgive us for disturbing you.
Thank you very much for your help!
Best regards
Dennis Wang
ANOVA, or Analysis Of Variance, is used to compare the averages or means of two or more populations to better understand how they differ. Watch this tutorial for more.
Find more tutorials on the SAS Users YouTube channel.