- Home
- /
- Analytics
- /
- Stat Procs
- /
- Continous outcome variable and Categorical independent variable
- RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
- Mark as New
- Bookmark
- Subscribe
- Mute
- RSS Feed
- Permalink
- Report Inappropriate Content
My project involves finding the difference in total length of stay in days (continuous variable) in hospital among 5 groups of patients divided based on their body temperature (Categorical variable with 5 categories). Total length of stay is not normally distributed. One option is for me to do non-parametric Wilcox Mann-Whitney test. But this will not allow me to adjust for a=other potential confounders. Is there any other procedure which will allow me to find a median difference in total length of stay between those 5 groups after adjusting for potential confounders.
I would appreciate any help I can get on this. Thanks.
- Mark as New
- Bookmark
- Subscribe
- Mute
- RSS Feed
- Permalink
- Report Inappropriate Content
You mean the non-parameter version ANOVA ?
Check proc freq 's CMH statistics . and Example : Friedman’s Chi-Square Test
Xia Keshan
- Mark as New
- Bookmark
- Subscribe
- Mute
- RSS Feed
- Permalink
- Report Inappropriate Content
First, the dependent variable does not need to be normally distributed. The errors from the model (as estimated by the residuals) need to be normally distributed. However, from your description, it is likely that the residuals are also non-normal. Second, your outcome variable is not nominal, it is continuous (length of stay)
If that is the case, then there are several options.
1) You could try transforming the DV or the IVs.
2) You could use robust statistics.
Just a couple days ago I presented a paper at SGF entitled "Alternative methods of regression when OLS is not right".
- Mark as New
- Bookmark
- Subscribe
- Mute
- RSS Feed
- Permalink
- Report Inappropriate Content
In addition to Peter's methods, you may want to consider this to be a Cox proportional hazards regression, with time to exit from hospital as a left-truncated/right censored variable, and fit it as in Example 73.3 Modeling with Categorical Predictors in the SAS/STAT13.2 documentation for PROC PHREG.
Steve Denham
- Mark as New
- Bookmark
- Subscribe
- Mute
- RSS Feed
- Permalink
- Report Inappropriate Content
That is a good idea, Steve, particularly if there is censoring (which isn't clear from the original post)
- Mark as New
- Bookmark
- Subscribe
- Mute
- RSS Feed
- Permalink
- Report Inappropriate Content
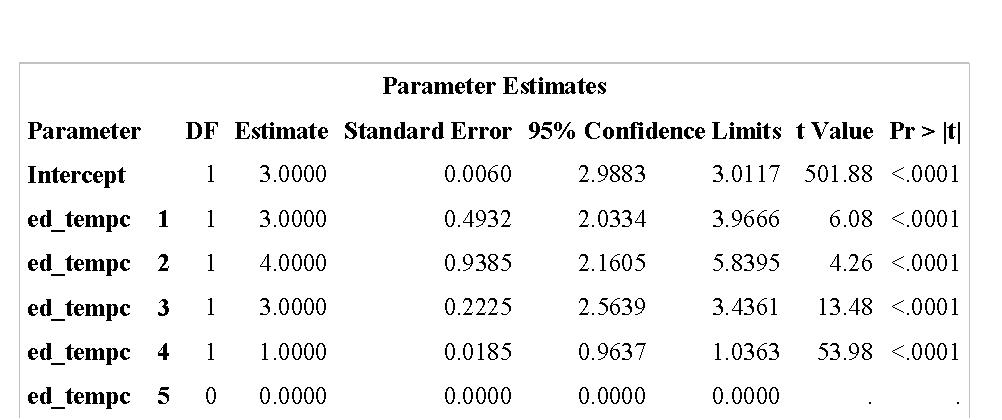
Thank you for your response. I went through your article and carried out quantile regression. My dependent variable is continuous and measured as total length of stay in hospital in days. Independent variable is body temperature divided into five categorical groups. The image of the table is above.
I am little confused about how to interpret the result. The 95% CI for the parameter estimates is not significant for the ed_tempc group 4, but p value is
<0.0001. How do I interpret this?
I chose the quantile as median.
Also, looking at the result, can I say that: As compared to group 5 of ed_tempc (which is a reference group), the median length of stay for
group 1 is 3 days more (95% CI 2.03-3.96). Am I interpreting it right???
April 27 – 30 | Gaylord Texan | Grapevine, Texas
Registration is open
Walk in ready to learn. Walk out ready to deliver. This is the data and AI conference you can't afford to miss.
Register now and lock in 2025 pricing—just $495!
ANOVA, or Analysis Of Variance, is used to compare the averages or means of two or more populations to better understand how they differ. Watch this tutorial for more.
Find more tutorials on the SAS Users YouTube channel.




