PROC FMM with two overlapping distributions

[BobHope]

Hi,

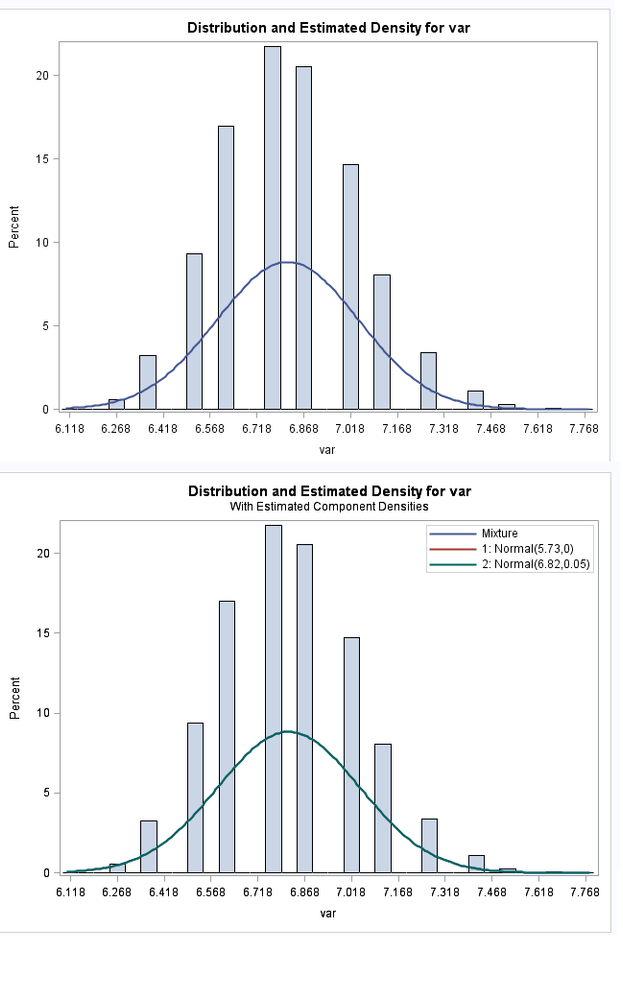
I have data which constructs from two normal distributions (know property). And I am trying to find an estimate for the parameters of those distributions. I have been using proc FMM which works greatly if the two distributions are separatable by eye. However problems arise when the two distributions are close to each other. I understand that this might be a problem, but is there a way to force FMM to assume that when there is only one distribution to the eye, then it would try to find the distribution that should be mulitplied by 2 to get the distribution the data suggests? I have attached two output graphs which are from the FMM with k=1 and k=2 respectively. For some reason the K=2 finds a nonexisting distribution with mean of 5.73 and variance of 0??? I am using SAS 9.4

[Rick_SAS · Accepted solution]

I've written about some of these issues on my blog. Main takeways: if you have small samples, it might not be possible. However, the PROC FMM syntax enables you to specify "hints" about the number of components and even about which observations might belong to each component. So if you have domain knowledge you might be able to specify the PARTIAL= option or the PARMS statement and help PROC FMM determine the components.

[BobHope]

Thank you for the answer. Indeed this method is possible but it was not that straight forward in my case. Got to say FMM is a great proc.