SAS-IML complex optimization problem/ Huber regression: Returning from module FF without return

[Ksharp]

Better post it at IML forum. @Rick_SAS is there. 

Hope I have time to review your question .

Good Luck.

[kilasue]

I rewrite the objective function using do:

nr=nrow(A);	
start ff(x) global(A,y,lambda,l,nr);
	xx=x[1:l-1];
	sigma=x[l];
	f=0;
	do i=1 to nr;
	  f=f+sigma+huberf((A[i,]*xx-y[i])/sigma)*sigma;
	end;
	f=f+lambda*norm(x,"L2");
	return(f);
finish ff;

But I still can understand why my previous function caused an error. Maybe we cannot using apply() in objective function?

[kilasue]

Recently I see that sicikitlearn has a Huberregressor and I want to implement it using SAS. The loss function is in the picture:

My code is:

proc iml;
	use mach.leaf_cla;
	read all var _all_ into data[colname=varNames]; 
	
	A=data[,1:ncol(data)-1];
	y=data[,ncol(data)];
	cv=j(nrow(A), 1, 1);
	A=insert(A,cv,0,ncol(A)+1);

	*Using OLS estimator as the start value;
	b=solve(A`*A,A`*y);
	*Hm(x);
	start huberf(x) global(epsilon);
		if abs(x)<epsilon then f=x**2;
		else f=2*epsilon*abs(x)-epsilon**2;

		return(f);
	finish huberf;

	*Objective function;
	start ff(x) global(A,y,lambda,l);
		xx=x[1:l-1];
		sigma=x[l];
		AX=(A*xx-y)/sigma;
		AXt=apply("huberf",AX);
		
		f=sum(sigma+AXt*sigma)+lambda*norm(x,"L2");
		return(f);
	finish ff;

	epsilon=1.35;
	lambda=1;
	l=ncol(A)+1;
	opt={0 2};
	sigma=50;
	b=insert(b,sigma,nrow(b)+1,0);
	temp=ff(b);
	print temp;
	call nlpnrr(rc, xres, "ff", b, opt);

My dataset is in the attachments.

But nlprr gives an error:

I have tried nlpcg, nlpdd and nothing works. It's strange that I have tried ff(b) using start value and it give correct result.

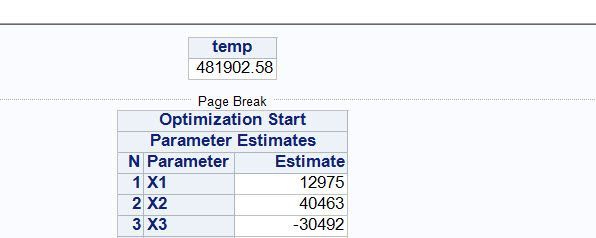
More details:

 The dataset has 64 explanatory variables and 1 target variable. The model has 64+1 constant +1 sigma =66 parameters.

[Rick_SAS]

I suspect you are correct that the APPLY function is causing the problem, although I don't know why. I will enter a bug report with SAS R&D so that someone can investigate.

An efficient alternative is to use the CHOOSE function. The APPLY function is not recommended because the APPLY function tends to be less efficient than vectorized computations.

In your case, you can avoid the loop by using the following:

start huberf(x) global(epsilon);
   f = choose( abs(x)<epsilon, x##2, 2*epsilon*abs(x)-epsilon##2 );
   return(f);
finish huberf;

PS. In your objective function, I think you meant to write NORM(xx) instead of NORM(x)?