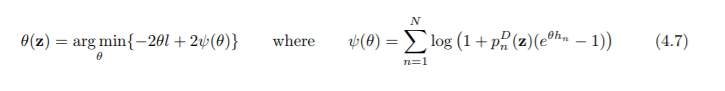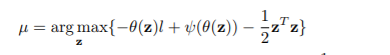- RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
- Mark as New
- Bookmark
- Subscribe
- Mute
- RSS Feed
- Permalink
- Report Inappropriate Content
Hi,
I'm trying to solve a nested optimization problem with SAS/IML, specifically):
I'm not sure how to handle the input vs global variables in this case (which I think is why it is not working). I don't know how to handle z. This is what i have so far:
/* function P*/
start P(z) global(h,b,p1,p2,a_inter,X_I);
return( sum(h#(CDF('NORMAL',(b-p1#(X_I*(a_inter*(z`))))/p2))) );
finish;
/* derivative of theta function*/
start deri(theta_x) global(l,h,z);
return( l - sum(P(z)#h#exp(h*theta_x)/( P(z)#(exp(h*theta_x)-1) + 1 ) ) );
finish;
/* finding root of theta function*/
start theta(z);
bounds = {0,10000};
return( froot( "deri", bounds) );
finish;
/*main function*/
start Func(z) global(l,h);
return( -theta(z)*l + (sum(log(1 + P(z)#(exp(h#theta(z)) - 1) ) )) - 0.5*z*(z`) );
finish;
z = RANDNORMAL(S,0, 1); /*x0*/
z = (z`);
opt = {1,2};
call nlpnra(rc, result, "Func", z, opt);
Given that the equations are done correctly, how would I set this up so that the root/derivative function can make use if the current z that the optimization algorithm is evaluating? Is there something else that is wrong?
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- RSS Feed
- Permalink
- Report Inappropriate Content
You haven't defined S, l, or h.
I suggest you start by reading the article "Ten tips before you run an optimization." You also might want to look at "Optimizing a function of an integral," which optimizes a function that in turn calls other functions.
- Mark as New
- Bookmark
- Subscribe
- Mute
- RSS Feed
- Permalink
- Report Inappropriate Content
You haven't defined S, l, or h.
I suggest you start by reading the article "Ten tips before you run an optimization." You also might want to look at "Optimizing a function of an integral," which optimizes a function that in turn calls other functions.
- Mark as New
- Bookmark
- Subscribe
- Mute
- RSS Feed
- Permalink
- Report Inappropriate Content
I should have shown the step where i define them, my bad. (They are all vectors of length 1xN)
I'll start reading up on what you linked me, thank you!
- Mark as New
- Bookmark
- Subscribe
- Mute
- RSS Feed
- Permalink
- Report Inappropriate Content
Haven't looked through your functions in depth, but have have a few parameters, which you have not defined yet. Eg S and I.
Also, why do you set z = (z`) ?
- Mark as New
- Bookmark
- Subscribe
- Mute
- RSS Feed
- Permalink
- Report Inappropriate Content
Sorry for the confusion, i should have shown the step where I import the other variables, all of them are defined vectors (1xN)
When trying the function one by one it seemed as z was transposed when i sent it in so i just did that as a quick fix.
April 27 – 30 | Gaylord Texan | Grapevine, Texas
Registration is open
Walk in ready to learn. Walk out ready to deliver. This is the data and AI conference you can't afford to miss.
Register now and save with the early bird rate—just $795!
- SAS Bowl LVIII, SAS Viya Copilot | 21-Jan-2026
- Ask the Expert: Wie der SAS Visual Analytics Copilot Ihre Arbeit beschleunigt! | 22-Jan-2026
- Ask the Expert: The AI Advantage: How SAS Customer Intelligence 360 Solves Real Marketing Challenges | 27-Jan-2026
- DCSUG presents SAS OnDemand for Academics: the Easy Way to Learn SAS For Free for Students, Educator | 27-Jan-2026
- Ask the Expert: How to Supercharge Enterprise Agentic Workflows With SAS Retrieval Agent Manager | 05-Feb-2026
- Ask the Expert: Implementing a Digital Twin for the Monopoly Board Game Using SAS® Viya® | 12-Feb-2026
- SAS CI360 Tips and Tricks: Quick Wins, Shortcuts and Hidden Features Every Marketer Should Know | 17-Feb-2026