- RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
- Mark as New
- Bookmark
- Subscribe
- Mute
- RSS Feed
- Permalink
- Report Inappropriate Content
I am using SAS to solve a nonlinear problem.
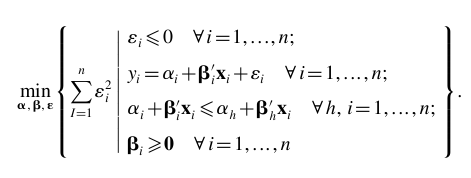
I once tried "solve with QP", but the calculated result is wrong. (I use matlab fmincon to solve the same problem, and the two results are different. The matlab result is much more convincing, and I believe the result given by matlab is correct). However, when I tried "solve;" in my code, the SAS just can not solve it. In the note, it indicated that The SAS System stopped processing this step because of errors. Can someone help me check my code? Thanks so much.
data data_read;
input x1 x2 y1 dmu_id;
datalines;
20.22 1 85 1
95.51 1 25 2
1662.98 5 22 3
;
/*---------solve QP--------*/
proc optmodel printlevel=0;
set x_num=1..2; * set dimension of X ;
set y_num=1..1;
set <num>DMU_ID;
num X{DMU_ID,x_num};
num Y{DMU_ID,y_num};
read data data_read into DMU_ID=[dmu_id]
{r in x_num}<X[dmu_id,r]=col("x"||r)>
{s in y_num}<Y[dmu_id,s]=col("y"||s)>;
var epi{DMU_ID}>=0;
var alpha{DMU_ID};
var beta{DMU_ID,x_num}>=0;
num epi_sol{DMU_ID};
num alpha_sol{DMU_ID};
num beta_sol{DMU_ID,x_num};
min obj=sum{q in DMU_ID}epi**2;
con regression{q in DMU_ID,s in y_num}:Y[q,s]=alpha-epi
+sum{r in x_num}X[q,r]*beta[q,r];
con concave{q in DMU_ID,h in DMU_ID}:alpha+sum{r in x_num}X[q,r]*beta[q,r]<=alpha
solve;
for{q in DMU_ID}epi_sol=epi
.sol;
for{q in DMU_ID}alpha_sol=alpha
.sol;
for{q in DMU_ID,r in x_num}beta_sol[q,r]=beta[q,r].sol;
create data epi_sol from [dmu_id]epi_sol;
create data alpha_sol from [dmu_id]alpha_sol;
create data beta_sol from [dmu_id x_num]beta_sol;
quit;
run;
- Mark as New
- Bookmark
- Subscribe
- Mute
- RSS Feed
- Permalink
- Report Inappropriate Content
I can't reproduce the error on SAS 9.3. There are a few minor messages that can be addressed, but no errors. Could you please attach your log file?
Here is what I get:
------
172 data data_read;
173 input x1 x2 y1 dmu_id;
174 datalines;
NOTE: The data set WORK.DATA_READ has 3 observations and 4 variables.
NOTE: DATA statement used (Total process time):
real time 0.00 seconds
cpu time 0.01 seconds
178 ;
179 /*---------solve QP--------*/
180 proc optmodel printlevel=0;
181 set x_num=1..2;
181! * set dimension of X ;
182 set y_num=1..1;
183 set <num>DMU_ID;
184 num X{DMU_ID,x_num};
185 num Y{DMU_ID,y_num};
186 read data data_read into DMU_ID=[dmu_id]
-
777
NOTE 777-782: The name 'dmu_id' hides an outer declaration.
187 {r in x_num} <X[dmu_id,r]=col("x"||r)>
188 {s in y_num} <Y[dmu_id,s]=col("y"||s)>;
NOTE: There were 3 observations read from the data set WORK.DATA_READ.
189
190 var epi{DMU_ID}>=0;
191 var alpha{DMU_ID};
192 var beta{DMU_ID,x_num}>=0;
193
194 min obj= sum{q in DMU_ID} epi**2;
195 con regression{q in DMU_ID,s in y_num}:
196 Y[q,s] = alpha
197 - epi
198 + sum{r in x_num} X[q,r]*beta[q,r];
199 con concave{q in DMU_ID,h in DMU_ID}:
200 alpha + sum{r in x_num} X[q,r]*beta[q,r]
201 <= alpha
202 solve;
NOTE: Problem generation will use 4 threads.
NOTE: The constraint 'concave[1,1]' is empty.
NOTE: The constraint 'concave[2,2]' is empty.
NOTE: The constraint 'concave[3,3]' is empty.
NOTE: The problem has 12 variables (3 free, 0 fixed).
NOTE: The problem has 12 linear constraints (9 LE, 3 EQ, 0 GE, 0 range).
NOTE: The problem has 48 linear constraint coefficients.
NOTE: The problem has 0 nonlinear constraints (0 LE, 0 EQ, 0 GE, 0 range).
NOTE: The OPTMODEL presolver removed 0 variables, 3 linear constraints, and 0 nonlinear
constraints.
NOTE: The OPTMODEL presolved problem has 12 variables, 9 linear constraints, and 0 nonlinear
constraints.
NOTE: The QP presolver value AUTOMATIC is applied.
NOTE: The QP presolver removed 0 variables and 0 constraints.
NOTE: The QP presolver removed 0 constraint coefficients.
NOTE: The presolved problem has 12 variables, 9 constraints, and 48 constraint coefficients.
NOTE: The QP solver is called.
NOTE: The Interior Point algorithm is used.
NOTE: The deterministic parallel mode is enabled.
NOTE: The Interior Point algorithm is using up to 4 threads.
Primal Bound Dual
Iter Complement Duality Gap Infeas Infeas Infeas
0 2.91929e+03 5.84738e-01 5.84520e-01 6.60197e+01 3.94884e+04
1 2.16097e+03 1.42333e+00 3.60634e-01 4.07325e+01 2.43634e+04
2 1.37176e+03 5.09543e+00 7.69786e-02 8.69449e+00 5.20044e+03
3 3.89368e+02 2.27760e+00 2.22052e-02 2.50801e+00 1.50012e+03
4 3.92930e+02 2.51196e+00 2.18544e-02 2.46839e+00 1.47642e+03
5 4.47907e+02 1.21485e+01 2.08696e-02 2.35716e+00 1.40989e+03
6 2.97149e+03 1.80112e-01 1.05151e-02 1.18765e+00 7.10371e+02
7 2.27681e+03 1.25190e-01 7.63588e-03 8.62449e-01 5.15858e+02
8 1.16576e+03 4.90437e-02 3.61949e-03 4.08810e-01 2.44522e+02
9 4.99641e+02 2.16038e-02 1.44582e-03 1.63301e-01 9.76752e+01
10 4.49887e+02 3.53944e-02 1.20773e-03 1.36409e-01 8.15905e+01
11 4.09736e+02 1.85557e-01 1.00743e-03 1.13786e-01 6.80590e+01
12 6.36467e+03 1.65790e-01 5.39117e-04 6.08916e-02 3.64211e+01
13 2.43454e+02 2.21331e-02 8.60910e-06 9.72371e-04 5.81605e-01
14 2.58773e+00 2.46941e-04 8.67933e-08 9.80304e-06 5.86350e-03
15 1.77261e-02 2.46950e-06 7.33576e-07 8.64549e-08 2.56299e-05
16 1.77261e-04 2.46950e-08 7.33576e-09 8.64559e-10 2.56299e-07
17 1.77269e-06 2.46962e-10 7.33592e-11 8.64698e-12 2.56296e-09
18 1.77269e-08 2.47041e-12 7.37477e-13 1.37854e-13 2.59279e-11
NOTE: Optimal.
NOTE: Objective = 7569.
NOTE: The Interior Point solve time is 0.02 seconds.
203
204 *num epi_sol{q in DMU_ID} = epi.sol;
205 num alpha_sol{DMU_ID};
206 num beta_sol{DMU_ID,x_num};
207
208 *for{q in DMU_ID}epi_sol= epi
.sol;
209 for{q in DMU_ID}alpha_sol=alpha
.sol;
210 for{q in DMU_ID,r in x_num}beta_sol[q,r]=beta[q,r].sol;
211 create data epi_sol from [DMU_ID] epi;
NOTE: The data set WORK.EPI_SOL has 3 observations and 2 variables.
212 create data alpha_sol from [DMU_ID]alpha_sol;
NOTE: The data set WORK.ALPHA_SOL has 3 observations and 2 variables.
213 create data beta_sol from [DMU_ID x_num]beta_sol;
NOTE: The data set WORK.BETA_SOL has 6 observations and 3 variables.
214 quit;
NOTE: PROCEDURE OPTMODEL used (Total process time):
real time 0.06 seconds
cpu time 0.06 seconds
------
Thanks,
Leo.
- Mark as New
- Bookmark
- Subscribe
- Mute
- RSS Feed
- Permalink
- Report Inappropriate Content
Thanks so much. I use SAS 9.2 and below is the log file. It seems that my SAS version does have some problem. However, the optimal obj calculated from matlab is zero. I hope to find what is something wrong in my code. Thanks again.
---------------------------------------------------------------------------------------------
385 data data_read;
386 input x1 x2 y1 dmu_id;
387 datalines;
NOTE: The data set WORK.DATA_READ has 3 observations and 4 variables.
NOTE: DATA statement used (Total process time):
real time 0.03 seconds
cpu time 0.01 seconds
391 ;
392 proc optmodel printlevel=0;
393 set x_num=1..2;
393! * set dimension of X ;
394 set y_num=1..1;
395 set <num>DMU_ID;
396 num X{DMU_ID,x_num};
397 num Y{DMU_ID,y_num};
398 read data data_read into DMU_ID=[dmu_id]
399 {r in x_num}<X[dmu_id,r]=col("x"||r)>
400 {s in y_num}<Y[dmu_id,s]=col("y"||s)>;
NOTE: There were 3 observations read from the data set WORK.DATA_READ.
401 var epi{DMU_ID}>=0;
402 var alpha{DMU_ID};
403 var beta{DMU_ID,x_num}>=0;
404 num epi_sol{DMU_ID};
405 num alpha_sol{DMU_ID};
406 num beta_sol{DMU_ID,x_num};
407 min obj=sum{q in DMU_ID}epi**2;
408 con regression{q in DMU_ID,s in y_num}:Y[q,s]=alpha-epi
+sum{r in x_num}X[q,r]*beta[q,r];
409 con concave{q in DMU_ID,h in DMU_ID}:alpha+sum{r in x_num}X[q,r]*beta[q,r]<=alpha
410 solve;
NOTE: The constraint 'concave[1,1]' is empty.
NOTE: The constraint 'concave[2,2]' is empty.
NOTE: The constraint 'concave[3,3]' is empty.
NOTE: The problem has 12 variables (3 free, 0 fixed).
NOTE: The problem has 12 linear constraints (9 LE, 3 EQ, 0 GE, 0 range).
NOTE: The problem has 48 linear constraint coefficients.
NOTE: The problem has 0 nonlinear constraints (0 LE, 0 EQ, 0 GE, 0 range).
NOTE: The OPTMODEL presolver removed 0 variables, 3 linear constraints, and 0 nonlinear constraints.
NOTE: The OPTMODEL presolved problem has 12 variables, 9 linear constraints, and 0 nonlinear constraints.
NOTE: Using analytic derivatives for objective.
NOTE: Initial point was changed to be feasible to bound and linear constraints.
NOTE: The trust region method is used.
NOTE: The SAS System stopped processing this step because of errors.
NOTE: PROCEDURE OPTMODEL used (Total process time):
real time 0.03 seconds
cpu time 0.03 seconds
411 for{q in DMU_ID}epi_sol=epi
.sol;
412 for{q in DMU_ID}alpha_sol=alpha
.sol;
413 for{q in DMU_ID,r in x_num}beta_sol[q,r]=beta[q,r].sol;
414 create data epi_sol from [dmu_id]epi_sol;
415 create data alpha_sol from [dmu_id]alpha_sol;
416 create data beta_sol from [dmu_id x_num]beta_sol;
417 quit;
418 run;
- Mark as New
- Bookmark
- Subscribe
- Mute
- RSS Feed
- Permalink
- Report Inappropriate Content
I am glad to help.
I have forwarded your model to someone who might be able to reproduce your problem.
There are a couple of things that may help further, if you are able to provide them:
1. Your Matlab code
2. The very top of the log file, where the detailed version information is.
Cheers,
Leo.
- Mark as New
- Bookmark
- Subscribe
- Mute
- RSS Feed
- Permalink
- Report Inappropriate Content
Hi Violet,
Our folks suggested that if you can, please upgrade to at least 9.3. This problem does not occur there.
Technical Support may also be able to help: http://support.sas.com/techsup/contact/
Good luck and thanks for sharing!
Leo.
- Mark as New
- Bookmark
- Subscribe
- Mute
- RSS Feed
- Permalink
- Report Inappropriate Content
Thanks. Yes, I should upgrade my SAS version.
- Mark as New
- Bookmark
- Subscribe
- Mute
- RSS Feed
- Permalink
- Report Inappropriate Content
You're welcome!
April 27 – 30 | Gaylord Texan | Grapevine, Texas
Registration is open
Walk in ready to learn. Walk out ready to deliver. This is the data and AI conference you can't afford to miss.
Register now and save with the early bird rate—just $795!
- SAS Bowl LVIII, SAS Viya Copilot | 21-Jan-2026
- Ask the Expert: Wie der SAS Visual Analytics Copilot Ihre Arbeit beschleunigt! | 22-Jan-2026
- Ask the Expert: The AI Advantage: How SAS Customer Intelligence 360 Solves Real Marketing Challenges | 27-Jan-2026
- DCSUG presents SAS OnDemand for Academics: the Easy Way to Learn SAS For Free for Students, Educator | 27-Jan-2026
- Ask the Expert: How to Supercharge Enterprise Agentic Workflows With SAS Retrieval Agent Manager | 05-Feb-2026
- Ask the Expert: Implementing a Digital Twin for the Monopoly Board Game Using SAS® Viya® | 12-Feb-2026
- SAS CI360 Tips and Tricks: Quick Wins, Shortcuts and Hidden Features Every Marketer Should Know | 17-Feb-2026
