Pls help me check this code

[violet2386]

I am using SAS to solve a nonlinear problem.

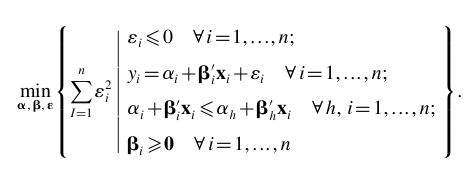
I once tried "solve with QP", but the calculated result is wrong. (I use matlab fmincon to solve the same problem, and the two results are different. The matlab result is much more convincing, and I believe the result given by matlab is correct).  However, when I tried "solve;" in my code, the SAS just can not solve it. In the note, it indicated that The SAS System stopped processing this step because of errors. Can someone help me check my code? Thanks so much.

data data_read;

input x1 x2 y1 dmu_id;

datalines;

20.22 1 85 1

95.51 1 25 2

1662.98 5 22 3

;

/*---------solve QP--------*/

proc optmodel printlevel=0;

set x_num=1..2;    * set dimension of X ;

set y_num=1..1;

set <num>DMU_ID;

num X{DMU_ID,x_num};

num Y{DMU_ID,y_num};

read data data_read into DMU_ID=[dmu_id]

{r in x_num}<X[dmu_id,r]=col("x"||r)>

{s in y_num}<Y[dmu_id,s]=col("y"||s)>;

var epi{DMU_ID}>=0;

var alpha{DMU_ID};

var beta{DMU_ID,x_num}>=0;

num epi_sol{DMU_ID};

num alpha_sol{DMU_ID};

num beta_sol{DMU_ID,x_num};

min obj=sum{q in DMU_ID}epi**2;

con regression{q in DMU_ID,s in y_num}:Y[q,s]=alpha-epi+sum{r in x_num}X[q,r]*beta[q,r];

con concave{q in DMU_ID,h in DMU_ID}:alpha+sum{r in x_num}X[q,r]*beta[q,r]<=alpha+sum{r in x_num}X[q,r]*beta[h,r];

solve;

for{q in DMU_ID}epi_sol=epi.sol;

for{q in DMU_ID}alpha_sol=alpha.sol;

for{q in DMU_ID,r in x_num}beta_sol[q,r]=beta[q,r].sol;

create data epi_sol from [dmu_id]epi_sol;

create data alpha_sol from [dmu_id]alpha_sol;

create data beta_sol from [dmu_id x_num]beta_sol;

quit;

run;

[LeoLopes]

I can't reproduce the error on SAS 9.3. There are a few minor messages that can be addressed, but no errors. Could you please attach your log file?

Here is what I get:

------

172  data data_read;

173  input x1 x2 y1 dmu_id;

174  datalines;

NOTE: The data set WORK.DATA_READ has 3 observations and 4 variables.

NOTE: DATA statement used (Total process time):

      real time           0.00 seconds

      cpu time            0.01 seconds

178  ;

179  /*---------solve QP--------*/

180  proc optmodel printlevel=0;

181  set x_num=1..2;

181!                    * set dimension of X ;

182  set y_num=1..1;

183  set <num>DMU_ID;

184  num X{DMU_ID,x_num};

185  num Y{DMU_ID,y_num};

186  read data data_read into DMU_ID=[dmu_id]

                                            -

                                            777

NOTE 777-782: The name 'dmu_id' hides an outer declaration.

187      {r in x_num} <X[dmu_id,r]=col("x"||r)>

188      {s in y_num} <Y[dmu_id,s]=col("y"||s)>;

NOTE: There were 3 observations read from the data set WORK.DATA_READ.

189

190  var epi{DMU_ID}>=0;

191  var alpha{DMU_ID};

192  var beta{DMU_ID,x_num}>=0;

193

194  min obj= sum{q in DMU_ID} epi**2;

195  con regression{q in DMU_ID,s in y_num}:

196      Y[q,s] = alpha

197             - epi

198             + sum{r in x_num} X[q,r]*beta[q,r];

199  con concave{q in DMU_ID,h in DMU_ID}:

200         alpha + sum{r in x_num} X[q,r]*beta[q,r]

201      <= alpha + sum{r in x_num} X[q,r]*beta[h,r];

202  solve;

NOTE: Problem generation will use 4 threads.

NOTE: The constraint 'concave[1,1]' is empty.

NOTE: The constraint 'concave[2,2]' is empty.

NOTE: The constraint 'concave[3,3]' is empty.

NOTE: The problem has 12 variables (3 free, 0 fixed).

NOTE: The problem has 12 linear constraints (9 LE, 3 EQ, 0 GE, 0 range).

NOTE: The problem has 48 linear constraint coefficients.

NOTE: The problem has 0 nonlinear constraints (0 LE, 0 EQ, 0 GE, 0 range).

NOTE: The OPTMODEL presolver removed 0 variables, 3 linear constraints, and 0 nonlinear

      constraints.

NOTE: The OPTMODEL presolved problem has 12 variables, 9 linear constraints, and 0 nonlinear

      constraints.

NOTE: The QP presolver value AUTOMATIC is applied.

NOTE: The QP presolver removed 0 variables and 0 constraints.

NOTE: The QP presolver removed 0 constraint coefficients.

NOTE: The presolved problem has 12 variables, 9 constraints, and 48 constraint coefficients.

NOTE: The QP solver is called.

NOTE: The Interior Point algorithm is used.

NOTE: The deterministic parallel mode is enabled.

NOTE: The Interior Point algorithm is using up to 4 threads.

                                           Primal        Bound         Dual

      Iter   Complement  Duality Gap       Infeas       Infeas       Infeas

         0  2.91929e+03  5.84738e-01  5.84520e-01  6.60197e+01  3.94884e+04

         1  2.16097e+03  1.42333e+00  3.60634e-01  4.07325e+01  2.43634e+04

         2  1.37176e+03  5.09543e+00  7.69786e-02  8.69449e+00  5.20044e+03

         3  3.89368e+02  2.27760e+00  2.22052e-02  2.50801e+00  1.50012e+03

         4  3.92930e+02  2.51196e+00  2.18544e-02  2.46839e+00  1.47642e+03

         5  4.47907e+02  1.21485e+01  2.08696e-02  2.35716e+00  1.40989e+03

         6  2.97149e+03  1.80112e-01  1.05151e-02  1.18765e+00  7.10371e+02

         7  2.27681e+03  1.25190e-01  7.63588e-03  8.62449e-01  5.15858e+02

         8  1.16576e+03  4.90437e-02  3.61949e-03  4.08810e-01  2.44522e+02

         9  4.99641e+02  2.16038e-02  1.44582e-03  1.63301e-01  9.76752e+01

        10  4.49887e+02  3.53944e-02  1.20773e-03  1.36409e-01  8.15905e+01

        11  4.09736e+02  1.85557e-01  1.00743e-03  1.13786e-01  6.80590e+01

        12  6.36467e+03  1.65790e-01  5.39117e-04  6.08916e-02  3.64211e+01

        13  2.43454e+02  2.21331e-02  8.60910e-06  9.72371e-04  5.81605e-01

        14  2.58773e+00  2.46941e-04  8.67933e-08  9.80304e-06  5.86350e-03

        15  1.77261e-02  2.46950e-06  7.33576e-07  8.64549e-08  2.56299e-05

        16  1.77261e-04  2.46950e-08  7.33576e-09  8.64559e-10  2.56299e-07

        17  1.77269e-06  2.46962e-10  7.33592e-11  8.64698e-12  2.56296e-09

        18  1.77269e-08  2.47041e-12  7.37477e-13  1.37854e-13  2.59279e-11

NOTE: Optimal.

NOTE: Objective = 7569.

NOTE: The Interior Point solve time is 0.02 seconds.

203

204  *num epi_sol{q in DMU_ID} = epi.sol;

205  num alpha_sol{DMU_ID};

206  num beta_sol{DMU_ID,x_num};

207

208  *for{q in DMU_ID}epi_sol= epi.sol;

209  for{q in DMU_ID}alpha_sol=alpha.sol;

210  for{q in DMU_ID,r in x_num}beta_sol[q,r]=beta[q,r].sol;

211  create data epi_sol from [DMU_ID] epi;

NOTE: The data set WORK.EPI_SOL has 3 observations and 2 variables.

212  create data alpha_sol from [DMU_ID]alpha_sol;

NOTE: The data set WORK.ALPHA_SOL has 3 observations and 2 variables.

213  create data beta_sol from [DMU_ID x_num]beta_sol;

NOTE: The data set WORK.BETA_SOL has 6 observations and 3 variables.

214  quit;

NOTE: PROCEDURE OPTMODEL used (Total process time):

      real time           0.06 seconds

      cpu time            0.06 seconds

------

Thanks,

Leo.

[violet2386]

Thanks so much. I use SAS 9.2 and below is the log file. It seems that my SAS version does have some problem. However, the optimal obj calculated from matlab is zero. I hope to find what is something wrong in my code. Thanks again.

---------------------------------------------------------------------------------------------

385  data data_read;

386  input x1 x2 y1 dmu_id;

387  datalines;

NOTE: The data set WORK.DATA_READ has 3 observations and 4 variables.

NOTE: DATA statement used (Total process time):

      real time           0.03 seconds

      cpu time            0.01 seconds

391  ;

392  proc optmodel printlevel=0;

393  set x_num=1..2;

393!                 * set dimension of X ;

394  set y_num=1..1;

395  set <num>DMU_ID;

396  num X{DMU_ID,x_num};

397  num Y{DMU_ID,y_num};

398  read data data_read into DMU_ID=[dmu_id]

399  {r in x_num}<X[dmu_id,r]=col("x"||r)>

400  {s in y_num}<Y[dmu_id,s]=col("y"||s)>;

NOTE: There were 3 observations read from the data set WORK.DATA_READ.

401  var epi{DMU_ID}>=0;

402  var alpha{DMU_ID};

403  var beta{DMU_ID,x_num}>=0;

404  num epi_sol{DMU_ID};

405  num alpha_sol{DMU_ID};

406  num beta_sol{DMU_ID,x_num};

407  min obj=sum{q in DMU_ID}epi**2;

408  con regression{q in DMU_ID,s in y_num}:Y[q,s]=alpha-epi+sum{r in x_num}X[q,r]*beta[q,r];

409  con concave{q in DMU_ID,h in DMU_ID}:alpha+sum{r in x_num}X[q,r]*beta[q,r]<=alpha+sum{r in x_num}X[q,r]*beta[h,r];

410  solve;

NOTE: The constraint 'concave[1,1]' is empty.

NOTE: The constraint 'concave[2,2]' is empty.

NOTE: The constraint 'concave[3,3]' is empty.

NOTE: The problem has 12 variables (3 free, 0 fixed).

NOTE: The problem has 12 linear constraints (9 LE, 3 EQ, 0 GE, 0 range).

NOTE: The problem has 48 linear constraint coefficients.

NOTE: The problem has 0 nonlinear constraints (0 LE, 0 EQ, 0 GE, 0 range).

NOTE: The OPTMODEL presolver removed 0 variables, 3 linear constraints, and 0 nonlinear constraints.

NOTE: The OPTMODEL presolved problem has 12 variables, 9 linear constraints, and 0 nonlinear constraints.

NOTE: Using analytic derivatives for objective.

NOTE: Initial point was changed to be feasible to bound and linear constraints.

NOTE: The trust region method is used.

NOTE: The SAS System stopped processing this step because of errors.

NOTE: PROCEDURE OPTMODEL used (Total process time):

      real time           0.03 seconds

      cpu time            0.03 seconds

411  for{q in DMU_ID}epi_sol=epi.sol;

412  for{q in DMU_ID}alpha_sol=alpha.sol;

413  for{q in DMU_ID,r in x_num}beta_sol[q,r]=beta[q,r].sol;

414  create data epi_sol from [dmu_id]epi_sol;

415  create data alpha_sol from [dmu_id]alpha_sol;

416  create data beta_sol from [dmu_id x_num]beta_sol;

417  quit;

418  run;

[LeoLopes]

I am glad to help.

I have forwarded your model to someone who might be able to reproduce your problem.

There are a couple of things that may help further, if you are able to provide them:

1. Your Matlab code

2. The very top of the log file, where the detailed version information is.

Cheers,

Leo.

[LeoLopes]

Hi Violet,

Our folks suggested that if you can, please upgrade to at least 9.3. This problem does not occur there.

Technical Support may also be able to help: http://support.sas.com/techsup/contact/

Good luck and thanks for sharing!

Leo.

[violet2386]

Thanks. Yes, I should upgrade my SAS version.

[LeoLopes]

You're welcome!