OR Challenge again

[Ksharp]

Here is the question coming from :

https://communities.sas.com/t5/Base-SAS-Programming/Combining-rows-of-data/m-p/274668

The question contain three sub-questions. the last one is what I am talking about. This question is very like 

https://communities.sas.com/t5/General-SAS-Programming/Creating-Groups-of-Equal-Size/td-p/268862

@RobPratt gave the OR code, but the different thing is this question's each group have different number of members .

@RobPratt want give it a try ?

Due to the original post is too long and cumbersome. I quote here :

"

The the exact criterion for "as equally as possible," is this: we want each week to have as close to the average number of tests for each Score.  I've attached a file to show what I'm talking about.  For example, the TotalScores across all Table/Player combinations for ScoreA, ScoreB, ScoreC and ScoreD are 67, 134, 201 and 268 respectively.  The Average Scores are 17, 34, 50 and 67.  In lines 13-16 of the attached file, you see each week and the scores assigned.  Weeks 1 - 3 are pretty close to the actual averages.  Week 4 however, is lower but I think that has to do with the small data set.

Does this make sense?  All the scores need to be distributed "as equally as possible" not the total score.  "

TableList	PlayerList	ScoreA	ScoreB	ScoreC	ScoreD	Total Samples
A_C_P_AC	12	4	8	12	16	40	Week2
R_AA_AB	17	3	6	9	12	30	Week2
B_F_G_K_L_O	3,4,11	18	36	54	72	180	Week1
S_T_U_V_AD	5,6	10	20	30	40	100	Week2
D_E_H_I_J_M_N	1,2,14	21	42	63	84	210	Week3
Y,Z	13,16	4	8	12	16	40	Week4
W,X	7,15	4	8	12	16	40	Week4
Q	8,9,10	3	6	9	12	30	Week4
Total Score		67	134	201	268	670
Average Score		17	34	50	67	168
	Week1	18	36	54	72
	Week2	17	34	51	68
	Week3	21	42	63	84
	Week4	11	22	33	44

Here is my IML code:

data have;
infile cards expandtabs truncover;
input TableList : $20. PlayerList  : $20. ScoreA	ScoreB	ScoreC	ScoreD;
cards;
A_C_P_AC	12	4	8	12	16
R_AA_AB	17	3	6	9	12
B_F_G_K_L_O	3,4,11	18	36	54	72
S_T_U_V_AD	5,6	10	20	30	40
D_E_H_I_J_M_N	1,2,14	21	42	63	84
Y,Z	13,16	4	8	12	16
W,X	7,15	4	8	12	16
Q	8,9,10	3	6	9	12
;
run;



proc iml;
use have;
read all var _num_ into age[c=vname] ;
close ;

start function(x) global(age,group,nrow,ncol);
sum_group=j(group,ncol,0);
do i=1 to group;
 do j=1 to nrow;
  if x[j]=i then sum_group[i,]=sum_group[i,]+age[j,];
 end;
end;
obj=sum(sum_group[<>,]-sum_group[><,]);
return (obj);
finish;

ncol=ncol(age);
nrow=nrow(age);
group=4;  /* <--Change it(divide into 4 groups)*/

encoding=j(2,nrow,1);
encoding[2,]=group;    

id=gasetup(2,nrow,123456789);
call gasetobj(id,0,"function");
call gasetsel(id,100,1,1);
call gainit(id,1000,encoding);


niter = 10000;
do i = 1 to niter;
 call garegen(id);
 call gagetval(value, id);
end;
call gagetmem(mem, value, id, 1);

groups=t(mem);
create group var {groups};
append;
close;
print value[l = "Min Value:"] ;
call gaend(id);
quit;
 

data want;
 merge group have;
run;
proc summary data=want nway ;
 class groups;
 var _numeric_;
 output out=sum(drop=_:) sum=;
run;
proc print noobs;run;
proc print data=want noobs;run;

[RobPratt]

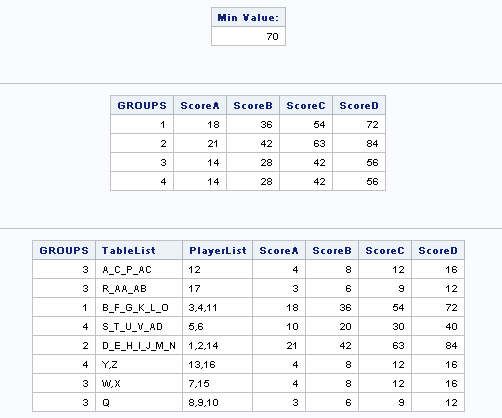
The following PROC OPTMODEL code confirms that 70 is the minimum sum of ranges:

%let num_groups = 4;
proc optmodel;
   set VARS   = {'A','B','C','D'};
   set GROUPS = 1..&num_groups;
   set OBS;
   str TableList {OBS};
   str PlayerList {OBS};
   num a {OBS, VARS};
   read data have into OBS=[_N_] TableList PlayerList {j in VARS} <a[_N_,j]=col('Score'||j)>;

   /* Assign[i,g] = 1 if observation i assigned to group g, 0 otherwise */
   var Assign {OBS, GROUPS} binary;

   con AssignOnce {i in OBS}:
      sum {g in GROUPS} Assign[i,g] = 1;

   impvar GroupSum {g in GROUPS, j in VARS} = sum {i in OBS} a[i,j] * Assign[i,g];

   var MinSum {VARS}, MaxSum {VARS};
   con MinSumCon {g in GROUPS, j in VARS}:
      MinSum[j] <= GroupSum[g,j];
   con MaxSumCon {g in GROUPS, j in VARS}:
      MaxSum[j] >= GroupSum[g,j];
   impvar Range {j in VARS} = MaxSum[j] - MinSum[j];
   min Objective = sum {j in VARS} Range[j];

   solve;

   print Assign;
   print GroupSum;
   num groupID {OBS};
   for {i in OBS} do;
      for {g in GROUPS: Assign[i,g].sol > 0.5} do;
         groupID[i] = g;
         leave;
      end;
   end;
   create data want(drop=i) from [i] TableList PlayerList {j in VARS} <col('Score'||j)=a[i,j]> groupID;
quit;

SAS Output

Assign
	1	2	3	4
1	1	0	0	0
2	1	0	0	0
3	0	0	0	1
4	0	0	1	0
5	0	1	0	0
6	0	0	1	0
7	1	0	0	0
8	1	0	0	0

GroupSum
	A	B	C	D
1	14	28	42	56
2	21	42	63	84
3	14	28	42	56
4	18	36	54	72

[Ksharp]

@RobPratt , OP have over five thousands obs/record . OR can solve that ? How many time it would be ?

[RobPratt]

The small instance solved instantly, but the performance on a larger instance is difficult to predict.  If you point me to the data, I'll give it a try.