- RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
- Mark as New
- Bookmark
- Subscribe
- Mute
- RSS Feed
- Permalink
- Report Inappropriate Content
Here is the question coming from :
https://communities.sas.com/t5/Base-SAS-Programming/Combining-rows-of-data/m-p/274668
The question contain three sub-questions. the last one is what I am talking about. This question is very like
https://communities.sas.com/t5/General-SAS-Programming/Creating-Groups-of-Equal-Size/td-p/268862
@RobPratt gave the OR code, but the different thing is this question's each group have different number of members .
@RobPratt want give it a try ?
Due to the original post is too long and cumbersome. I quote here :
"
The the exact criterion for "as equally as possible," is this: we want each week to have as close to the average number of tests for each Score. I've attached a file to show what I'm talking about. For example, the TotalScores across all Table/Player combinations for ScoreA, ScoreB, ScoreC and ScoreD are 67, 134, 201 and 268 respectively. The Average Scores are 17, 34, 50 and 67. In lines 13-16 of the attached file, you see each week and the scores assigned. Weeks 1 - 3 are pretty close to the actual averages. Week 4 however, is lower but I think that has to do with the small data set.
Does this make sense? All the scores need to be distributed "as equally as possible" not the total score. "
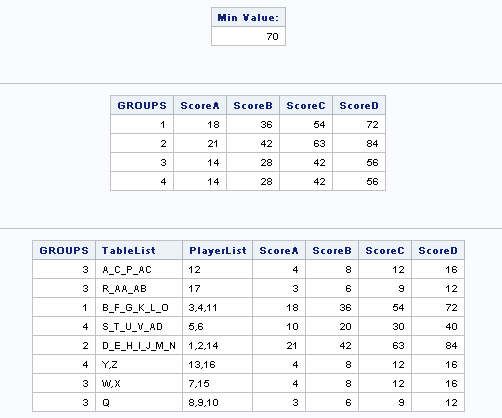
| TableList | PlayerList | ScoreA | ScoreB | ScoreC | ScoreD | Total Samples | |
| A_C_P_AC | 12 | 4 | 8 | 12 | 16 | 40 | Week2 |
| R_AA_AB | 17 | 3 | 6 | 9 | 12 | 30 | Week2 |
| B_F_G_K_L_O | 3,4,11 | 18 | 36 | 54 | 72 | 180 | Week1 |
| S_T_U_V_AD | 5,6 | 10 | 20 | 30 | 40 | 100 | Week2 |
| D_E_H_I_J_M_N | 1,2,14 | 21 | 42 | 63 | 84 | 210 | Week3 |
| Y,Z | 13,16 | 4 | 8 | 12 | 16 | 40 | Week4 |
| W,X | 7,15 | 4 | 8 | 12 | 16 | 40 | Week4 |
| Q | 8,9,10 | 3 | 6 | 9 | 12 | 30 | Week4 |
| Total Score | 67 | 134 | 201 | 268 | 670 | ||
| Average Score | 17 | 34 | 50 | 67 | 168 | ||
| Week1 | 18 | 36 | 54 | 72 | |||
| Week2 | 17 | 34 | 51 | 68 | |||
| Week3 | 21 | 42 | 63 | 84 | |||
| Week4 | 11 | 22 | 33 | 44 |
Here is my IML code:
data have;
infile cards expandtabs truncover;
input TableList : $20. PlayerList : $20. ScoreA ScoreB ScoreC ScoreD;
cards;
A_C_P_AC 12 4 8 12 16
R_AA_AB 17 3 6 9 12
B_F_G_K_L_O 3,4,11 18 36 54 72
S_T_U_V_AD 5,6 10 20 30 40
D_E_H_I_J_M_N 1,2,14 21 42 63 84
Y,Z 13,16 4 8 12 16
W,X 7,15 4 8 12 16
Q 8,9,10 3 6 9 12
;
run;
proc iml;
use have;
read all var _num_ into age[c=vname] ;
close ;
start function(x) global(age,group,nrow,ncol);
sum_group=j(group,ncol,0);
do i=1 to group;
do j=1 to nrow;
if x[j]=i then sum_group[i,]=sum_group[i,]+age[j,];
end;
end;
obj=sum(sum_group[<>,]-sum_group[><,]);
return (obj);
finish;
ncol=ncol(age);
nrow=nrow(age);
group=4; /* <--Change it(divide into 4 groups)*/
encoding=j(2,nrow,1);
encoding[2,]=group;
id=gasetup(2,nrow,123456789);
call gasetobj(id,0,"function");
call gasetsel(id,100,1,1);
call gainit(id,1000,encoding);
niter = 10000;
do i = 1 to niter;
call garegen(id);
call gagetval(value, id);
end;
call gagetmem(mem, value, id, 1);
groups=t(mem);
create group var {groups};
append;
close;
print value[l = "Min Value:"] ;
call gaend(id);
quit;
data want;
merge group have;
run;
proc summary data=want nway ;
class groups;
var _numeric_;
output out=sum(drop=_:) sum=;
run;
proc print noobs;run;
proc print data=want noobs;run;
- Mark as New
- Bookmark
- Subscribe
- Mute
- RSS Feed
- Permalink
- Report Inappropriate Content
The following PROC OPTMODEL code confirms that 70 is the minimum sum of ranges:
%let num_groups = 4;
proc optmodel;
set VARS = {'A','B','C','D'};
set GROUPS = 1..&num_groups;
set OBS;
str TableList {OBS};
str PlayerList {OBS};
num a {OBS, VARS};
read data have into OBS=[_N_] TableList PlayerList {j in VARS} <a[_N_,j]=col('Score'||j)>;
/* Assign[i,g] = 1 if observation i assigned to group g, 0 otherwise */
var Assign {OBS, GROUPS} binary;
con AssignOnce {i in OBS}:
sum {g in GROUPS} Assign[i,g] = 1;
impvar GroupSum {g in GROUPS, j in VARS} = sum {i in OBS} a[i,j] * Assign[i,g];
var MinSum {VARS}, MaxSum {VARS};
con MinSumCon {g in GROUPS, j in VARS}:
MinSum[j] <= GroupSum[g,j];
con MaxSumCon {g in GROUPS, j in VARS}:
MaxSum[j] >= GroupSum[g,j];
impvar Range {j in VARS} = MaxSum[j] - MinSum[j];
min Objective = sum {j in VARS} Range[j];
solve;
print Assign;
print GroupSum;
num groupID {OBS};
for {i in OBS} do;
for {g in GROUPS: Assign[i,g].sol > 0.5} do;
groupID[i] = g;
leave;
end;
end;
create data want(drop=i) from [i] TableList PlayerList {j in VARS} <col('Score'||j)=a[i,j]> groupID;
quit;
SAS Output
- Mark as New
- Bookmark
- Subscribe
- Mute
- RSS Feed
- Permalink
- Report Inappropriate Content
- Mark as New
- Bookmark
- Subscribe
- Mute
- RSS Feed
- Permalink
- Report Inappropriate Content
The small instance solved instantly, but the performance on a larger instance is difficult to predict. If you point me to the data, I'll give it a try.
April 27 – 30 | Gaylord Texan | Grapevine, Texas
Registration is open
Walk in ready to learn. Walk out ready to deliver. This is the data and AI conference you can't afford to miss.
Register now and save with the early bird rate—just $795!
- Discovery-based Investigation in SAS Visual Investigator – Your Guide to Better Searches | 20-Jan-2026
- SAS Bowl LVIII, SAS Viya Copilot | 21-Jan-2026
- Ask the Expert: Wie der SAS Visual Analytics Copilot Ihre Arbeit beschleunigt! | 22-Jan-2026
- Ask the Expert: The AI Advantage: How SAS Customer Intelligence 360 Solves Real Marketing Challenges | 27-Jan-2026
- DCSUG presents SAS OnDemand for Academics: the Easy Way to Learn SAS For Free for Students, Educator | 27-Jan-2026
- Ask the Expert: How to Supercharge Enterprise Agentic Workflows With SAS Retrieval Agent Manager | 05-Feb-2026
- Ask the Expert: Implementing a Digital Twin for the Monopoly Board Game Using SAS® Viya® | 12-Feb-2026