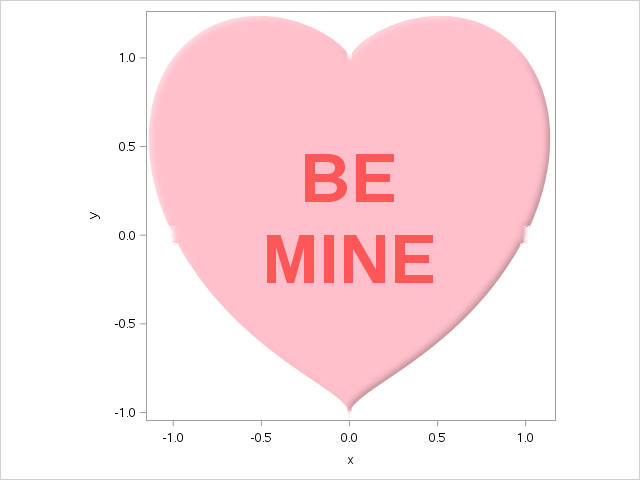
A Belated Happy (x**2+y**2-1)**3-x**2*y**3=0 Day!

[tc]

* Generate x,y pairs to closely fit Valentine equation: (x**2+y**2-1)**3-x**2*y**3=0;

data pts;
do x=-2 to 2 by .001;
  do y=-2 to 2 by .001;
    delta=abs((x**2+y**2-1)**3-x**2*y**3);
    if delta<=.00015 then do;                   * Keep closest matches; 
     a=atan2(y,x);
     output;
     end;
   end;
 end;

* Sort in angle order for polygon plot;
 
 proc sort data=pts out=pts1;
 by a delta x;
 
 data pts2;
 set pts1;
 by a;
 if first.a;                                   * Keep closest match;
 id="BE*MINE";                                 * Message for heart;
 
proc sort data=pts2; 
by a;

* Plot polygon (not quite right, but flaws look like chipped candy!);
 
proc sgplot data=pts2 aspect=1;
polygon id=id x=x y=y / fill fillattrs=(color=pink) dataskin=matte splitchar='*' 
        label=id labelattrs=(size=50pt COLOR=lightred weight=bold);
run;

[LauraRK]

this is great!!  I will file it away!

[tc]

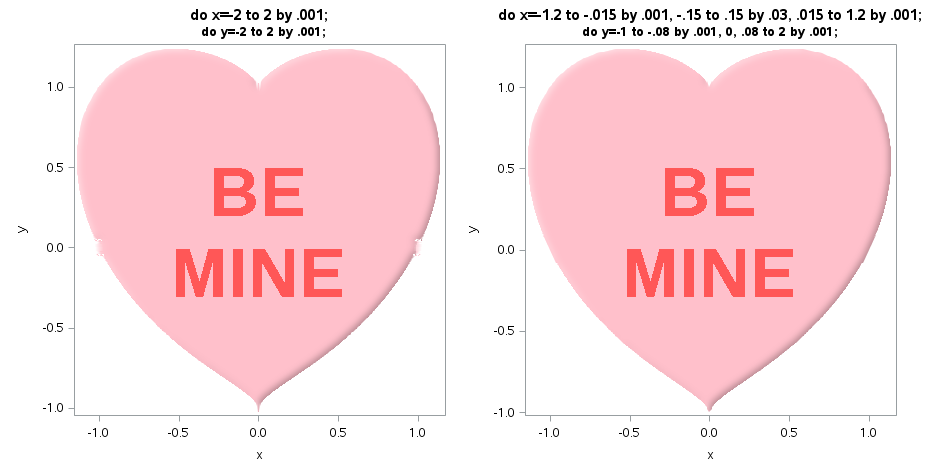
In response to my cry for help on SAS-L, Rick Wicklin suggested that if I didn't want to delve into the world of algebraic geometry just yet, I could probably obtain a better plot simply by finagling around the problematic x=0 and y=0 points, which indeed did the trick (thanks, Rick!).

Before and after images, together with the two lines of code that were tweaked to address the "crumbling" at the top and sides of the "before" Valentine: