- Home
- /
- Analytics
- /
- Stat Procs
- /
- Re: qqplot or pp plot
- RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
- Mark as New
- Bookmark
- Subscribe
- Mute
- RSS Feed
- Permalink
- Report Inappropriate Content
Hi,
I am trying qqplot/ppplot for inverse gaussian. SAS support website says to use :
proc univariate data=name;
qqplot var/ igauss(mu= lambda= );
run;
But I am getting an error. Any idea why is it not working? I can make it work for gamma but not inv gaussian. I can't find any alternatives either.
Thanks for any help.
- Mark as New
- Bookmark
- Subscribe
- Mute
- RSS Feed
- Permalink
- Report Inappropriate Content
For SAS 9.3 inverse gaussian isn't a valid parameter, the distributions options are:
Can you point to where the SAS support website provides that option?
Base SAS(R) 9.3 Procedures Guide: Statistical Procedures
Option | Description |
|---|---|
specifies beta Q-Q plot for shape parameters | |
specifies exponential Q-Q plot | |
specifies gamma Q-Q plot for shape parameter | |
specifies gumbel Q-Q plot | |
specifies lognormal Q-Q plot for shape parameter | |
specifies normal Q-Q plot | |
specifies generalized Pareto Q-Q plot for shape parameter | |
specifies power function Q-Q plot for shape parameter | |
specifies Rayleigh Q-Q plot | |
specifies three-parameter Weibull Q-Q plot for shape parameter | |
specifies two-parameter Weibull Q-Q plot |
- Mark as New
- Bookmark
- Subscribe
- Mute
- RSS Feed
- Permalink
- Report Inappropriate Content
here is for ppplot:
Base SAS(R) 9.3 Procedures Guide: Statistical Procedures
got the igauss syntex from here:
Base SAS(R) 9.3 Procedures Guide: Statistical Procedures
Is there any way to get qqplot for inverse gaussian if proc univariate does not work.
Thanks
- Mark as New
- Bookmark
- Subscribe
- Mute
- RSS Feed
- Permalink
- Report Inappropriate Content
In 9.3, you can get a ppplot, but not a qqplot. If you check the documentation, igauss is only a valid option on ppplot. I just did this using:
proc univariate data=a;
var x;
ppplot x / igauss;
run;
- Mark as New
- Bookmark
- Subscribe
- Mute
- RSS Feed
- Permalink
- Report Inappropriate Content
Hmmm! it is pretty strange. If I try the exact code with gamma option, it works, but iguass option does not work. SAS does not even recognize it as a valid option.
Thanks for the help.
- Mark as New
- Bookmark
- Subscribe
- Mute
- RSS Feed
- Permalink
- Report Inappropriate Content
Its not a valid option for qqplot according to the SAS Docs.
The only way I could think of is pretty much brute force, generating the values and using proc gplot.
- Mark as New
- Bookmark
- Subscribe
- Mute
- RSS Feed
- Permalink
- Report Inappropriate Content
Since the inverse Gaussian is an exponential family, you might try:
proc univariate data=a;
var x;
qqplot x / exponential;
run;
A reference line can be inserted by noting that THETA=-lambda/(2*mu*mu) and SIGMA=-lambda/2 (I think. Those might be reversed). And no guarantees on this one--it's just a possibility.
Steve Denham
- Mark as New
- Bookmark
- Subscribe
- Mute
- RSS Feed
- Permalink
- Report Inappropriate Content
Steve,
Your code does work. However, I need to draw a reference line at 45 degree for comparison. It might be a silly question, but I could not find any resources for help with that. Thanks!
- Mark as New
- Bookmark
- Subscribe
- Mute
- RSS Feed
- Permalink
- Report Inappropriate Content
Today's scary approach:
proc univariate data=a;
var x;
qqplot x / exponential(theta=est sigma=est);
run;
That should give you a 45 degree line, and estimates of theta and sigma. From those values, you can calculate lambda and mu for the inverse gaussian.
Why is this scary? It's untested, and right now, I don't have time to write a program that would generate 1000 inv-gaussian random variates with known lambda and mu values to check it.
Steve Denham
- Mark as New
- Bookmark
- Subscribe
- Mute
- RSS Feed
- Permalink
- Report Inappropriate Content
You can produce the quantiles for IGAUSS and use them to produce a Q-Q plot. See Modeling the distribution of data? Create a Q-Q plot - The DO Loop
You can use the LINEPARM statement in PROC SGPLOT to produce a diagonal line. See Add a diagonal line to a scatter plot: The SAS 9.3 way - The DO Loop
- Mark as New
- Bookmark
- Subscribe
- Mute
- RSS Feed
- Permalink
- Report Inappropriate Content
Hi Rick,
Thanks for your reply. There are many useful information on the links you provided. I was able to get the qqplot as per your instruction. However, I was not able to draw the diagonal line because I am using SAS9.2 so lineparm will not work.
Thanks much,
-CD
- Mark as New
- Bookmark
- Subscribe
- Mute
- RSS Feed
- Permalink
- Report Inappropriate Content
The very first sentence of the blog post "Add a diagonal line..." contains a link to an article that shows how to add a diagonal line at SAS 9.2.
April 27 – 30 | Gaylord Texan | Grapevine, Texas
Registration is open
Walk in ready to learn. Walk out ready to deliver. This is the data and AI conference you can't afford to miss.
Register now and lock in 2025 pricing—just $495!
ANOVA, or Analysis Of Variance, is used to compare the averages or means of two or more populations to better understand how they differ. Watch this tutorial for more.
Find more tutorials on the SAS Users YouTube channel.
 and
and 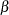 specified with mandatory ALPHA= and BETA= beta-options
specified with mandatory ALPHA= and BETA= beta-options  specified with mandatory SIGMA= lognormal-option
specified with mandatory SIGMA= lognormal-option  specified with mandatory C= Weibull-option
specified with mandatory C= Weibull-option 


