- Home
- /
- Analytics
- /
- Stat Procs
- /
- non-parametrical 2 way Anova/mixed model with multiple comparisons
- RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
- Mark as New
- Bookmark
- Subscribe
- Mute
- RSS Feed
- Permalink
- Report Inappropriate Content
Dear Community,
Do you know of any option to do a non-parametric kind of 2way Anova/mixed model analysis with the option for multiple comparisons and an adequate adjustment?
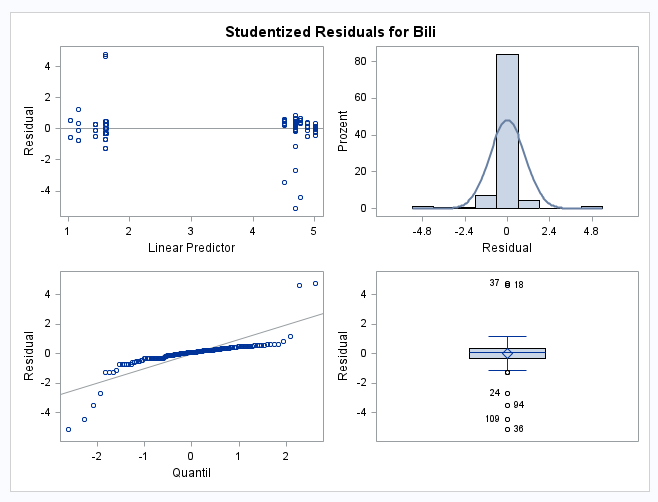
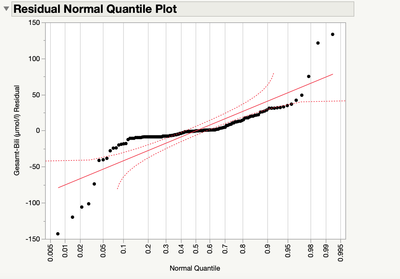
I have data of a rather dichotomous character which can’t be transformed into a Gaussian distribution and would therefore violate the assumptions of a regular ANOVA/mixed model analysis. I have measured Bilirubin at 5 Endpoints (28d, 31d, 35d, 42d and 56d) on two treatment levels (control, treatment). Its not a repeated measurements design but different subjects at each endpoint respectively. You will find a quick plot of the data attached to get a better understanding how the data are structured, as well as a QQ Plot and the studentized residuals.
Thank you very much!
best Moritz
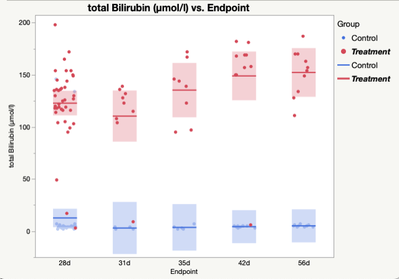
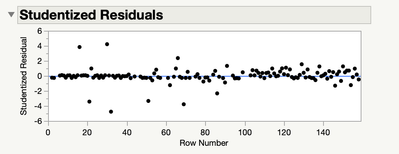
- Mark as New
- Bookmark
- Subscribe
- Mute
- RSS Feed
- Permalink
- Report Inappropriate Content
I have data of a rather dichotomous character which can’t be transformed into a Gaussian distribution and would therefore violate the assumptions of a regular ANOVA/mixed model analysis.
I assume these dichotomous character variables are predictor variables. ANOVA does not require predictor variables to have a Gaussian distribution. No transformation is needed. Everything you are trying to do can be done in ANOVA without violating assumptions.
proc glm data=have;
class endpoint treatment;
model billirubin = endpoint treatment;
run;
quit;Paige Miller
- Mark as New
- Bookmark
- Subscribe
- Mute
- RSS Feed
- Permalink
- Report Inappropriate Content
Dear Paige,
thank you very much for your reply!
Bilirubin was measured in blood-samples at the respective endpoints and should be a continuous response variable and not a predictor variable, it just shows a rather dichotomous distribution, because the values are either very high in response to the treatment or very low in the control group. And the distribution of the residuals of the response variable must be specified, doesn't it?
Maybe my explanation above was not specific enough or I misunderstood something.
I measured some other values, for instance cytokines that showed a logN distribution as expected. Those were analyzed using PROC GLIMMIX as shown below. I am looking for an alternativ if the distribution is unknown.
best Moritz
proc glimmix data=my_data; Class group Endpoint; Model measured_value = Group Endpoint Group*Endpoint /dist=logN ddfm=kr2; Random _resid_ /group=Group; covtest homogeneity; output out=resids resid=r; LSMeans Group*Endpoint/ slicediff=Endpoint adjust=sim stepdown(type=logical) adjdfe=row lines plot=meanplot(sliceby=group join cl); run; Proc univariate data=resids normaltest; var r; qqplot; run;
- Mark as New
- Bookmark
- Subscribe
- Mute
- RSS Feed
- Permalink
- Report Inappropriate Content
Response variables do not have to have a Gaussian distribution either. The errors have to be Gaussian. You will notice that in the code I provided above, billirubin was the response variable.
The fact that the values of Y vary greatly based upon treatment or control group can be accounted for in the model by including treatment into the model.
Paige Miller
- Mark as New
- Bookmark
- Subscribe
- Mute
- RSS Feed
- Permalink
- Report Inappropriate Content
Hey Paige, thanks again for helping me to sort this out.
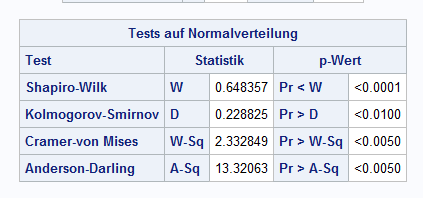
As stated in the article you need to check the residuals for approximate normality. And that is what I did. Please forgive me the sloppy simplification to state that my data are not gaussian. But to demonstrate the non-normality of the residuals I provided a residual normal quantile plot. To my mind it looks like a systematic deviation and not a random scatter, you will find the tests for normality of the residuals attached.
Of course treatment was included into the model in terms of the group variable (the groups are 'control' and 'treatment').
best Moritz
- Mark as New
- Bookmark
- Subscribe
- Mute
- RSS Feed
- Permalink
- Report Inappropriate Content
That's good, we now see that the residuals are not normally distributed. Once again, @Rick_SAS has the explanation: https://blogs.sas.com/content/iml/2022/08/17/box-cox-regression.html
Paige Miller
- Mark as New
- Bookmark
- Subscribe
- Mute
- RSS Feed
- Permalink
- Report Inappropriate Content
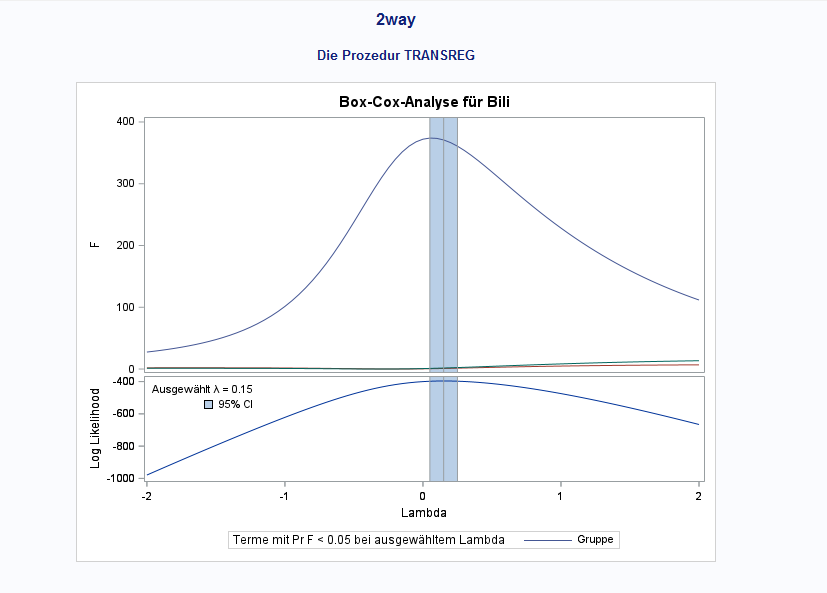
Its not that I haven't tried box-cox yet, but I like the concept of using box-cox to get an idea of the next best distribution. After using the suggested code as displayed:
proc sql noprint;
select 1-min(bili) into :c trimmed from my_data;
quit;
%put &=c;
proc transreg data=my_data ss2 details plots=(boxcox);
model BoxCox(bili / parameter=&c geometricmean
convenient lambda=-2 to 2 by 0.05) = identity( group | Endpoint);
output out=TransOut residual;
run;
proc univariate data=TransOut(keep=Rbili);
histogram Rbili / normal kernel;
qqplot Rbili / normal(mu=est sigma=est) grid;
ods select histogram qqplot GoodnessOfFit Moments;
run;I got the following results which still do not look 'normal enough' do they?
Just to get this right, if the box-cox CONVIENIENT option would have suggested for instance a Lamda=0 and the residuals would have been approximately normal, lets say everything p>0.01, I could have used the parametric approach with dist=logN?
- Mark as New
- Bookmark
- Subscribe
- Mute
- RSS Feed
- Permalink
- Report Inappropriate Content
It may be that there are no obvious transformations that turn your data into something that has close to normal errors.
Paige Miller
- Mark as New
- Bookmark
- Subscribe
- Mute
- RSS Feed
- Permalink
- Report Inappropriate Content
@PaigeMiller wrote:
It may be that there are no obvious transformations that turn your data into something that has close to normal errors.
Seems that a sentence of mine never made it ... I want to add that if you can determine what distribution is a better fit than the normal distribution, you can use PROC GLIMMIX (if that distribution is available in PROC GLIMMIX).
Paige Miller
- Mark as New
- Bookmark
- Subscribe
- Mute
- RSS Feed
- Permalink
- Report Inappropriate Content
And if there is no transformation to turn my data into something with close to normal errors, aren’t we eventually back at my initial question if there is any non-parametric alternative?
- Mark as New
- Bookmark
- Subscribe
- Mute
- RSS Feed
- Permalink
- Report Inappropriate Content
I added the sentence ... in my previous reply.
So here is some code for non-parametric two-way ANOVA.
https://support.sas.com/documentation/onlinedoc/stat/ex_code/121/friedman.html
Paige Miller
- Mark as New
- Bookmark
- Subscribe
- Mute
- RSS Feed
- Permalink
- Report Inappropriate Content
- Mark as New
- Bookmark
- Subscribe
- Mute
- RSS Feed
- Permalink
- Report Inappropriate Content
Maybe you could make a new variable like:
new=catx('|',sex,age);
And using one way non-parameter
proc npar1way wilcoxon ;
class new;
var .....
run;
- Mark as New
- Bookmark
- Subscribe
- Mute
- RSS Feed
- Permalink
- Report Inappropriate Content
Thanks for helping me! Already thought about that, but hoped that there is a more elegant way.
Best Moritz
April 27 – 30 | Gaylord Texan | Grapevine, Texas
Registration is open
Walk in ready to learn. Walk out ready to deliver. This is the data and AI conference you can't afford to miss.
Register now and lock in 2025 pricing—just $495!
ANOVA, or Analysis Of Variance, is used to compare the averages or means of two or more populations to better understand how they differ. Watch this tutorial for more.
Find more tutorials on the SAS Users YouTube channel.