- Home
- /
- Analytics
- /
- Stat Procs
- /
- Re: Why no strata-statement in PROC GLM?
- RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
- Mark as New
- Bookmark
- Subscribe
- Mute
- RSS Feed
- Permalink
- Report Inappropriate Content
I wonder why there is no strata statement in PROC GLM, or PROC REG. Others has sometimes suggested it on this forum. Now I try explain how I imagine it should work.
Lets say we have an outcome "y", a class variable "Group" and two other covariates "A" and "B". We are not interested in the group effect, only we want the estimate for A and B. Easily, the estimates can be calculated with PROC GLM:
proc glm data =mydata;
class group;
model y=group A B/solution;
run;
quit;However, in case there are a huge number of levels in the "Group"-variable the estimation can take long and require lots of resources.
Instead, the estimates can be calculated in the orthogonal space to the collumns vectors created by the Group-variable. Doing this will give exactly same estimates. That is, the outcome vector as well as the collumns vectors for the covariates of interest should be projected into the orthogonal space from the covariates of nointerest. The estimates can now be calculated by using the projected outcomevector as outcome and the projected covariate vectors as covariates.
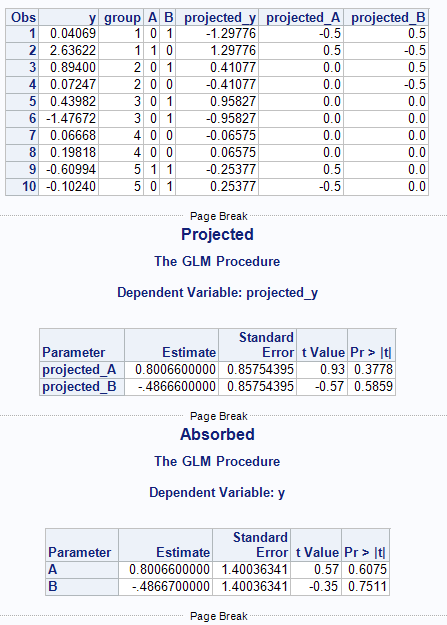
A simple example with just 5 levels in the group-variable.
| y | group | A | B | projected_y | projected_A | projected_B |
|---|---|---|---|---|---|---|
| 0.04069 | 1 | 0 | 1 | -1.29776 | -0.5 | 0.5 |
| 2.63622 | 1 | 1 | 0 | 1.29776 | 0.5 | -0.5 |
| 0.89400 | 2 | 0 | 1 | 0.41077 | 0.0 | 0.5 |
| 0.07247 | 2 | 0 | 0 | -0.41077 | 0.0 | -0.5 |
| 0.43982 | 3 | 0 | 1 | 0.95827 | 0.0 | 0.0 |
| -1.47672 | 3 | 0 | 1 | -0.95827 | 0.0 | 0.0 |
| 0.06668 | 4 | 0 | 0 | -0.06575 | 0.0 | 0.0 |
| 0.19818 | 4 | 0 | 0 | 0.06575 | 0.0 | 0.0 |
| -0.60994 | 5 | 1 | 1 | -0.25377 | 0.5 | 0.0 |
| -0.10240 | 5 | 0 | 1 | 0.25377 | -0.5 | 0.0 |
proc glm data =mydata;
model projected_y=projected_A projected_B/solution noint;
run;
quit;
So, what I suggest is that the STRATA-statement should tell PROC GLM to projecting the outcome and covariates into the orthogonal space to the collumn space of variable(s) in the STRATA statement.
One will maybe notice that the projection matrix which is needed can be quite large, and may therefore also be cumbersome to calculate. But, in cases where it is only a single class variable that should be "stratified out" the projection matrix can be calculate in a quite simple way without using the slow (O(N^3)) algorithm for calculating matrix inverses.
Im happy to hear any comments on this idea.
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- RSS Feed
- Permalink
- Report Inappropriate Content
Maybe ABSORB is what you're looking for.
data y;
infile cards expandtabs;
input y group A B projected_y projected_A projected_B;
cards;
0.04069 1 0 1 -1.29776 -0.5 0.5
2.63622 1 1 0 1.29776 0.5 -0.5
0.89400 2 0 1 0.41077 0.0 0.5
0.07247 2 0 0 -0.41077 0.0 -0.5
0.43982 3 0 1 0.95827 0.0 0.0
-1.47672 3 0 1 -0.95827 0.0 0.0
0.06668 4 0 0 -0.06575 0.0 0.0
0.19818 4 0 0 0.06575 0.0 0.0
-0.60994 5 1 1 -0.25377 0.5 0.0
-0.10240 5 0 1 0.25377 -0.5 0.0
;;;;
run;
proc print;
run;
title 'Projected';
ods select ParameterEstimates;
proc glm data=y;
model projected_y=projected_A projected_B/solution noint;
run;
quit;
title 'Absorbed';
ods select ParameterEstimates;
proc glm data=y;
absorb group;
model y = a b / solution noint;
run;
- Mark as New
- Bookmark
- Subscribe
- Mute
- RSS Feed
- Permalink
- Report Inappropriate Content
Maybe ABSORB is what you're looking for.
data y;
infile cards expandtabs;
input y group A B projected_y projected_A projected_B;
cards;
0.04069 1 0 1 -1.29776 -0.5 0.5
2.63622 1 1 0 1.29776 0.5 -0.5
0.89400 2 0 1 0.41077 0.0 0.5
0.07247 2 0 0 -0.41077 0.0 -0.5
0.43982 3 0 1 0.95827 0.0 0.0
-1.47672 3 0 1 -0.95827 0.0 0.0
0.06668 4 0 0 -0.06575 0.0 0.0
0.19818 4 0 0 0.06575 0.0 0.0
-0.60994 5 1 1 -0.25377 0.5 0.0
-0.10240 5 0 1 0.25377 -0.5 0.0
;;;;
run;
proc print;
run;
title 'Projected';
ods select ParameterEstimates;
proc glm data=y;
model projected_y=projected_A projected_B/solution noint;
run;
quit;
title 'Absorbed';
ods select ParameterEstimates;
proc glm data=y;
absorb group;
model y = a b / solution noint;
run;
- Mark as New
- Bookmark
- Subscribe
- Mute
- RSS Feed
- Permalink
- Report Inappropriate Content
This topic is outside of my area of expertise, so I should probably not comment. However, you asked for "any comments," so I hope you'll excuse me if I am misreading your message.
In my limited understanding of "stratified regression," observations are selected through probability sampling, which means that there is an "inverse probability" weight associated with each observation. A consequence is that the usual OLS assumptions are not satisfied. In particular, E(Y | X=x) is not equal to x*beta_LS (where beta_LS are the usual OLS estimates) and the distribution of errors (conditioned on X) is not normal. The SURVEYREG procedure has an example of stratified regression.
So to me, the analysis that you've described is not stratified regression. That said, if you want to carry out the analysis that you've outlined, I think you can do that in SAS. Your description sounds like a partial regression analysis that can be carried out by calling a regression procedure three times:
1) MODEL Y = group; and output Y_Proj = residuals of this model.
2) MODEL A B = group; and output A_Proj and B_Proj, which are the residuals
3) MODEL Y_Proj = A_Proj B_Proj;
- Mark as New
- Bookmark
- Subscribe
- Mute
- RSS Feed
- Permalink
- Report Inappropriate Content
Jacob,
My two cents. STRAT statement(condition regression) is only for MLE ,not for OLS(uncondition regression) . That is reason why proc genmod have STRATA .
- Mark as New
- Bookmark
- Subscribe
- Mute
- RSS Feed
- Permalink
- Report Inappropriate Content
Thank you for your comments. I see that it is already implemented, it is just called "absorb" instead of STRATA. I must confess that I had not noticed this before now.
@Ksharp: I disagree a bit with you. Although I came to the estimating for parameters of interest estimations by using projections on the estimation equations from OLS, the same estimation equations can be obtained by conditioning on the sum of the outcome variables within each level of the variable in the ABSORB statement. Thereby, using the ABSORB statement can be viewed as a conditional regression.
@Rick_SAS: I think I was not clear enugh what I meant with "STRATA". Unfortunately "strata" have many different meanings. What I meant was to "stratify" the baseline level. This is same meaning as how "STRATA" is to be understood in proc phreg or proc logistic, and therefore I expected it also to be termed as "STRATA" in proc glm. Strata in surveysampling is a quite different topic.
ANOVA, or Analysis Of Variance, is used to compare the averages or means of two or more populations to better understand how they differ. Watch this tutorial for more.
Find more tutorials on the SAS Users YouTube channel.