- Home
- /
- Analytics
- /
- Stat Procs
- /
- Welch's ANOVA With Geometric Means
- RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
- Mark as New
- Bookmark
- Subscribe
- Mute
- RSS Feed
- Permalink
- Report Inappropriate Content
I am not super familiar with Welch's ANOVA nor geometric means, so a detailed response is appreciated.
I am interested in comparing concentrations among BMI groups (not obese, obese, severely obese) within two different time points (after start of treatment, after end of treatment). Since we are assuming unequal variances, I thought Welch's ANOVA would work well to check if at least one group is different. However, since geometric mean and geometric cv are what's being reported, I thought I should compare geometric means rather than arithmetic means.
(1) Is there a way to compare geometric means using ANOVA? I know the geometric mean is the exponentiated mean of the log-transformed data, but I am unsure how to apply that to ANOVA.
(2) Is it even necessary to use the geometric mean if I use Welch's ANOVA?
(3) Is there a simple way to store the p-value from the output table, so I can add it to a summary table later on? My plan was to use PROC SQL to add a row to the bottom of my "Data Have" with a p-value.
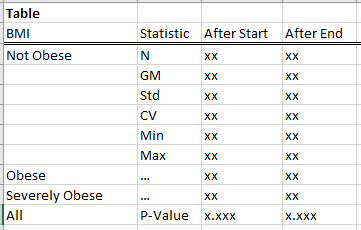
Generally, I want a table like this (will use PROC REPORT):
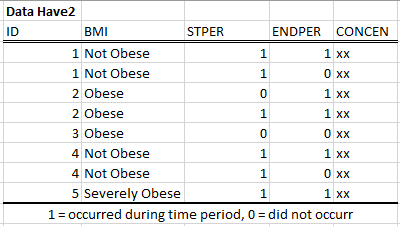
My datasets are organized like this:
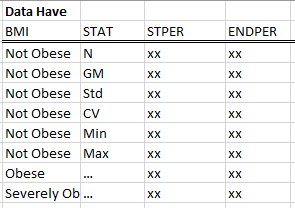
xx represents some numerical value.
Thank you in advance!
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- RSS Feed
- Permalink
- Report Inappropriate Content
Consider this code:
proc glimmix data=have;
ods output lsmeans=lsmeans;
class bmi time;
model concentration = bmi time bmi*time/dist=lognormal ddfm=satterthwaite;
random _residual_/group=bmi;
lsmeans bmi time bmi*time/cl;
run;If you have the first and second observation for each subject, you could change this to:
proc glimmix data=have;
ods output lsmeans=lsmeans;
class bmi time sub_ID;
model concentration = bmi time bmi*time/dist=lognormal ddfm=satterthwait;
random _residual_/group=bmi subject=sub_ID;
lsmeans bmi time bmi*time/cl;
run;This requires a "long" version of the data, where each line has one subject_ID, one BMI and one time. You could add in a test for homogeneity of variance, but these two blocks are closer to the assumption in a Welch's t test of unequal variances. If the variances are grossly different by group, that Satterthwaite approximation for the denominator degrees of freedom is appropriate.
So this results in a dataset that has the estimates and the 95% confidence bounds on the natural log scale. To get geometric means and bounds, simply exponentiate these values in a DATA step.
SteveDenham
- Mark as New
- Bookmark
- Subscribe
- Mute
- RSS Feed
- Permalink
- Report Inappropriate Content
Hello,
This post may be of interest to you:
ANOVA using geometric mean
https://communities.sas.com/t5/Statistical-Procedures/ANOVA-using-geometric-mean/m-p/303654#M16143
Koen
- Mark as New
- Bookmark
- Subscribe
- Mute
- RSS Feed
- Permalink
- Report Inappropriate Content
So long as all your values are greater than zero, you can log transform and do Welch's ANOVA to test if the log(means) are different. Since the backtransfomation is monotonic, you are getting p values for differences between the geometric means.
However, I would encourage you to make a leap ahead from the 1950's (when Welch presented his method) to something that uses a generalized linear model, and allows you to model the heteroscedasticity (PROC GLIMMIX using the GROUP= option in the RANDOM statement, and a lognormal distribution).
SteveDenham
- Mark as New
- Bookmark
- Subscribe
- Mute
- RSS Feed
- Permalink
- Report Inappropriate Content
Thank you.
I am not familiar with PROC GLIMMIX and will have to look into it. You mentioned to use the GROUP = option in the RANDOM statement. Would I be making my BMI groups random? I've had limited experience working with mixed effects models in school, so I'm not great at assessing what should be treated as fixed vs. random.
- Mark as New
- Bookmark
- Subscribe
- Mute
- RSS Feed
- Permalink
- Report Inappropriate Content
Consider this code:
proc glimmix data=have;
ods output lsmeans=lsmeans;
class bmi time;
model concentration = bmi time bmi*time/dist=lognormal ddfm=satterthwaite;
random _residual_/group=bmi;
lsmeans bmi time bmi*time/cl;
run;If you have the first and second observation for each subject, you could change this to:
proc glimmix data=have;
ods output lsmeans=lsmeans;
class bmi time sub_ID;
model concentration = bmi time bmi*time/dist=lognormal ddfm=satterthwait;
random _residual_/group=bmi subject=sub_ID;
lsmeans bmi time bmi*time/cl;
run;This requires a "long" version of the data, where each line has one subject_ID, one BMI and one time. You could add in a test for homogeneity of variance, but these two blocks are closer to the assumption in a Welch's t test of unequal variances. If the variances are grossly different by group, that Satterthwaite approximation for the denominator degrees of freedom is appropriate.
So this results in a dataset that has the estimates and the 95% confidence bounds on the natural log scale. To get geometric means and bounds, simply exponentiate these values in a DATA step.
SteveDenham
- Mark as New
- Bookmark
- Subscribe
- Mute
- RSS Feed
- Permalink
- Report Inappropriate Content
If I only care that at least one BMI group is different, I assume I can go off of the Type III Tests of Fixed Effects table.
How would you describe this type of test? That is, before I had the footnote on my table "BMI groups were compared using Welch's ANOVA." Since this is no longer Welch's ANOVA, what would the test be called?
- Mark as New
- Bookmark
- Subscribe
- Mute
- RSS Feed
- Permalink
- Report Inappropriate Content
ANOVA with nonhomogeneous errors.
Might need to spell out ANOVA as analysis of variance.
SteveDenham
April 27 – 30 | Gaylord Texan | Grapevine, Texas
Registration is open
Walk in ready to learn. Walk out ready to deliver. This is the data and AI conference you can't afford to miss.
Register now and save with the early bird rate—just $795!
ANOVA, or Analysis Of Variance, is used to compare the averages or means of two or more populations to better understand how they differ. Watch this tutorial for more.
Find more tutorials on the SAS Users YouTube channel.