- Home
- /
- Analytics
- /
- Stat Procs
- /
- Re: Weighted v Unweighted data in proc means and proc univariate
- RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
- Mark as New
- Bookmark
- Subscribe
- Mute
- RSS Feed
- Permalink
- Report Inappropriate Content
I have been answering along to https://communities.sas.com/t5/SAS-Procedures/weighted-percentiles/m-p/294127#U294127 the weighted percetiles article posted by Lida and it got me thinking about the differences between the weighted and unweighted statistics, so I put together a little expirement.
I would create a dataset which had the same observations but weighted and a second dataset that had them laid out as individual records to determine if there was a difference, and particularly if it could affect the percentiles (which was Lida's question in the first place). So here is what I found.
This should create two datasets LFC and LFC2 which are identical once the weights are applied.
DATA lfc;
INPUT club $ goalspergame numgames ;
DATALINES;
Liverpool 5 3
Liverpool 6 5
Liverpool 2 3
Liverpool 0 1
Liverpool 1 4
Liverpool 3 2
;
data lfc2;
INPUT club $ goalspergame;
DATALINES;
Liverpool 5
Liverpool 5
Liverpool 5
Liverpool 6
Liverpool 6
Liverpool 6
Liverpool 6
Liverpool 6
Liverpool 2
Liverpool 2
Liverpool 2
Liverpool 0
Liverpool 1
Liverpool 1
Liverpool 1
Liverpool 1
Liverpool 3
Liverpool 3
; First two the question about percentiles and if they infact can be altered by weights.
proc means data=lfc min max mean stddev q1 median q3 p10;
var goalspergame;
run;
proc means data=lfc min max mean stddev q1 median q3 p10;
var goalspergame;
weight numgames;
run;Which demonstrates that you can infact alter the percntiles with weights, as p10 in the unweighted is 0, and in the weighted it is 1.
SAS Output
| Unweighted |
| Analysis Variable : goalspergame | |||||||
|---|---|---|---|---|---|---|---|
| Minimum | Maximum | Mean | Std Dev | Lower Quartile | Median | Upper Quartile | 10th Pctl |
| 0 | 6.0000000 | 2.8333333 | 2.3166067 | 1.0000000 | 2.5000000 | 5.0000000 | 0 |
| Weighted |
| Analysis Variable : goalspergame | |||||||
|---|---|---|---|---|---|---|---|
| Minimum | Maximum | Mean | Std Dev | Lower Quartile | Median | Upper Quartile | 10th Pctl |
| 0 | 6.0000000 | 3.3888889 | 4.0565448 | 1.0000000 | 3.0000000 | 6.0000000 | 1.0000000 |
But say you didn't want to use the weighted dataset and you felt like typing out each line, ie LFC2, would you get the same results as if you used the weighted? Sort of...
proc means data=lfc min max mean stddev q1 median q3 p10;
var goalspergame;
weight numgames;
title "Weighted";
run;
proc means data=lfc2 min max mean stddev q1 median q3 p10;
var goalspergame;
title "individual rows";
run;
SAS Output
| Weighted |
| Analysis Variable : goalspergame | |||||||
|---|---|---|---|---|---|---|---|
| Minimum | Maximum | Mean | Std Dev | Lower Quartile | Median | Upper Quartile | 10th Pctl |
| 0 | 6.0000000 | 3.3888889 | 4.0565448 | 1.0000000 | 3.0000000 | 6.0000000 | 1.0000000 |
| Individual Lines |
| Analysis Variable : goalspergame | |||||||
|---|---|---|---|---|---|---|---|
| Minimum | Maximum | Mean | Std Dev | Lower Quartile | Median | Upper Quartile | 10th Pctl |
| 0 | 6.0000000 | 3.3888889 | 2.1999703 | 1.0000000 | 3.0000000 | 6.0000000 | 1.0000000 |
But if you look all of the statistics are the same except for the Std Dev, and if you look at proc univariate the variance and kurtosis are also different between the data that is weighted, and the data which is written out. So my question is why? And this is PC-SAS 9.4.
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- RSS Feed
- Permalink
- Report Inappropriate Content
You are confusing weights and frequencies. For the formulas for weighted descriptive statistics, see the doc for MEAN and StdDev. For weighted percentiles, see the doc for percentiles.
A positive integer frequency is easy to understand: all statistics will be the same as if you replicate each record 'freq[i]' number of times. A frequency variable is just a notational convenience to save you from typing duplicate records.
A weight changes statistics by giving more weight to some observations than others. I have written about the weighted mean in SAS. I have also shown that frequencies and weights give different results for regression analyses.
To compute percentiles, you order the data and create the empirical cumulative distribution (ECDF). Say your data are
1,2,3,4,5,6
In an unweighted analysis, each datum accounts for 1/n=1/6th of the sample, so the ECDF is a piecewise contant function that increases by 1/6 at each datum. To find a quantile, you start on the Y axis, move across until you hit a "vertical line", which gives you a datum value (for the default PCTL=5 method). (I am omitting details such as the median for an even number of points is the averagea of two data values). The computation follows:
/* unweighted percentiles */
data a;
input x @@;
datalines;
1 2 3 4 5
;
proc univariate data=a;
cdf x;
run;
proc means data=a p20 p40 p60 p80;
var x;
run;
In a weighted analysis, the ECDF does not increase by 1/n at each datum. Instead, the ECDF increases by w[i]/W where W=sum_i w[i] is the sum of the weights. (This is equivalent to choosing weight that sum to 1, which would represent the proportion of weight for each datum.) Thus the unweighted percentile p is not necessarily equal to the weighted percentile for p. However, the extreme values (min=0th percentile; max=100th percentile) remain unchanged because they are the endpoints of the weighted ECDF, which still increases from 0 to 1.
For example, suppose you choose weights
x: 1, 2, 3, 4, 5, 6
wt: 0.3, 0.2, 0.05, 0.1, 0.3, 0.05
Then the following computation finds the weighted percentiles:
data Wt;
input x wt;
datalines;
1 0.3
2 0.2
3 0.05
4 0.1
5 0.3
6 0.05
;
proc means data=Wt p20 p40 p60 p80;
var x;
weight wt;
run;
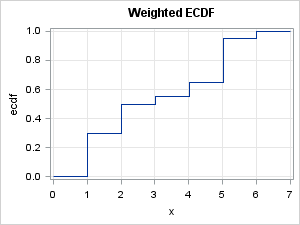
The corresponding weighted ECDF looks like this:
To find the 20th weighted pctl, start at 0.2 on the Y axis. Go over until you hit the graph, then go down to get x=1.
To find the 40th weighted pctl, start at 0.4 on the Y axis. Go over until you hit the graph, then go down to get x=2
In a similar way, the 60th weighted pctl is x=4 and the 80th weighted pctl is x=5.
- Mark as New
- Bookmark
- Subscribe
- Mute
- RSS Feed
- Permalink
- Report Inappropriate Content
I think that's stated in the documentation.
If you need standard deviation use proc surveymeans?
- Mark as New
- Bookmark
- Subscribe
- Mute
- RSS Feed
- Permalink
- Report Inappropriate Content
- Mark as New
- Bookmark
- Subscribe
- Mute
- RSS Feed
- Permalink
- Report Inappropriate Content
So, this is a question that's come up before and will again and I know there's an answer that makes sense, but can't recall right now.
I'll move this post to the Statistical Procedures Forum and see if @Rick_SAS can contribute 🙂
- Mark as New
- Bookmark
- Subscribe
- Mute
- RSS Feed
- Permalink
- Report Inappropriate Content
And since your "weight" variable is actually a count then the results of:
proc means data=lfc min max mean stddev q1 median q3 p10;
var goalspergame;
freq numgames;
run;Pretty much match exactly the results from
proc means data=lfc2 min max mean stddev q1 median q3 p10;
var goalspergame;
run;title;The NUMBER of observations is very important when looking at standard deviation. WEIGHT does not affect the N used in the calculation, FREQ does however.
- Mark as New
- Bookmark
- Subscribe
- Mute
- RSS Feed
- Permalink
- Report Inappropriate Content
You are confusing weights and frequencies. For the formulas for weighted descriptive statistics, see the doc for MEAN and StdDev. For weighted percentiles, see the doc for percentiles.
A positive integer frequency is easy to understand: all statistics will be the same as if you replicate each record 'freq[i]' number of times. A frequency variable is just a notational convenience to save you from typing duplicate records.
A weight changes statistics by giving more weight to some observations than others. I have written about the weighted mean in SAS. I have also shown that frequencies and weights give different results for regression analyses.
To compute percentiles, you order the data and create the empirical cumulative distribution (ECDF). Say your data are
1,2,3,4,5,6
In an unweighted analysis, each datum accounts for 1/n=1/6th of the sample, so the ECDF is a piecewise contant function that increases by 1/6 at each datum. To find a quantile, you start on the Y axis, move across until you hit a "vertical line", which gives you a datum value (for the default PCTL=5 method). (I am omitting details such as the median for an even number of points is the averagea of two data values). The computation follows:
/* unweighted percentiles */
data a;
input x @@;
datalines;
1 2 3 4 5
;
proc univariate data=a;
cdf x;
run;
proc means data=a p20 p40 p60 p80;
var x;
run;
In a weighted analysis, the ECDF does not increase by 1/n at each datum. Instead, the ECDF increases by w[i]/W where W=sum_i w[i] is the sum of the weights. (This is equivalent to choosing weight that sum to 1, which would represent the proportion of weight for each datum.) Thus the unweighted percentile p is not necessarily equal to the weighted percentile for p. However, the extreme values (min=0th percentile; max=100th percentile) remain unchanged because they are the endpoints of the weighted ECDF, which still increases from 0 to 1.
For example, suppose you choose weights
x: 1, 2, 3, 4, 5, 6
wt: 0.3, 0.2, 0.05, 0.1, 0.3, 0.05
Then the following computation finds the weighted percentiles:
data Wt;
input x wt;
datalines;
1 0.3
2 0.2
3 0.05
4 0.1
5 0.3
6 0.05
;
proc means data=Wt p20 p40 p60 p80;
var x;
weight wt;
run;
The corresponding weighted ECDF looks like this:
To find the 20th weighted pctl, start at 0.2 on the Y axis. Go over until you hit the graph, then go down to get x=1.
To find the 40th weighted pctl, start at 0.4 on the Y axis. Go over until you hit the graph, then go down to get x=2
In a similar way, the 60th weighted pctl is x=4 and the 80th weighted pctl is x=5.
- Mark as New
- Bookmark
- Subscribe
- Mute
- RSS Feed
- Permalink
- Report Inappropriate Content
April 27 – 30 | Gaylord Texan | Grapevine, Texas
Registration is open
Walk in ready to learn. Walk out ready to deliver. This is the data and AI conference you can't afford to miss.
Register now and lock in 2025 pricing—just $495!
ANOVA, or Analysis Of Variance, is used to compare the averages or means of two or more populations to better understand how they differ. Watch this tutorial for more.
Find more tutorials on the SAS Users YouTube channel.