- Home
- /
- Analytics
- /
- Stat Procs
- /
- Re: Quantiles for Observations from a Triangular Distribution
- RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
- Mark as New
- Bookmark
- Subscribe
- Mute
- RSS Feed
- Permalink
- Report Inappropriate Content
The QUANTILE function lists several distributions but the TRIANGULAR distribution is not one of them. The RAND function can compute random variables from a triangular distribution. Suppose I have observations from a triangular distribution, how do I compute their quantiles? It's easy for distributions that the QUANTILE allows, but the triangle distribution isn't one of them. Any code is appreciated.
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- RSS Feed
- Permalink
- Report Inappropriate Content
@PaulN wrote:
Here's what I came up with. It seems to work.
data triangle_percentile;
set triangle;/*a=minimum, b=maximum, c=mode h =height*/
/*using the 1/2*base*height for a triangle */
/*and slope = (y2-y1)/(x2-x1), which is either */
/* h/(c-a) for x<=c or h/(b-c) for x > c */
/*the negative sign for the slope for the latter */
/is the minus sign after the 1. */
a=0;
b=1;
c=0.2;h=2;
if x <= c then
q= 0.5*(x-a)*(h/(c-a))*x;
else
q=1 - 0.5*(b-x)*(h/(b-c))*(1-x);
run;
Hello @PaulN,
Your algorithm correctly computes the values of the cumulative distribution function (CDF) from given quantiles. (For general values of a and b the formulas should read
q = 0.5*(x-a)*(h/(c-a))*(x-a)
and
q = 1 - 0.5*(b-x)*(h/(b-c))*(b-x)
respectively, but since a=0 and b=1 in your example, you get the correct results.)
But you set out to compute quantiles (from cumulative probabilities) like SAS's QUANTILE function -- the inverse function of the CDF. For that purpose @mkeintz's algorithm is correct.
For example, to answer the typical question "What is the 95% quantile of that triangular distribution?", his formula yields the 0.8 in the left column of your table from the 0.95 (=95%) in the right column:
1 - sqrt((1-0)*(1-0.2)*(1-0.95)) = 0.8
(mathematically; in SAS under Windows the result deviates from 0.8 by a tiny rounding error due to numeric representation issues).
- Mark as New
- Bookmark
- Subscribe
- Mute
- RSS Feed
- Permalink
- Report Inappropriate Content
Simulation and PROC UNIVARIATE?
or Calling @Rick_SAS
- Mark as New
- Bookmark
- Subscribe
- Mute
- RSS Feed
- Permalink
- Report Inappropriate Content
@PaulN wrote:
The QUANTILE function lists several distributions but the TRIANGULAR distribution is not one of them. The RAND function can compute random variables from a triangular distribution. Suppose I have observations from a triangular distribution, how do I compute their quantiles? It's easy for distributions that the QUANTILE allows, but the triangle distribution isn't one of them. Any code is appreciated.
Do you know the parameters of the trangular distribution? I.e. the minimum (a), maximum (b) and mode (c)?
If so, then according to https://github.com/distributions-io/triangular-quantile the formula for quantiles (q) of a triangular distribution is:
if p < (c-a)/(b-a) then q= a + sqrt((b-a)*(c-a)*p) ;
else q= b - sqrt((b-a)*(b-c)*(1-p)) ;
where
- p is the cumulative distribution level for which you want a quantile
and - (c-a)/(b-a) is the cumulative distribution at the mode value c (i.e. F(c) )
The hash OUTPUT method will overwrite a SAS data set, but not append. That can be costly. Consider voting for Add a HASH object method which would append a hash object to an existing SAS data set
Would enabling PROC SORT to simultaneously output multiple datasets be useful? Then vote for
Allow PROC SORT to output multiple datasets
--------------------------
- Mark as New
- Bookmark
- Subscribe
- Mute
- RSS Feed
- Permalink
- Report Inappropriate Content
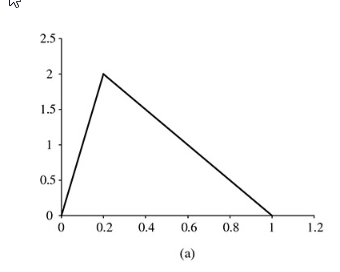
I do know the minimum (a), maximum (b), and mode (c).
minimum = 0
maximum = 1
mode = 0.2
Height of triangle = 2.
I'll use your code and see what I get. I'll compare it to my hand computations. Thank you for the help.
- Mark as New
- Bookmark
- Subscribe
- Mute
- RSS Feed
- Permalink
- Report Inappropriate Content
Here's the triangle distribution that I'm attempting to get SAS to compute quantiles. When I do it by hand I get the following but when I run the code it doesn't match. Any suggestions?
data triangle;
input x;
datalines;
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
;
run;
data triangle_percentile;
set triangle;
/*a=minimum, b=maximum, c=mode*/
a=0;
b=1;
c=0.2;
if x <= (c-a)/(b-a) then
q=a + sqrt((b-a)*(c-a)*x);
else
q=b - sqrt((b-a)*(b-c)*(1-x));
run;
- Mark as New
- Bookmark
- Subscribe
- Mute
- RSS Feed
- Permalink
- Report Inappropriate Content
Here's what I came up with. It seems to work.
data triangle_percentile;
set triangle;
/*a=minimum, b=maximum, c=mode h =height*/
/*using the 1/2*base*height for a triangle */
/*and slope = (y2-y1)/(x2-x1), which is either */
/* h/(c-a) for x<=c or h/(b-c) for x > c */
/*the negative sign for the slope for the latter */
/is the minus sign after the 1. */
a=0;
b=1;
c=0.2;
h=2;
if x <= c then
q= 0.5*(x-a)*(h/(c-a))*x;
else
q=1 - 0.5*(b-x)*(h/(b-c))*(1-x);
run;
- Mark as New
- Bookmark
- Subscribe
- Mute
- RSS Feed
- Permalink
- Report Inappropriate Content
@PaulN wrote:
Here's what I came up with. It seems to work.
data triangle_percentile;
set triangle;/*a=minimum, b=maximum, c=mode h =height*/
/*using the 1/2*base*height for a triangle */
/*and slope = (y2-y1)/(x2-x1), which is either */
/* h/(c-a) for x<=c or h/(b-c) for x > c */
/*the negative sign for the slope for the latter */
/is the minus sign after the 1. */
a=0;
b=1;
c=0.2;h=2;
if x <= c then
q= 0.5*(x-a)*(h/(c-a))*x;
else
q=1 - 0.5*(b-x)*(h/(b-c))*(1-x);
run;
Hello @PaulN,
Your algorithm correctly computes the values of the cumulative distribution function (CDF) from given quantiles. (For general values of a and b the formulas should read
q = 0.5*(x-a)*(h/(c-a))*(x-a)
and
q = 1 - 0.5*(b-x)*(h/(b-c))*(b-x)
respectively, but since a=0 and b=1 in your example, you get the correct results.)
But you set out to compute quantiles (from cumulative probabilities) like SAS's QUANTILE function -- the inverse function of the CDF. For that purpose @mkeintz's algorithm is correct.
For example, to answer the typical question "What is the 95% quantile of that triangular distribution?", his formula yields the 0.8 in the left column of your table from the 0.95 (=95%) in the right column:
1 - sqrt((1-0)*(1-0.2)*(1-0.95)) = 0.8
(mathematically; in SAS under Windows the result deviates from 0.8 by a tiny rounding error due to numeric representation issues).
- Mark as New
- Bookmark
- Subscribe
- Mute
- RSS Feed
- Permalink
- Report Inappropriate Content
Thanks for the clarification. I should have stated my problem differently. Your help is appreciated.
- Mark as New
- Bookmark
- Subscribe
- Mute
- RSS Feed
- Permalink
- Report Inappropriate Content
You're welcome. So, you really wanted to extend the CDF function to the triangular distribution, not the QUANTILE function mentioned in your initial post. (Otherwise mkeintz's reply, not my clarification, should be marked as the accepted solution.) Indeed, rereading your question "Suppose I have observations from a triangular distribution, how do I compute their quantiles?" it sounds like you start with observations x between a and b and want to compute cumulative probabilities p (which you denote with q), not vice versa.
April 27 – 30 | Gaylord Texan | Grapevine, Texas
Registration is open
Walk in ready to learn. Walk out ready to deliver. This is the data and AI conference you can't afford to miss.
Register now and save with the early bird rate—just $795!
ANOVA, or Analysis Of Variance, is used to compare the averages or means of two or more populations to better understand how they differ. Watch this tutorial for more.
Find more tutorials on the SAS Users YouTube channel.