- Home
- /
- Analytics
- /
- Stat Procs
- /
- PERT-sampling of data
- RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
- Mark as New
- Bookmark
- Subscribe
- Mute
- RSS Feed
- Permalink
- Report Inappropriate Content
I hope this question is admissible as it is not about SAS-syntax, but about the meaning of Rick_SAS's & Ksharp's line of code? The ifn-part, of course, is clear, I am looking for a substantial interpretation or a source of this formula:
_RATE_= ifn((prob<=&peak),prob,2*&peak-prob)
The complete program was:
%let peak=0.7;
title 'Simulation from Normal';
data normal;
call streaminit(1234);
do i=1 to 100000;
x=rand('normal');
prob = cdf("Normal", x);
_RATE_= ifn((prob<=&peak),prob,2*&peak-prob); * <-- distribution function of PERT?? ;
output;
end;
drop prob ;
run;
proc surveyselect data=normal out=want method=PPS_WR N=10000;
size _RATE_; /* specify the probability variable */
run;
proc sgplot data=want;
histogram x;
density x/type=kernel;
run;
The original post was:
Thanks&kind regards
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- RSS Feed
- Permalink
- Report Inappropriate Content
Xia wrote that, so you'll have to ask him what he was thinking. It looks like he was trying to specify the density for the triangular distribution on [0,1] with peak at &peak. However, the formula he gave is incorrect since it can become negative and doesn't integrate to 1.
If you want the density of the triangular distribution, use the following:
data Triangle;
do x = 0 to 1 by 0.01;
pdf = ifn((x<=&peak), 2*x/&peak, 2*(1-x)/(1-&peak));
output;
end;
run;
/* visualize distribution: should have peak at &peak */
proc sgplot data=Triangle;
series x=x y=pdf;
run;
- Mark as New
- Bookmark
- Subscribe
- Mute
- RSS Feed
- Permalink
- Report Inappropriate Content
Xia wrote that, so you'll have to ask him what he was thinking. It looks like he was trying to specify the density for the triangular distribution on [0,1] with peak at &peak. However, the formula he gave is incorrect since it can become negative and doesn't integrate to 1.
If you want the density of the triangular distribution, use the following:
data Triangle;
do x = 0 to 1 by 0.01;
pdf = ifn((x<=&peak), 2*x/&peak, 2*(1-x)/(1-&peak));
output;
end;
run;
/* visualize distribution: should have peak at &peak */
proc sgplot data=Triangle;
series x=x y=pdf;
run;
- Mark as New
- Bookmark
- Subscribe
- Mute
- RSS Feed
- Permalink
- Report Inappropriate Content
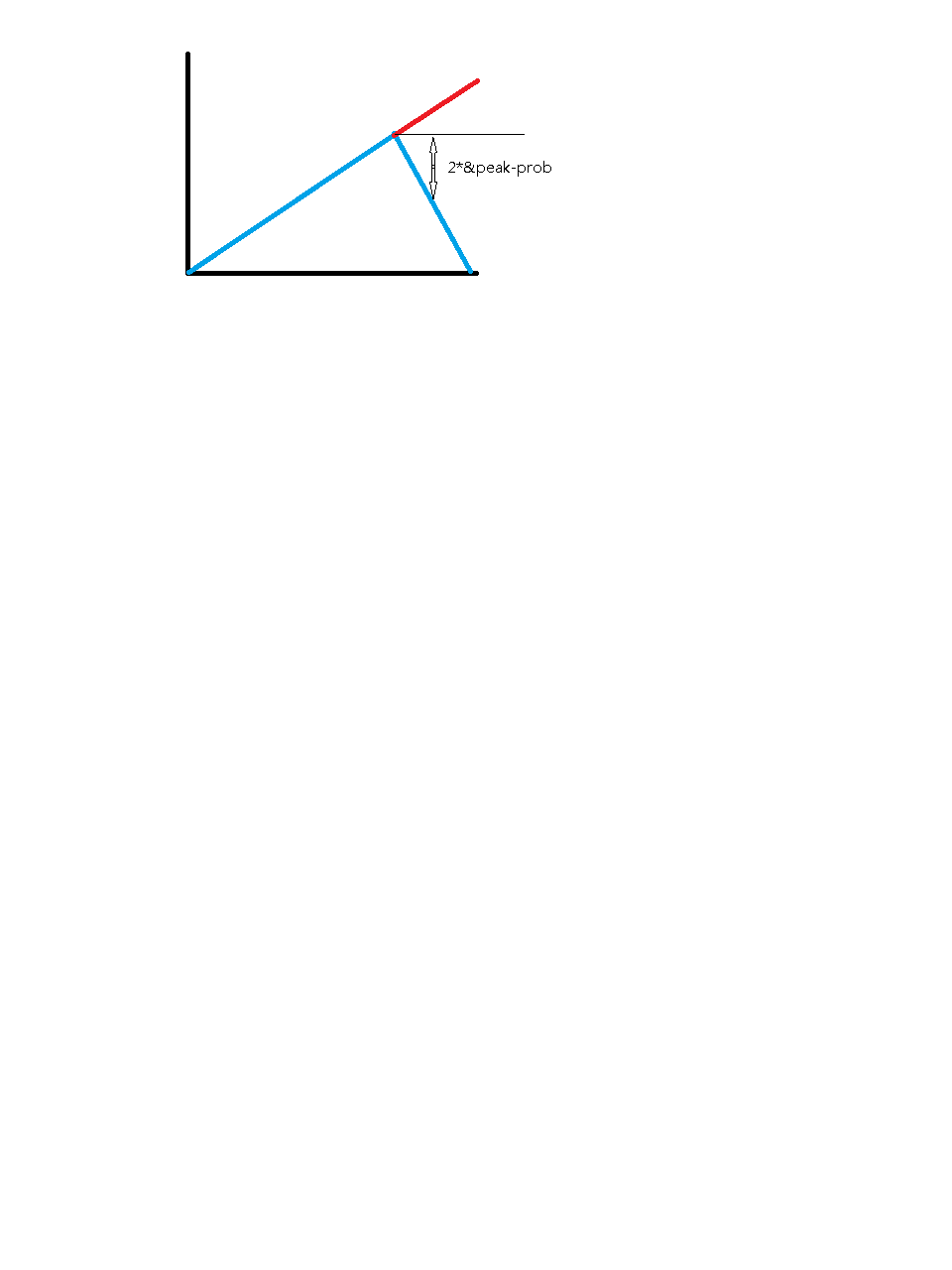
Yes. My function is not right only suited for peak=0.5 . What I am trying to do is this . And need new function to compute the sample prob of a value from Normal.
- Mark as New
- Bookmark
- Subscribe
- Mute
- RSS Feed
- Permalink
- Report Inappropriate Content
Rick's formula is right . Try this one .
%let peak=0.7;
title 'Simulation from Normal';
data normal;
call streaminit(1234);
do i=1 to 100000;
x=rand('normal');
prob = cdf("Normal", x);
if prob=&peak then _RATE_=2;
else _RATE_= ifn((prob<&peak), 2*prob/&peak, 2*(1-prob)/(1-&peak)); * <-- special sample prob for a value from normal;
output;
end;
drop prob ;
run;
proc surveyselect data=normal out=want method=PPS_WR N=10000;
size _RATE_; /* specify the probability variable */
run;
proc sgplot data=want;
histogram x;
density x/type=kernel;
run;
Edited
ANOVA, or Analysis Of Variance, is used to compare the averages or means of two or more populations to better understand how they differ. Watch this tutorial for more.
Find more tutorials on the SAS Users YouTube channel.