Minimal detectable change and test-rest variability

[obrien]

Hello,

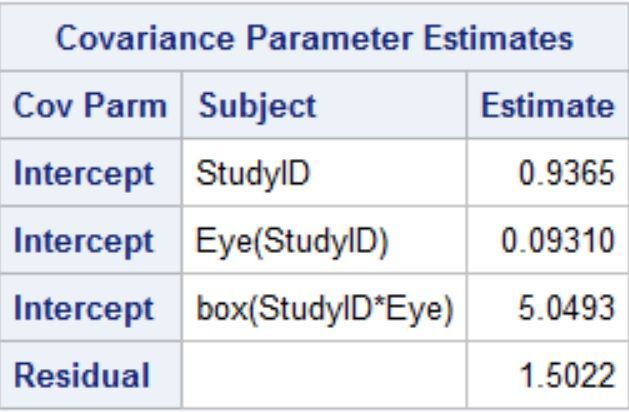
I need to establish the minimal detectable change for an outcome to distinguish true change from test-retest variability. The data has 30 eyes of 20 participants with 3 scans on the same day. A grid of 25 squares (boxes) is applied to each of the 3 scans and the outcome is obtained in each box for a total of 30×3×25 = 2250 observations. In the literature, minimal detectable change is defined as

MDC95 = sqrt(2)×1.96×SEM

where SEM is standard error of measurement and is the same as within subject (residual) standard deviation.

I am using the following SAS code

proc mixed data = dat method=REML;
   class StudyID Eye box;
   model y = / solution ddfm=kr;
   random intercept / subject=StudyID;
   random intercept / subject=Eye(StudyID);
   random intercept / subject=box(Eye StudyID);
run;

I think I have approached this correctly but I would definitely appreciate confirmation.

Thanks,

Robert

[awesome_opossum]

It's been awhile since I've done a model like this.  You have the first step correct, or at least workable.  You need add predictors to your y = model, and it may also be necessary to add random slopes for your "boxes", depending on model fit.