Logistic regression with spatial correlation

[buhl2752]

Hello,

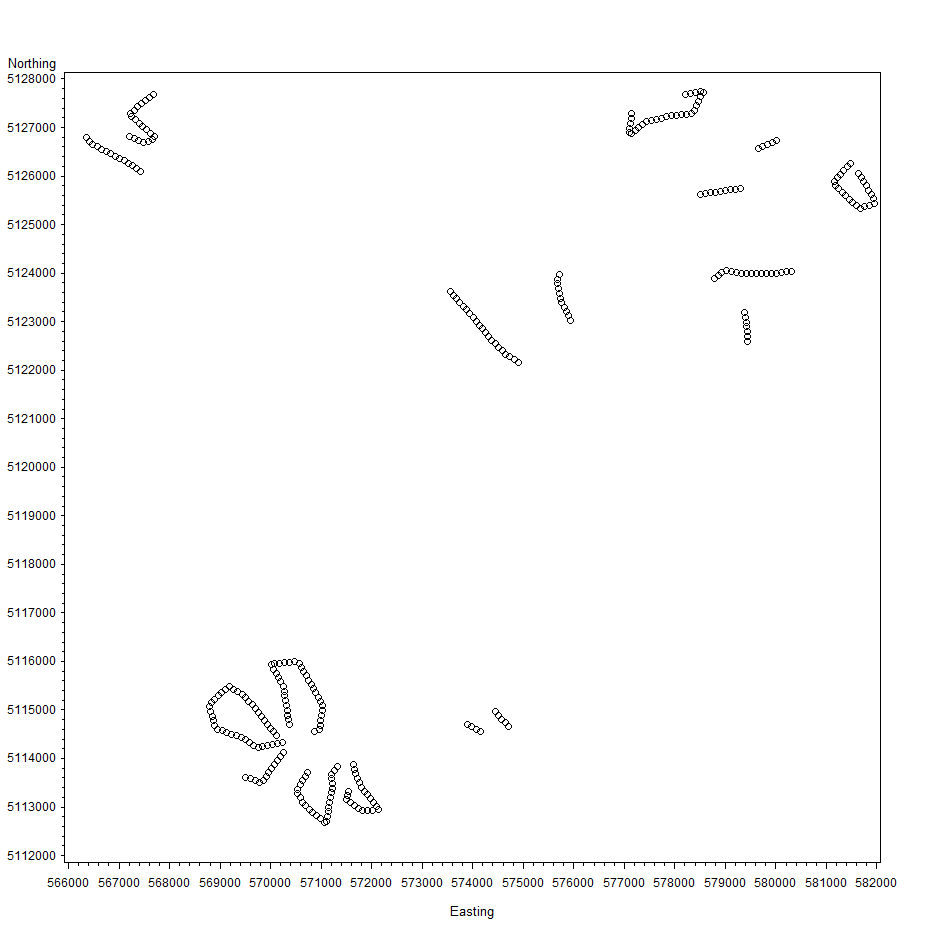
I am doing a logistic regression with random effects.  I have 300 segments within the study.  At each plot the presence or absence of a particular bird species is recorded along with many continuous covariates.  Because these segments are situated within transects (not necessarily straight transects, sometimes the end point is very close to the starting point) and some transects are very close (I attached a figure showing the location of the segments relative to each other in case it would help - each circle is a segment).  I am trying to account for spatial corrleation among all segments.  My model is as follows:

PROC GLIMMIX DATA=LCSP METHOD=LAPLACE MAXOPT=50 IC=PQ;

CLASS SEGMT;

MODEL PRESENT_50 = WTRDEP / DIST=BINOMIAL S DDFM=RESIDUAL;

RANDOM SEGMT / SUBJECT=INTERCEPT TYPE=SP(SPH)(EASTING NORTHING);

RUN;

I am modeling the spatial correlation as a g-side effect and using method=Laplace because I have 34 covariates and am trying to use AIC to compare models. 

My problem is that often the standard errors for the covariance parameters or the standard errors for the parameter estimates are missing.  In addition, sometimes the spatial covariance parameter is equal to zero.  The missing standard errors do not seem to be having a huge effect on the results, but I am concerned about the validity of these results.  On the other hand, when the spatial covariance parameter is equal to zero, the log likelihood is greatly affected and therefore so is the AIC value.  The log likelihood basically comes out about half of what it is for models where this covariance parameter is not zero, which in turn makes these models appear to be far superior models.

So obviously I am not doing somethiing right.  I have tried various other options that I thought would help with no luck.  The only thing that helped somewhat is to give starting parameter estimate values.  For about half the models that had a covariance parameter equal to zero, now didn't; but the other half of the models failed.  So I am not sure this is a solution or if I believe the results in this case either.

Not sure where to go from here.  Any help would be appreciated.

Thanks,

Deb

[SteveDenham]

Generally, the lack of standard errors for the covariance parameters is a symptom of an overspecified model.  In this case, I suspect that it is only "overspecified" to the extent that there is likely not enough data to support calculation of the parameters to the degree needed.

Maybe, and this is just a maybe, if you switched the RANDOM statement to:

random intercept/subject=segmt type=sp(sph)(easting northing);

things would work out, so that the correlation is modeled within each level of segmt, rather than across the entire dataset (which is what subject=intercept results in).  No guarantee though.

Steve Denham

[buhl2752]

Thanks Steve,

I only have one observations per sement so there is no within segment correlation to model, so changing the random statement is not going to achieve my goal.

However, I suspect that you are correct that the model is overspecified, and therefore resulting in missing standard errors.  Any thoughts on whether or not this would affect the log likelihood and susequently the AIC value?  I am not that interested in the parameter values themseleves (other than whether they are positive or negative) and am not looking at p-values.  My goal is to determine which of the many covariates may be having some influence (or have an association with) the response variable.

Deb

[SteveDenham]

If the algorithm converges, and there are no messages regarding the Hessian matrix or G matrix, then the log likelihood and information criteria values are probably in good shape.  You may want to check on this by providing different starting values in a PARMS statement, just to be sure that you are converging to a global extremum, rather than a local.  The latter is pretty likely with an overspecified model.

Steve Denham