- Home
- /
- Analytics
- /
- Stat Procs
- /
- Fisher's Exact Test Not Showing p-value
- RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
- Mark as New
- Bookmark
- Subscribe
- Mute
- RSS Feed
- Permalink
- Report Inappropriate Content
Hi, so I run a Fisher's exact test, and it shows me that the table probability is <0.0001, but doesn't show any other p-values like the one-sided or two-sided p-values
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- RSS Feed
- Permalink
- Report Inappropriate Content
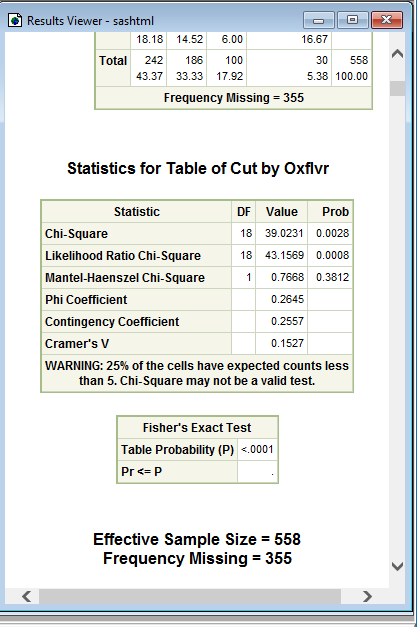
Your answer is in the WARNING.
WARNING: There is not enough memory available to compute Fisher's exact test.
The suggestion would be to either use the asymptotic test or get a Monte-Carlo estimate of the exact p-value by adding the MC option to the EXACT statement.
PROC FREQ DATA=first;
TABLES cut*Oxarma;
EXACT FISHER/MC:
RUN:
- Mark as New
- Bookmark
- Subscribe
- Mute
- RSS Feed
- Permalink
- Report Inappropriate Content
- Mark as New
- Bookmark
- Subscribe
- Mute
- RSS Feed
- Permalink
- Report Inappropriate Content
PROC FORMAT; value $Oxarma '1' = 'None' '2' = 'Trace' '3' = 'Some' '4' = 'Unacceptable'; value $Oxarmab '1' = 'None/Trace' '2' = 'None/Trace' '3' = 'Some' '4' = 'Unacceptable'; value $Oxarmac '1' = 'Acceptable' '2' = 'Acceptable' '3' = 'Acceptable' '4' = 'Unacceptable'; Run; PROC FREQ data=first; tables day*Oxarma / FISHER; format Oxarma $Oxarma.; Run; Quit;
Log:
PROC FREQ data=first;
946 tables cut*Oxarma / FISHER;
947 format Oxarma $Oxarma.;
948 Run;NOTE: Writing HTML Body file: sashtml.htm
WARNING: Computing exact p-values for this problem may require much time and memory. Press the
system interrupt key to terminate exact computations.
WARNING: There is not enough memory available to compute Fisher's exact test.
NOTE: There were 913 observations read from the data set WORK.FIRST.
NOTE: PROCEDURE FREQ used (Total process time):
real time 5:32.70
cpu time 5:28.39
- Mark as New
- Bookmark
- Subscribe
- Mute
- RSS Feed
- Permalink
- Report Inappropriate Content
Your answer is in the WARNING.
WARNING: There is not enough memory available to compute Fisher's exact test.
The suggestion would be to either use the asymptotic test or get a Monte-Carlo estimate of the exact p-value by adding the MC option to the EXACT statement.
PROC FREQ DATA=first;
TABLES cut*Oxarma;
EXACT FISHER/MC:
RUN:
- Mark as New
- Bookmark
- Subscribe
- Mute
- RSS Feed
- Permalink
- Report Inappropriate Content
Pr <= P 0.9481
99% Lower Conf Limit 0.9424
99% Upper Conf Limit 0.9538
Number of Samples 10000
Initial Seed 358024000
This is the data I get. How reliable is this Monte Carlo estimate? This suggests that the two variables are independent and that the treatment does not affect the outcome, does it not?
- Mark as New
- Bookmark
- Subscribe
- Mute
- RSS Feed
- Permalink
- Report Inappropriate Content
The MC estimate is very reliable. Interpretation in terms of treatment and outcome is left to the researcher. Only he/she knows the details of the data. For instance, why so many data are missing...
- Mark as New
- Bookmark
- Subscribe
- Mute
- RSS Feed
- Permalink
- Report Inappropriate Content
- Mark as New
- Bookmark
- Subscribe
- Mute
- RSS Feed
- Permalink
- Report Inappropriate Content
- Mark as New
- Bookmark
- Subscribe
- Mute
- RSS Feed
- Permalink
- Report Inappropriate Content

The 2025 SAS Hackathon has begun!
It's finally time to hack! Remember to visit the SAS Hacker's Hub regularly for news and updates.
ANOVA, or Analysis Of Variance, is used to compare the averages or means of two or more populations to better understand how they differ. Watch this tutorial for more.
Find more tutorials on the SAS Users YouTube channel.