- Home
- /
- Analytics
- /
- Stat Procs
- /
- Re: Exact logistic regression
- RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
- Mark as New
- Bookmark
- Subscribe
- Mute
- RSS Feed
- Permalink
- Report Inappropriate Content
Hi,
I want to perform exact logistic regression in SAS. I've found the following code that I want to apply to different samples of varying size.
(I use the university edition. )
PROC IMPORT DATAFILE=REFFILE
DBMS=DBF
OUT=WORK.IMPORT;
RUN;
proc logistic data = WORK.IMPORT desc;
model y = x1 x2;
exact x1 x2 / estimate = both;
run;
When I run this code I get empty tables with no estimates...
Must the data be written in a specific way, in that case, how?
I can perform ordinary logistic regression on the samples, and my goal is to compare the results.
I have attached the three files, log, results and data - that contains 20 observations. Because the files did not have the valid extension they are all in paint, sorry for that.
I'm grateful for all the help I can get.

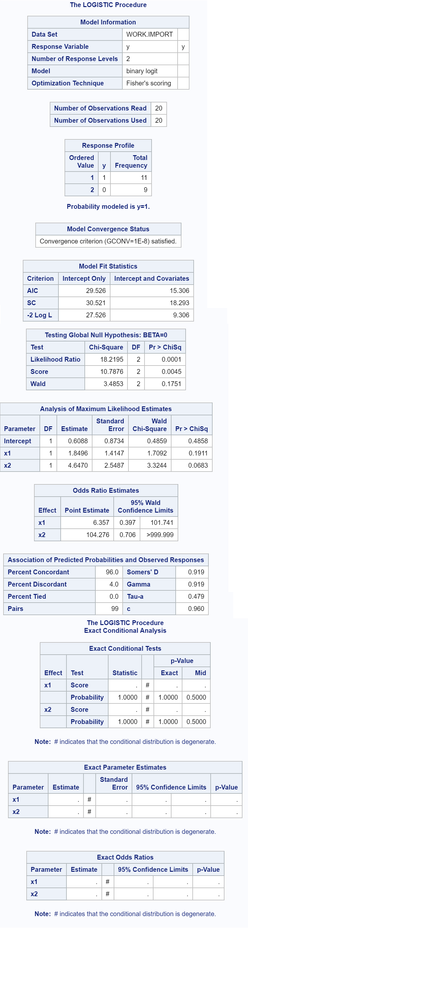

- Mark as New
- Bookmark
- Subscribe
- Mute
- RSS Feed
- Permalink
- Report Inappropriate Content
- Mark as New
- Bookmark
- Subscribe
- Mute
- RSS Feed
- Permalink
- Report Inappropriate Content
Post your data in the form of a data step, most people in here dont want to download files 🙂
- Mark as New
- Bookmark
- Subscribe
- Mute
- RSS Feed
- Permalink
- Report Inappropriate Content
My Data:
y x1 x2
1. 1 1.489611900786800 -0.486983894512530
2. 1 0.887638190472230 -0.899961461187430
3. 1 -0.328400349680380 0.320480850960210
4. 0 -1.283346136073470 0.314729922388780
5. 1 -0.014384666024895 -1.040793737862780
6. 1 1.005337941612940 0.385444205622100
7. 1 0.403112850999760 0.797554772638080
8. 1 1.432508077938930 -0.553701810045310
9. 1 0.137341139238340 0.177313212434980
10. 0 -1.341507064615280 0.042985039337917
Logg:
1 OPTIONS NONOTES NOSTIMER NOSOURCE NOSYNTAXCHECK;
61
62 PROC IMPORT DATAFILE=REFFILE
63 DBMS=DBF
64 OUT=WORK.IMPORT1;
65 RUN;
NOTE: Import cancelled. Output dataset WORK.IMPORT1 already exists. Specify REPLACE option to overwrite it.
NOTE: The SAS System stopped processing this step because of errors.
NOTE: PROCEDURE IMPORT used (Total process time):
real time 0.00 seconds
cpu time 0.00 seconds
66
67
68 proc logistic data = WORK.IMPORT1;
69 model y = x1 x2;
70 run;
NOTE: PROC LOGISTIC is modeling the probability that y=0. One way to change this to model the probability that y=1 is to specify
the response variable option EVENT='1'.
WARNING: There is a complete separation of data points. The maximum likelihood estimate does not exist.
WARNING: The LOGISTIC procedure continues in spite of the above warning. Results shown are based on the last maximum likelihood
iteration. Validity of the model fit is questionable.
NOTE: There were 10 observations read from the data set WORK.IMPORT1.
NOTE: PROCEDURE LOGISTIC used (Total process time):
real time 0.12 seconds
cpu time 0.12 seconds
71
72 proc logistic data = WORK.IMPORT1 desc;
73 model y = x1 x2;
74 exact x1 x2 /estimate=both;
75 run;
NOTE: PROC LOGISTIC is modeling the probability that y=1.
WARNING: There is a complete separation of data points. The maximum likelihood estimate does not exist.
WARNING: The LOGISTIC procedure continues in spite of the above warning. Results shown are based on the last maximum likelihood
iteration. Validity of the model fit is questionable.
NOTE: There were 10 observations read from the data set WORK.IMPORT1.
NOTE: PROCEDURE LOGISTIC used (Total process time):
real time 0.12 seconds
cpu time 0.12 seconds
76
77 OPTIONS NONOTES NOSTIMER NOSOURCE NOSYNTAXCHECK;
90
- Mark as New
- Bookmark
- Subscribe
- Mute
- RSS Feed
- Permalink
- Report Inappropriate Content
With only 10 observations in your posted dataset, split 2 and 8 between outcomes, I don't know that you'll be able to extract much from an analysis, but....
If you plot the response against each predictor, it is clear that complete separation is due to X1. A solution can be obtained using Firth's penalized likelihood. See
https://pdfs.semanticscholar.org/4f17/1322108dff719da6aa0d354d5f73c9c474de.pdf
and
http://support.sas.com/kb/22/599.html
data have;
input a$ y x1 x2;
datalines;
1. 1 1.489611900786800 -0.486983894512530
2. 1 0.887638190472230 -0.899961461187430
3. 1 -0.328400349680380 0.320480850960210
4. 0 -1.283346136073470 0.314729922388780
5. 1 -0.014384666024895 -1.040793737862780
6. 1 1.005337941612940 0.385444205622100
7. 1 0.403112850999760 0.797554772638080
8. 1 1.432508077938930 -0.553701810045310
9. 1 0.137341139238340 0.177313212434980
10. 0 -1.341507064615280 0.042985039337917
;
run;
proc sgplot data=have;
scatter x=x1 y=y;
run;
proc sgplot data=have;
scatter x=x2 y=y;
run;
proc logistic data = have desc;
model y = x1 x2 / firth;
run;
ANOVA, or Analysis Of Variance, is used to compare the averages or means of two or more populations to better understand how they differ. Watch this tutorial for more.
Find more tutorials on the SAS Users YouTube channel.



