Classification Accuracy Discrepancy (between raw calculation and proc logistic)

[H]

I have a single dependent variable (binary) and a single independent variable (binary). When I calculate the variable's accuracy for predicting the outcome by hand, (TP+TN) / (TP + TN + FP + FN) = 0.69.

Though, when running data through proc logistic the accuracy (c-statistic) = 0.58.

What is the cause of this discrepancy? Is it related to maximum likelihood and the usee of sparse data for some subgroupings? This is for a medical diagnostic, so I want the hand calculation value and 95% CI from the logistic model. However the accuracy values are different. I have attached some code to convey this issue.

%let N = 129;
%let P = 0.372;
%let SN = 0.1875;
%let SP = 0.98765;
Data diagnostic;
	Col1 = &N * &P;
	Col2 = &N - Col1;
	TP = Col1 * &SN;
	FN = Col1 - TP;
	TN = Col2 * &SP;
	FP = Col2 - TN;
	Accuracy = (TP + TN) / (TP + FP + FN + TN);
	do j= 1 to TP;
		exposure = 1; 
		outcome = 1; 
		output;
	end;
	do j= 1 to FP;
		exposure = 1; 
		outcome = 0; 
		output;
	end;
	do j= 1 to FN;
		exposure = 0; 
		outcome = 1; 
		output;
	end;
	do j= 1 to TN;
		exposure = 0; 
		outcome = 0; 
		output;
	end;
	keep exposure outcome Accuracy;
run;
proc print data=diagnostic;
	var accuracy;
run;
ods output ROCAssociation=Estimates;
proc logistic data=diagnostic;
	class 	exposure (ref='0') / param=ref;
	model outcome (event='1') =  exposure / lackfit;
	roc 'CIs' exposure; /*c CI*/
run;

P.S., the values are so different the 95% CI for the logistic derived value exclude the hand calculated value for accuracy

[ballardw]

Do any of the variables used on the model statement have missing values? The model will exclude those records.

Look in the proc output for the number of records used and compare that to the number of records in your data set.

[H]

I don't believe it will be that easy. I provided an example, which if ran, you can see both have n=127. Also, I would imagine that it would take a sufficient amount of missing data to shift accuracy down by > 10%.

[FreelanceReinh]

The main reason for the discrepancy is that you are dealing with two different statistics: accuracy (your hand calculation) and concordance index c (=area under the ROC curve, computed by PROC LOGISTIC).

The accuracy estimates the probability of a correct prediction (outcome 1 or 0) for a single, randomly selected subject. This assumes a fixed decision rule.

In contrast, the concordance index estimates the probability that for a pair of individuals, randomly selected from the set of all pairs combining one subject with outcome 1 and one with outcome 0, the estimated probabilities for "outcome=1" and the actual outcomes are concordant. This statistic does not assume a fixed decision rule.

I can add more details tomorrow, if you like.

Another issue with your calculation are rounding errors leading to N=127 observations in your analysis dataset, although you had started with N=129.

[H]

Yes, please add more. I appreciate all feedback. Yeah, I was trying to recall the concordance index, I remembered you grabbed one of each, but did not recall the membership component. The slight predicament I had found myself in was just the reporting of the results, since I report SEN and SPEC, which didn't jive with the model.

I guess what I was thinking, was you always hear the AUC and C-statistic are the same. However the AUC is based on the SEN and SPEC, but as you elucidated the c-index is not, I guess it comes back to the scoring of variables from the ML model.

I was also trying to remember, how you get at the final value of the c-index. Is it the accuracy after comparing every possible combination of the 0s and 1s probability values? So the 1s should have a probability greater than the Os 58% of the time, given the logistic model?

Yes, I saw the basic simulation code I used botch the n-value, but I was looking past it since I calculated the hand-version and logistic, with just the 127 observations. So they were both corrumpted!!

Thanks.

[FreelanceReinh]

The denominator of your hand-calculated accuracy is 129 (up to very minor rounding issues). The N=127 in dataset DIAGNOSTIC is due to the end values of the first and third DO loop: TP=8.99775, FN=38.99025, which are truncated to 8 and 38, resp. If these are rounded properly to 9 and 39, resp., we obtain the following 2x2 contingency table:

Table of exposure by outcome

exposure     outcome

Frequency|
Percent  |
Row Pct  |
Col Pct  |       0|       1|  Total
---------+--------+--------+
       0 |     80 |     39 |    119
         |  62.02 |  30.23 |  92.25
         |  67.23 |  32.77 |
         |  98.77 |  81.25 |
---------+--------+--------+
       1 |      1 |      9 |     10
         |   0.78 |   6.98 |   7.75
         |  10.00 |  90.00 |
         |   1.23 |  18.75 |
---------+--------+--------+
Total          81       48      129
            62.79    37.21   100.00

Using the decision rule "if exposure=0, then predict outcome=0; if exposure=1, then predict outcome=1," we get:

sensitivity =  9/48  = 0.1875
specificity = 80/81  = 0.98765... 
accuracy    = 89/129 = 0.68992...

The maximum likelihood parameter estimates for the logistic regression model with exposure as the only predictor reflect the probabilities which we already see in the 2x2 table:

Parameter     Estimate    

Intercept      -0.7185
exposure  1     2.9157

logistic(-0.7185) = 0.3277
logistic(-0.7185+2.9157) = 0.9000
(both rounded to 4 decimals, not an exact equality in the second case)

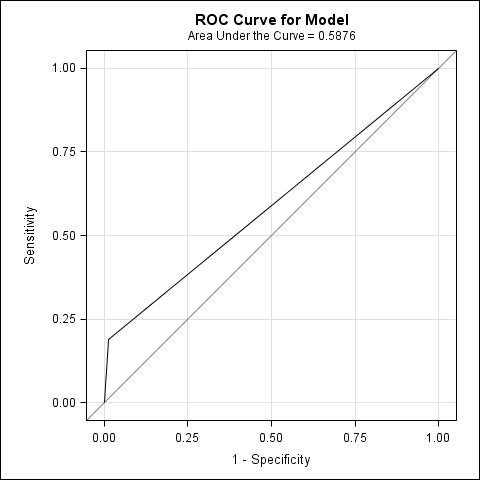
PROC LOGISTIC also creates the ROC curve (with ods graphics on;), which is a 3-point polygon with vertices at
(0, 0), (1/81, 9/48) and (1, 1).

Elementary calculation yields its area under the curve (AUC) as 4569/7776=0.58757... (the sum of two triangular areas and one rectangular area).

Now, let's consider all pairs of subjects in the analysis dataset which consist of one subject with outcome 1 and one with outcome 0.
There are 48*81=3888 such pairs.

Clearly concordant are those 9*80 pairs comprising one subject with exposure=outcome=1 and one with exposure=outcome=0, because the estimated probabilities from the model for outcome=1 are 0.9000 > 0.3277. If one pair is randomly selected from the set of 3888 pairs described above, the probability of catching one of those 720 pairs is 720/3888.

The 9*1+39*80=3129 pairs with equal exposure in both components are "borderline" cases with equal estimated probabilities. Their probability (in the drawing of pairs) is weighted by 1/2. The remaining 39*1 pairs are discordant (estimated probabilities 0.3277 < 0.9000).

So, the concordance index is calculated as
c = 720/3888 + (1/2)*3129/3888 = 4569/7776 = 0.58757..., exactly the AUC.

As the ROC curve joins points corresponding to a whole range of possible decision rules (cutpoints, pairs of sensitivity and specificity), the AUC, i.e. the concordance index c, is a statistic which does not depend on a particular decision rule -- unlike the accuracy.

[Edit 2019-04-30: Reattached plot, which had been deleted by mistake.]

[H]

Freelance,

You provided a great reply. In particular,  I appreciated how the c-index gets calculated. I also, liked the reference of how  the beta coefficients equaled the values in the classification table (which I had not checked). Lastly, your post was also very aethetically pleasing.

I guess for my quandary related to reporting the SEN and SPEC, but feeling if if I report the c-index from logistic - readers will be like me and say "hey, that is not the same value I can calculate for accuracy". I am looking for some insight in moving forward. I was planning to plot the accuracy values for the different cutoffs for the predictor (original continuous variable that I had created a threshold for in this example). The graph would look much like the ones you can see in linear models where they plot MSE changes for different modeling techniques.

I was also going to incorporate CI bands on the graph, which I can get from the logistic model, and via bootstrapping in the hand calculations. I guess regardless of how I progress, is there a proper use of terminology that I am missing. So I should use accuracy  if I do it by hand and use concordance index or AUC if I use the logistic model?  The logistic model seems like the better approach for the future, in that is provides an opportunigy to control for covariates in the model, if desired.

Any suggestions on  how to word the presentation of these data would be appreciated. I guess I was confused by how the SEN/(1-SPEC) is call accuracy and people also call the c-statistic the model accuracy.

THANKS!

[FreelanceReinh]

You're welcome.

The concordance index or AUC can be regarded as a measure of "overall diagnostic accuracy" (cf. this paper) across the whole range of possible threshold values (e.g. of a continuous predictor).

When I worked on a project about diagnostic tests, the focus was on AUC, not on accuracy for a specific threshold value. The reason was probably, that the main interest was in the general suitability of the (newly discovered biochemical) quantity to be measured.

I think, if you are already at the stage where decision rules (threshold values) are fixed, the accuracy (and of course sensitivity and specificity) will gain importance.

I don't really see a fundamental distinction between measures calculated by hand and measures coming from a logistic model. As demonstrated in my previous post, the concordance index from PROC LOGISTIC could very well be calculated manually (thanks to the simple form of the ROC curve).

So, in the presentation you could start with the AUC (concordance index), the "big picture," and later focus on a cutpoint (threshold value) of particular interest (e.g. one that satisfies an optimality criterion) and present sensitivity, specificity and accuracy for that. Positive and negative predictive values (which depend on the prevalence!) will likely be of interest, too.

In all cases, confidence intervals will be important additions to the point estimates. Also, the impact of the group sizes on accuracy (unlike sensitivity and specificity) should be considered.