- Home
- /
- Analytics
- /
- Stat Procs
- /
- Re: Bayesian TTest by Proc MCMC
- RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
- Mark as New
- Bookmark
- Subscribe
- Mute
- RSS Feed
- Permalink
- Report Inappropriate Content
This t-Test is taken from Statistical Business Analysis Using SAS
libname sasba 'c:\sasba\ames';
data ames;
set sasba.ames300;
run;
proc format;
value yesno 0=No 1=Yes;
run;
proc ttest data =ames plots (only)=qq alpha=.05 h0=0;
class bonus;
var gr_liv_area;
format bonus yesno.;
run;
Let's imagine we want to repeat the test using Bayes, in BUGS we could approach/reproduce! that result with this model.
model {
for (i in 1:2) {
mu[i] ~ dnorm(0.0,1.0E-6)
tau[i] ~ dgamma(0.001,0.001)
}
for (i in 1:n) {
area[i] ~ dnorm(mu[bonus[i]+1],tau[bonus[i]+1])
}
x1 ~ dnorm(mu[1],tau[1])
x2 ~ dnorm(mu[2],tau[2])
dx<- x1-x2
dmu<-mu[1]-mu[2]
}
list(
area = c(864, 1829, 1328, 1063, 2207, 972, 912, 1978, 1801, 2018, 882, 1370, 1350, 2402, 1600, 2020, 1629, 2452, 2490, 1114, 864, 1740, 1728, 1313, 1154, 1113, 1567, 1392, 1144, 1478, 1297, 1062, 1121, 1092, 1513, 1368, 1560, 1680, 2036, 1641, 874, 1782, 2464, 1574, 1460, 1175, 1740, 925, 1136, 1092, 1100, 1196, 1044, 825, 1117, 882, 1211, 1524, 1094, 1418, 924, 1445, 1091, 1279, 923, 816, 914, 872, 2633, 1636, 988, 1093, 1214, 1150, 912, 1442, 1721, 922, 948, 952, 1242, 897, 955, 1299, 998, 1342, 1442, 1500, 907, 1214, 768, 1839, 1680, 1696, 1478, 2279, 1240, 1040, 1293, 1868, 1780, 2156, 1334, 1251, 1216, 1124, 884, 1045, 1073, 1159, 1458, 1124, 1654, 1339, 720, 1068, 1296, 1022, 952, 875, 520, 838, 672, 816, 778, 968, 960, 1047, 694, 1103, 693, 641, 865, 884, 1108, 1616, 1536, 1962, 1154, 1668, 1374, 1461, 1328, 1324, 1412, 1112, 1716, 1529, 1672, 1406, 1079, 1376, 924, 1846, 1174, 1635, 1274, 1409, 1316, 1382, 1362, 1426, 1123, 1717, 1312, 1466, 1440, 1176, 1324, 1635, 1221, 1595, 1629, 3279, 1960, 1733, 2599, 1845, 1352, 3222, 1392, 1274, 1797, 2673, 1868, 2224, 1432, 1594, 2365, 2450, 2122, 1730, 2090, 2142, 1352, 1683, 2020, 1764, 1779, 1660, 2034, 1961, 2237, 1638, 2332, 1456, 1720, 1792, 2322, 2125, 1933, 1737, 1978, 1796, 1611, 2022, 2200, 1852, 2031, 1764, 1710, 1582, 1656, 1600, 1642, 2030, 1877, 2643, 2758, 2551, 2385, 2398, 2531, 2538, 2154, 2080, 1812, 2654, 2127, 1958, 1873, 1308, 1796, 1668, 2090, 1797, 1408, 1756, 1501, 2263, 1574, 1914, 1509, 1414, 1976, 1911, 1499, 1995, 1724, 2315, 2519, 1560, 1482, 1768, 1427, 1369, 1344, 2168, 2358, 1086, 2601, 1660, 1824, 1355, 1098, 1428, 2009, 1436, 1784, 2104, 1374, 1152, 1034, 1382, 1472, 1374, 1430, 2071, 1166, 1165, 1350, 1656, 954, 996, 965, 768, 1034, 898, 999, 1291),
bonus = c(0, 1, 0, 0, 1, 0, 0, 1, 1, 1, 0, 0, 0, 1, 1, 1, 1, 1, 1, 0, 0, 1, 1, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 1, 1, 1, 0, 1, 1, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 1, 0, 1, 0, 0, 0, 0, 0, 0, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 0, 0, 0, 1, 0, 1, 1, 1, 0, 0, 0, 1, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 1, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 1, 1, 0, 1, 0, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 0, 1, 1, 0, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 0, 1, 0, 0, 1, 1, 1, 1, 1, 1, 1, 0, 0, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 0, 0, 0, 1, 1, 1, 0, 1, 1, 1, 1, 0, 1, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 1, 0, 0, 0, 1, 0, 0, 0, 1, 1, 0, 1, 1, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0),
n=300
)
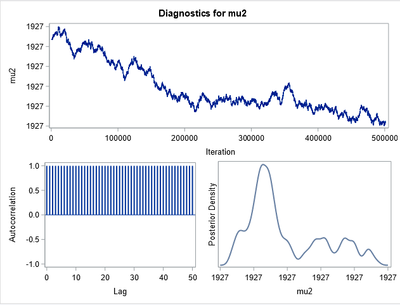
My problem is that when I try to reproduce this in Proc MCMC I get crazy results, without converge and in the autocorrelation I have zebra patterns. I think* the problem is in
model area ~ dnorm(mu[bonus+1],tau[bonus+1])
I say I think because the log is clean and all I have is my suspicion that mu[1] and tau[1] fail when bonus=1 and mu[2] and tau[2] fail when bonus=0. A failure is understood as not taking the record as null and ignoring it.
If someone has any idea, I would appreciate it.
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- RSS Feed
- Permalink
- Report Inappropriate Content
If you arrange your data in long format, with each record as bonus and then area, the following code is a start on the Bayesian t test in PROC MCMC:
proc mcmc data=your_data outpost=postout seed=123
nmc=40000 monitor=(_parms_ mudif)
statistics(alpha=0.01);
ods select PostSumInt; /* This may need to be commented out if you want all the diagnostics, etc. */
parm mu0 0 mu1 0;
parm sig20 1;
parm sig21 1;
prior mu: ~ general(0);
prior sig20 ~ general(-log(sig20), lower=0);
prior sig21 ~ general(-log(sig21), lower=0);
mudif = mu0 - mu1;
if bonus = 1 then do;
mu = mu1;
s2 = sig21;
end;
else do;
mu = mu0;
s2 = sig20;
end;
model area ~ normal(mu, var=s2);
run;
In this example, mu0 and sig20 are the mean and variance for bonus=0 and mu1 and sig21 are the mean and variance for bonus=1.
Now as far as how MCMC handles missing data: There is a section in the Details: MCMC Procedure folder for PROC MCMC documentation that covers everything about missing data. Key point 1 - there was a big change in how MCMC handles missing data implemented for all versions after SAS/STAT 9.3. In the earlier versions, MCMC could only model complete cases. Now there are at least four different methods, with each appropriate for various types of missing data models.
For MNAR data, the suggested approach is to fit more than one MODEL statement depending on whether you fit a conditional or marginal model to the response and the opposite type of model to the missingness vector.
I hope this is more in line with the question you posed.
SteveDenham
- Mark as New
- Bookmark
- Subscribe
- Mute
- RSS Feed
- Permalink
- Report Inappropriate Content
Google search:
bayesian t-test site:communities.sas.com
Koen
- Mark as New
- Bookmark
- Subscribe
- Mute
- RSS Feed
- Permalink
- Report Inappropriate Content
this is, the right way to translate from BUGS to SAS/MCMC.The t-test is
just one example of the problem with different management of missing/NA in
BUGS and missing/. In SAS.
Greetings
- Mark as New
- Bookmark
- Subscribe
- Mute
- RSS Feed
- Permalink
- Report Inappropriate Content
Can you enlighten those of us who have no BUGS experience as to the difference the missing values treatment?
Perhaps the issue has nothing to do with procedure but data preparation.
- Mark as New
- Bookmark
- Subscribe
- Mute
- RSS Feed
- Permalink
- Report Inappropriate Content
Well, there is little to explain, due to the attached "zebra" image and the code (alternate input data for one distribution/model and another), added to the fact that this code in BUGS yields the same result as in the referred book, We can only think that SAS "feeds" each distribution/model (statement) for each record in the input database. In other words, you cannot include MODEL in an IF-THEN and you cannot simulate it with indexes (as in the attached code) nor by transposing and completing with missing.
- Mark as New
- Bookmark
- Subscribe
- Mute
- RSS Feed
- Permalink
- Report Inappropriate Content
Would you care to share your MCMC code, and the dataset in sas7bdat format?
Additionally, there are at least two other PROCs that are capable of providing a Bayesian analysis of this sort - GENMOD and BGLIMM. Also, the documentation for the Behrens-Fisher problem in the MCMC Getting Started may be of assistance. For me, trying MCMC as a first step was a bit like trying to outrun Usain Bolt when I was just learning to walk.
SteveDemja,
- Mark as New
- Bookmark
- Subscribe
- Mute
- RSS Feed
- Permalink
- Report Inappropriate Content
deserves the grade of complicated/Olympic test (for Usain) when you will
not find anything more simple than it in the Volume I of examples of
WinBUGS. Indeed, it can be done by others proc-edures and I know how to
make it so, but the point is that I like to test my results with BUGS (it
forces me to make a second model, think it twice) and all what I wanted was
to make that test in SAS with proc MCMC, but it is not a drama keep making
it in R if SAS cannot. Regarding the code, let's make it easier, I just
need to know how to "include" a MODEL statement in a IF-THEN (proc MCMC). I
know it is not allowed, for that reason I wrote "include", the point is
that if I try to simulate it with the variable in MODEL missing, but it
results in a catastrophe (it is processed as a very low value) and not
skipped as happen with NA in BUGS. Thanks anyway.
- Mark as New
- Bookmark
- Subscribe
- Mute
- RSS Feed
- Permalink
- Report Inappropriate Content
If you arrange your data in long format, with each record as bonus and then area, the following code is a start on the Bayesian t test in PROC MCMC:
proc mcmc data=your_data outpost=postout seed=123
nmc=40000 monitor=(_parms_ mudif)
statistics(alpha=0.01);
ods select PostSumInt; /* This may need to be commented out if you want all the diagnostics, etc. */
parm mu0 0 mu1 0;
parm sig20 1;
parm sig21 1;
prior mu: ~ general(0);
prior sig20 ~ general(-log(sig20), lower=0);
prior sig21 ~ general(-log(sig21), lower=0);
mudif = mu0 - mu1;
if bonus = 1 then do;
mu = mu1;
s2 = sig21;
end;
else do;
mu = mu0;
s2 = sig20;
end;
model area ~ normal(mu, var=s2);
run;
In this example, mu0 and sig20 are the mean and variance for bonus=0 and mu1 and sig21 are the mean and variance for bonus=1.
Now as far as how MCMC handles missing data: There is a section in the Details: MCMC Procedure folder for PROC MCMC documentation that covers everything about missing data. Key point 1 - there was a big change in how MCMC handles missing data implemented for all versions after SAS/STAT 9.3. In the earlier versions, MCMC could only model complete cases. Now there are at least four different methods, with each appropriate for various types of missing data models.
For MNAR data, the suggested approach is to fit more than one MODEL statement depending on whether you fit a conditional or marginal model to the response and the opposite type of model to the missingness vector.
I hope this is more in line with the question you posed.
SteveDenham
- Mark as New
- Bookmark
- Subscribe
- Mute
- RSS Feed
- Permalink
- Report Inappropriate Content
Thanks Mr Steve Denham, you are Olympian to me
I checked the book, BUGS and your solution and I love it THANKS
April 27 – 30 | Gaylord Texan | Grapevine, Texas
Registration is open
Walk in ready to learn. Walk out ready to deliver. This is the data and AI conference you can't afford to miss.
Register now and save with the early bird rate—just $795!
ANOVA, or Analysis Of Variance, is used to compare the averages or means of two or more populations to better understand how they differ. Watch this tutorial for more.
Find more tutorials on the SAS Users YouTube channel.