- Home
- /
- Analytics
- /
- Stat Procs
- /
- Analyzing count data in GLIMMIX
- RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
- Mark as New
- Bookmark
- Subscribe
- Mute
- RSS Feed
- Permalink
- Report Inappropriate Content
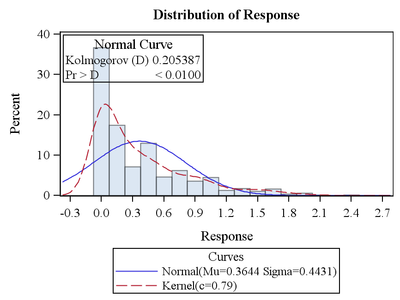
Hi, I need help in analyzing my count data (number of green leaves at maturity) measured from an experiment laid out in RCB with variety as a fixed factor and rep as a random factor. I know I need to run this in GLIMMIX but don't know how to go about analyzing this type of dataset with lots of zero values. I took a shot at using a negative binomial distribution, but the model did not converge (note log message: Pseudo-likelihood update fails in outer iteration 33). I then included method=laplace in the GLIMMIX statement, and this time the model converged but no estimates were given for the SE of the covariance parameters (not sure how to interpret that). I am a bit groping in the dark here as it's my first time to analyze such data in GLIMMIX.
I included here the SAS code that I used, a sample data and the distribution of my data for your reference.
Any help would be highly appreciated!
Proc GLIMMIX data= CountData plots=StudentPanel MAXLMMUPDATE=1000 MAXOPT=1000 ABSPCONV=.0000001
method=laplace;
class Rep var;
model response = var /dist=negbin;
random Rep;
lsmeans var /CL ILINK;
run;
- Tags:
- count data
- glimmix
- Mark as New
- Bookmark
- Subscribe
- Mute
- RSS Feed
- Permalink
- Report Inappropriate Content
Did you try Zero-Inflated Models ?
- Mark as New
- Bookmark
- Subscribe
- Mute
- RSS Feed
- Permalink
- Report Inappropriate Content
I wanted to, but don't know how to program it in GLIMMIX 😞
- Mark as New
- Bookmark
- Subscribe
- Mute
- RSS Feed
- Permalink
- Report Inappropriate Content
Could you switch it into proc genmod ?
- Mark as New
- Bookmark
- Subscribe
- Mute
- RSS Feed
- Permalink
- Report Inappropriate Content
Maybe, it is not unlikely that there will be many zero-values even if data comes from a Poisson distribution. The random effect will do that in many groups the expected value can be very low.
Changing to Poisson will increase chance for convergence alot, as the problem most likely is that the model has difficulties with distinguish the variance in the neg-bin distribution from the variance from the random effect.
Then, remember to be aware how you calculate the degrees of freedom, as it has a large impact on the p-values. I think the option "DDFM=BETWITHIN" is the best choiche when focus is on the fixed effect.
- Mark as New
- Bookmark
- Subscribe
- Mute
- RSS Feed
- Permalink
- Report Inappropriate Content
You have to be careful in the coding of the data. If rep is corresponding to each unique subject, then there would be confounding of the rep variance and the negative binomial (NB) scale parameter. You could not have both (either rep with Poisson, or NB and no rep). If "rep" corresponds to "blocks", so that there are different groups (e.g., treatments) all with the same rep level value, than it should work (no confounding). You didn't give enough output to identify the problem. Having a lot of zeros can happen when there is a NB or when there is a Poisson with a large random effect variance.
April 27 – 30 | Gaylord Texan | Grapevine, Texas
Registration is open
Walk in ready to learn. Walk out ready to deliver. This is the data and AI conference you can't afford to miss.
Register now and save with the early bird rate—just $795!
ANOVA, or Analysis Of Variance, is used to compare the averages or means of two or more populations to better understand how they differ. Watch this tutorial for more.
Find more tutorials on the SAS Users YouTube channel.