- Home
- /
- Programming
- /
- Programming
- /
- Reversing a Pvalue
- RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
- Mark as New
- Bookmark
- Subscribe
- Mute
- RSS Feed
- Permalink
- Report Inappropriate Content
Hello,
Using SAS 9.4, I want to calculate how many events would have to change from positive to negative to change a pvalue in a binary outcome. So, I have a binary outcome, disease, that is statistically significant (0.04); I want to know how many of the disease-yes would have to change to disease-no in order for the pvalue to become non-significant (0.05). Likewise, I would calculate the reverse of this where the pvalue is not significant and calculate how many disease-no would have to change to disease-yes to become significant.
Does anyone have an efficient way in SAS to perform this? Thank you
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- RSS Feed
- Permalink
- Report Inappropriate Content
Sure. Only output the records where the pValue <= 0.05 that are in the left tail:
/* find the largest number of events in the left tail for which
the p-value is less than 0.05. If desired, add "# events changed" column */
data SolnLeftTail;
set FisherOut(rename=(nValue1=pValue));
by Study;
retain foundMax;
if first.study then do;
maxLeftEvents = .;
foundMax = 0;
end;
if NOT foundMax then do;
if pValue <= 0.05 then do;
maxLeftEvents = x;
output;
end;
else
foundMax = 1;
end;
run;
proc print data=SolnLeftTail;
var Study x pValue;
run;in the left tail of each study. I'll let you figure out the "# of events changed" column:
- Mark as New
- Bookmark
- Subscribe
- Mute
- RSS Feed
- Permalink
- Report Inappropriate Content
Without knowing the exact statistical test you have performed, I can't be specific.
But you could certainly program a loop in a data step to increase/decrease the number of no responses and/or increase/decrease the number of yes responses to see what effect it has on the p-value.
Paige Miller
- Mark as New
- Bookmark
- Subscribe
- Mute
- RSS Feed
- Permalink
- Report Inappropriate Content
The test is a Chi Square or Fisher's exact.
Would you have an example of what a loop like that would look like? Thank you
- Mark as New
- Bookmark
- Subscribe
- Mute
- RSS Feed
- Permalink
- Report Inappropriate Content
More specific information is needed.
Do you mean a one-way table chi-squared test? Which is really a binomial test of proportions?
Do you mean a two-way table chi-squared test?
Do you mean something else?
Paige Miller
- Mark as New
- Bookmark
- Subscribe
- Mute
- RSS Feed
- Permalink
- Report Inappropriate Content
Is this for a 2x2 table? For example, Disease (No/Yes) as a response to clinical ARM (Control/Experimental)?
If so, Fisher's exact test enumerates all tables that have the observed row sums and column sums while fixing the sample size. Thus, there are three constraints for the four cells in the table. You can easily enumerate all tables by considering 0, 1, ..., n for the first cell and then using the constraints to fill in the other cells.
The probability for these tables follows a hypergeometric distribution, so you can compute the probability of each case. the parameters of the hypergeometric distribution are
N = sample size
R = sum of first row
n = sum of first column
A discussion and example are provided in the article, "Models and simulation for 2x2 contingency tables." In the article, I generate random tables, but it is straightforward to modify the program to enumerate them. (You can extend this idea to RxC tables, but then Monte Carlo simulation is preferable to trying to enumerate all possibilities.)
- Mark as New
- Bookmark
- Subscribe
- Mute
- RSS Feed
- Permalink
- Report Inappropriate Content
Yes, this is a 2x2 table. Disease is a binary and I have a binary grouping variable.
- Mark as New
- Bookmark
- Subscribe
- Mute
- RSS Feed
- Permalink
- Report Inappropriate Content
So, in a data step loop, increment or decrement the counts by 1 in each cell, and you can program the Chi-Squared formula based on the number of counts in each cell, and compute the value of its CDF or PDF for each iteration in the loop.
Paige Miller
- Mark as New
- Bookmark
- Subscribe
- Mute
- RSS Feed
- Permalink
- Report Inappropriate Content
- Mark as New
- Bookmark
- Subscribe
- Mute
- RSS Feed
- Permalink
- Report Inappropriate Content
You can implement the method in the DATA step with a 4-element array. You just have to decide on a convention for storing the elements of a 2x2 table into the array.
- Mark as New
- Bookmark
- Subscribe
- Mute
- RSS Feed
- Permalink
- Report Inappropriate Content
Sample size?
Proportion that is significant?
No clue without an idea of where you started. Something that doesn't show up as significant for a proportion at a sample size of 20 may well when the sample gets to 20,000.
- Mark as New
- Bookmark
- Subscribe
- Mute
- RSS Feed
- Permalink
- Report Inappropriate Content
I am trying to find an efficient way given just this information that I can calculate how many non-events would need to become events to make the pvalue significant using a two-tailed Fisher's exact test. My datalines are below for the 2 studies I am looking at. Datalines will likely be how I have to create a data set to start, so, if possible, a starting point like my datalines would be helpful. Thank you
data dataset;
input study $ num1 denom1 num2 denom2 pvalue;
datalines ;
A 14 33 8 37 0.071
B 10 33 5 37 0.143
;
run;- Mark as New
- Bookmark
- Subscribe
- Mute
- RSS Feed
- Permalink
- Report Inappropriate Content
Is the first p=value supposed to by 0.0751?
To make sure I understand:
- The first line is for Study A. That study has two groups.
For Group 1, there were 14 events out 33 subjects (so 19 nonevents). For Group 2, there were 8 events out of 37 subjects (so 29 nonevents)
- The second line is for Study B. For Group 1, there were 10 events out 33 subjects (so 23 nonevents). For Group 2, there were 5 events out of 37 subjects (so 32 nonevents)
In general, there is not a unique answer to your question. Many pairs of events will lead to statistically significant results. For example, when there are 0 events in Group1 and 22 events in Group2, that will be significant. Also, when there are 22 events in Group1 and 0 events in Group2.
Here's one way to use the DATA step to loop over all possible 2x2 tables that have the observed row sum and column sum. Then call PROC FREQ on each table. You can use additional logic to get the answer you want, after you define which of the many tables you want to choose. For now, I will just plot the p-values versus the number of events for Group 1. (You could use the number of non-events, if you prefer.)
/* for each study, numerate over the (1,1) Cell */
data dataset;
input study $ num1 denom1 num2 denom2 pvalue;
N = denom1 + denom2;
sumEvents = num1 + num2;
do x = 0 to SumEvents;
/* write a 2x2 table for PROC FREQ to analyze */
Group=1; Event=1; Count=x; output;
Group=1; Event=0; Count=denom1-x; output;
Group=2; Event=1; Count=SumEvents-x; output;
Group=2; Event=0; Count=denom2-SumEvents+x; output;
end;
datalines ;
A 14 33 8 37 0.0751
B 10 33 5 37 0.143
;
/* run PROC FREQ on all tables and get the two-sided p-values */
ods select none;
proc freq data=dataset;
by study x;
tables Event*Group / norow nocol nopercent;
exact fisher;
weight Count;
ods output FishersExact=FisherOut(where=(Name1='XP2_FISH'));
run;
ods select all;
/* perform an additional analysis to display the values you are looking for.
here, I simply plot the results so you can see the p-values as a function
of the number of successes in Group 1 */
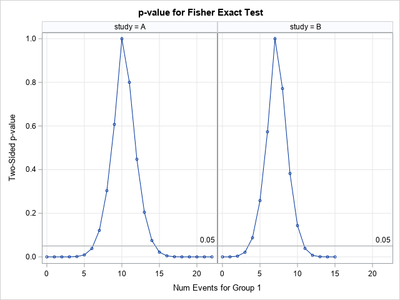
title "p-value for Fisher Exact Test";
proc sgpanel data=FisherOut;
panelby study;
series x=x y=nValue1 / markers;
refline 0.05 / axis=y label='0.05';
colaxis grid label="Num Events for Group 1";
rowaxis grid label="Two-Sided p-value";
run;
In Study A, the Exact Test is significant if the number of events is 6 or less, or 15 or more.
In Study B, the Exact Test is significant if the number of events is 3 or less, or 11 or more.
- Mark as New
- Bookmark
- Subscribe
- Mute
- RSS Feed
- Permalink
- Report Inappropriate Content
Rick,
You understand the setup of my datalines correctly.
The idea is to find the minimum number of events that need to change in order to reverse the pvalue from >0.05 to <0.05.
It looks like the code you provided shows that. Is it possible, instead of on a graph, to show a table of the changes? Something like below:
# of events changed Pvalue(hypothetical)
1 0.061
2 0.053
3 0.047
- Mark as New
- Bookmark
- Subscribe
- Mute
- RSS Feed
- Permalink
- Report Inappropriate Content
Sure. Only output the records where the pValue <= 0.05 that are in the left tail:
/* find the largest number of events in the left tail for which
the p-value is less than 0.05. If desired, add "# events changed" column */
data SolnLeftTail;
set FisherOut(rename=(nValue1=pValue));
by Study;
retain foundMax;
if first.study then do;
maxLeftEvents = .;
foundMax = 0;
end;
if NOT foundMax then do;
if pValue <= 0.05 then do;
maxLeftEvents = x;
output;
end;
else
foundMax = 1;
end;
run;
proc print data=SolnLeftTail;
var Study x pValue;
run;in the left tail of each study. I'll let you figure out the "# of events changed" column:
- Mark as New
- Bookmark
- Subscribe
- Mute
- RSS Feed
- Permalink
- Report Inappropriate Content
Rick,
If I could get more help. Attached is my code. I have applied the code as you laid out, but I am not able to replicate previous numbers that I have calculating the RFI. I have studies A-D with the numerator and denominator in my datalines. I know from previous research that the RFI for each study is 5, 5, 10 and 4. I am trying to reproduce the same code so that I can use SAS moving forward for these calculations. Again, the goal is to see the minimum number of nonevents that need to change to an event for each outcome measure in order for the nonsignificant p-value, as measured by Fisher's exact test, to become significant. Alpha level 0.05. Any help is greatly appreciated. Thank you
data rfi;
input study $ num1 denom1 num2 denom2;
N = denom1 + denom2;
sumEvents = num1 + num2;
do x = 0 to SumEvents;
/* write a 2x2 table for PROC FREQ to analyze */
Group=1; Event=1; Count=x; output;
Group=1; Event=0; Count=denom1-x; output;
Group=2; Event=1; Count=SumEvents-x; output;
Group=2; Event=0; Count=denom2-SumEvents+x; output;
end;
datalines;
A 3 151 3 149
B 3 151 2 149
C 5 125 2 50
D 3 57 2 60
;
run;
ods select none;
proc freq data=rfi;
by study x;
tables Event*Group / norow nocol nopercent;
exact fisher;
weight Count;
ods output FishersExact=FisherOut(where=(Name1='XP2_FISH'));
run;
ods select all;
proc sgpanel data=FisherOut;
panelby study;
series x=x y=nValue1 / markers;
refline 0.05 / axis=y label='0.05';
colaxis grid values=(0 1 2 3 4 5 6 7 8 9 10) label="Num Events for Group 1";
rowaxis grid label="Two-Sided p-value";
run;
data SolnLeftTail;
set FisherOut(rename=(nValue1=pValue));
by Study;
retain foundMax;
if first.study then do;
maxLeftEvents = .;
foundMax = 0;
end;
if NOT foundMax then do;
if pValue <= 0.05 then do;
maxLeftEvents = x;
output;
end;
else
foundMax = 1;
end;
run;
proc print data=SolnLeftTail;
var Study x pValue;
run;
*RFI- Study A - 5
Study B - 5
Study C - 10
Study D - 4;
Learn how use the CAT functions in SAS to join values from multiple variables into a single value.
Find more tutorials on the SAS Users YouTube channel.
SAS Training: Just a Click Away
Ready to level-up your skills? Choose your own adventure.