Interval estimation for binomial proportion: Wilson interval

[bigban777]

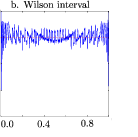
I need code for coverage probability (Wilson interval) to get following graph

thank you

P.S.

i found macro, but it didnt work for me.

Calculating the coverage probability for a given N and binomial p can be done in a single data step, summing the probability-weighted coverage indicators over the realized values of the random variate. Once this machinery is developed, we can call it repeatedly, using a macro, to find the results for different binomial p. We comment on the code internally.

%macro onep(n=,p=,alpha=.05);
data onep;
n = &n;
p = &p;
alpha = α
/* set up collectors of the weighted coverage indicators */
expcontrib_t = 0;
expcontrib_p4 = 0;
expcontrib_s = 0;
expcontrib_cp = 0;
/* loop through the possible observed successes x*/
do x = 0 to n;
  probobs = pdf('BINOM',x,p,n);  /* probability X=x */
  phat = x/n;
  zquant = quantile('NORMAl', 1 - alpha/2, 0, 1);
  p4 = (x+2)/(n + 4);

  /* calculate the half-width of the t and plus4 intervals */
  thalf = quantile('T', 1 - alpha/2,(n-1)) * sqrt(phat*(1-phat)/n);
  p4half = zquant * sqrt(p4*(1-p4)/(n+4));

  /* the score CI in R uses a Yates correction by default, and is 
     reproduced here */
  yates = min(0.5, abs(x - (n*p)));
  z22n = (zquant**2)/(2*n);
  yl = phat-yates/n;
  yu = phat+yates/n;
  slower = (yl + z22n - zquant * sqrt( (yl*(1-yl)/n) + z22n / (2*n) )) /
    (1 + 2 * z22n); 
  supper = (yu + z22n + zquant * sqrt( (yu*(1-yu)/n) + z22n / (2*n) )) /
    (1 + 2 * z22n); 

  /* cover = 1 if in the CI, 0 else */
  cover_t = ((phat - thalf) < p) and ((phat + thalf) > p);
  cover_p4 = ((p4 - p4half) < p) and ((p4 + p4half) > p);
  cover_s = (slower < p) and (supper > p);
  /* the Clopper-Pearson interval can be easily calculated on the fly */ 
  cover_cp = (quantile('BETA', alpha/2 ,x,n-x+1) < p) and 
    (quantile('BETA', 1 - alpha/2 ,x+1,n-x) > p); 

  /* cumulate the weighted probabilities */
  expcontrib_t = expcontrib_t + probobs * cover_t;
  expcontrib_p4 = expcontrib_p4 + probobs * cover_p4;
  expcontrib_s = expcontrib_s + probobs * cover_s;
  expcontrib_cp = expcontrib_cp + probobs * cover_cp;
  /* only save the last interation */
  if x = N then output;
  end;
run;
%mend onep;

The following macro calls the first one for a series of binomial p for a fixed N. Since the macro %do loop can only iterate through integers, we have to do a little division; the %sysevelf function will do this within the macro.

%macro repcicov(n=, lop=, hip=, byp=, alpha= .05);
/* need an empty data set to store the results */
data summ; set _null_; run;
%do stepp = %sysevalf(&lop / &byp, floor) %to %sysevalf(&hip / &byp,floor);
  /* note that the p sent to the %onep macro is a 
                           text string like "49 * .001" */
  %onep(n = &n, p = &stepp * &byp, alpha = &alpha);
  /* tack on the current results to the ones finished so far */
  /* this is a simple but inefficient way to add each binomial p into 
     the output data set */
  data summ; set summ onep; run;
%end;
%mend repcicov;

/* same parameters as in R */
%repcicov(n=50, lop = .01, hip = .3, byp = .001);

Finally, we can plot the results. One option shown here and not mentioned in the book are the mode=include option to the symbol statement, which allows the two distinct pieces of the T coverage to display correctly.

goptions reset=all;
legend1 label=none position=(bottom right inside)
        mode=share across=1 frame value = (h=2);
axis1 order = (0.85 to 1 by 0.05) minor=none 
   label = (a=90 h=2 "Coverage probability") value=(h=2);
axis2 order = (0 to 0.3 by 0.05) minor=none 
   label = (h=2 "True binomial p") value=(h=2);
symbol1 i = j v = none l =1 w=3 c=blue mode=include;
symbol2 i = j v = none l =1 w=3 c=red;
symbol3 i = j v = none l =1 w=3 c=lightgreen;
symbol4 i = j v = none l =1 w=3 c=black;
proc gplot data = summ;
plot (expcontrib_t expcontrib_p4  expcontrib_s  expcontrib_cp) * p 
  / overlay legend vaxis = axis1 haxis = axis2 vref = 0.95 legend = legend1;
label expcontrib_t = "T approximation" expcontrib_p4 = "P4 method"
      expcontrib_s = "Score method" expcontrib_cp = "Exact (CP)";
run; quit;

[FreelanceReinh · Accepted solution]

Hello @bigban777,

I haven't checked all the details of the code you posted, but after the following corrections/modifications, the graphs are produced and look plausible:

1. Line 5 must read: alpha = α
2. The calculation of cover_cp fails in the degenerate cases x=0 and x=n, so these cases need to be handled separately:
   

   if 0<x<n then
       cover_cp = (quantile('BETA', alpha/2 ,x,n-x+1) < p) and 
                  (quantile('BETA', 1 - alpha/2 ,x+1,n-x) > p);
     else if x=0 then
       cover_cp = (0 < p) and (quantile('BETA', 1 - alpha/2 ,x+1,n-x) > p);
     else if x=n then
       cover_cp = (quantile('BETA', alpha/2 ,x,n-x+1) < p) and (1 > p);

3. Of course, the parameters in the call of macro REPCICOV have to be adjusted to the n and p range you want. The latter appears to be the interval [0, 1] in your graph. So, you could use
   

   %repcicov(n=50, lop = 0, hip = 1, byp = .001);

   (Please choose the value of n yourself.)
4. The x axis range needs to be adapted accordingly:
   

   axis2 order = (0 to 1 by 0.05) minor=none

5. If you want to see the graph for the Wilson interval alone, you can delete the other three plot requests or comment them out:
   

   plot (/* expcontrib_t expcontrib_p4 */ expcontrib_s /* expcontrib_cp */) * p 

[bigban777]

Hi,

i did change in my code as you said but it doesnt show graph. Here is my fixes code. Where is mistake?

%macro onep(n=,p=,alpha=.05);
data onep;
n = &n;
p = &p;
alpha = α
/* set up collectors of the weighted coverage indicators */
expcontrib_t = 0;
expcontrib_p4 = 0;
expcontrib_s = 0;
expcontrib_cp = 0;
/* loop through the possible observed successes x*/
do x = 0 to n;
  probobs = pdf('BINOM',x,p,n);  /* probability X=x */
  phat = x/n;
  zquant = quantile('NORMAl', 1 - alpha/2, 0, 1);
  p4 = (x+2)/(n + 4);

  /* calculate the half-width of the t and plus4 intervals */
  thalf = quantile('T', 1 - alpha/2,(n-1)) * sqrt(phat*(1-phat)/n);
  p4half = zquant * sqrt(p4*(1-p4)/(n+4));

  /* the score CI in R uses a Yates correction by default, and is 
     reproduced here */
  yates = min(0.5, abs(x - (n*p)));
  z22n = (zquant**2)/(2*n);
  yl = phat-yates/n;
  yu = phat+yates/n;
  slower = (yl + z22n - zquant * sqrt( (yl*(1-yl)/n) + z22n / (2*n) )) /
    (1 + 2 * z22n); 
  supper = (yu + z22n + zquant * sqrt( (yu*(1-yu)/n) + z22n / (2*n) )) /
    (1 + 2 * z22n); 

  /* cover = 1 if in the CI, 0 else */
  cover_t = ((phat - thalf) < p) and ((phat + thalf) > p);
  cover_p4 = ((p4 - p4half) < p) and ((p4 + p4half) > p);
  cover_s = (slower < p) and (supper > p);
  /* the Clopper-Pearson interval can be easily calculated on the fly */ 
  cover_cp = (quantile('BETA', alpha/2 ,x,n-x+1) < p) and 
    (quantile('BETA', 1 - alpha/2 ,x+1,n-x) > p); 
	
	if 0<x<n then
    cover_cp = (quantile('BETA', alpha/2 ,x,n-x+1) < p) and 
               (quantile('BETA', 1 - alpha/2 ,x+1,n-x) > p);
  else if x=0 then
    cover_cp = (0 < p) and (quantile('BETA', 1 - alpha/2 ,x+1,n-x) > p);
  else if x=n then
    cover_cp = (quantile('BETA', alpha/2 ,x,n-x+1) < p) and (1 > p);
  
  /* cumulate the weighted probabilities */
  expcontrib_t = expcontrib_t + probobs * cover_t;
  expcontrib_p4 = expcontrib_p4 + probobs * cover_p4;
  expcontrib_s = expcontrib_s + probobs * cover_s;
  expcontrib_cp = expcontrib_cp + probobs * cover_cp;
  /* only save the last interation */
  if x = N then output;
  end;
run;
%mend onep;


%macro repcicov(n=, lop=, hip=, byp=, alpha= .05);
/* need an empty data set to store the results */
data summ; set _null_; run;
%do stepp = %sysevalf(&lop / &byp, floor) %to %sysevalf(&hip / &byp,floor);
  /* note that the p sent to the %onep macro is a 
                           text string like "49 * .001" */
  %onep(n = &n, p = &stepp * &byp, alpha = &alpha);
  /* tack on the current results to the ones finished so far */
  /* this is a simple but inefficient way to add each binomial p into 
     the output data set */
  data summ; set summ onep; run;
%end;
%mend repcicov;

/* same parameters as in R */
%repcicov(n=50, lop = 0, hip = 1, byp = .001);

goptions reset=all;
legend1 label=none position=(bottom right inside)
        mode=share across=1 frame value = (h=2);
axis1 order = (0.85 to 1 by 0.05) minor=none 
   label = (a=90 h=2 "Coverage probability") value=(h=2);
axis2 order = (0 to 0.3 by 0.05) minor=none 
   label = (h=2 "True binomial p") value=(h=2);
symbol1 i = j v = none l =1 w=3 c=blue mode=include;
symbol2 i = j v = none l =1 w=3 c=red;
symbol3 i = j v = none l =1 w=3 c=lightgreen;
symbol4 i = j v = none l =1 w=3 c=black;
proc gplot data = summ;
plot (/*expcontrib_t expcontrib_p4 */ expcontrib_s  /*expcontrib_cp*/) * p 
  / overlay legend vaxis = axis1 haxis = axis2 vref = 0.95 legend = legend1;
label expcontrib_t = "T approximation" expcontrib_p4 = "P4 method"
      expcontrib_s = "Score method" expcontrib_cp = "Exact (CP)";
run; quit;

Thank you

[FreelanceReinh]

---

@bigban777 wrote:

Hi,

i did change in my code as you said

---

Well, you did, but neither correctly, nor completely.

• The new definition of cover_cp should have replaced the old one. So, just delete the two lines of code after the comment
  "/* the Clopper-Pearson interval ...".
• You forgot to implement item 4: axis2 order = (0 to 1 by 0.05) minor=none
  Please note that this axis definition is to replace the old axis2 statement.

But even without these corrections your code produces a (partial) graph in my SAS session. Maybe you have to double-click the item representing the plot in the results window?

[Edit 2019-04-30: Reattached screenshot, which had been deleted by mistake.]

[bigban777]

for some reason i couldnt get result. I use SAS on Demand.

Could you post graph what you got please.

[FreelanceReinh]

I am sorry, but I think this might violate the terms of my SAS license agreement.

I'm not familiar with SAS on Demand. Are you unable to create any graph with that software?

If so, I suggest you post this general problem in a new thread, e.g., in the "SAS/GRAPH and ODS Graphics" subforum.

[data_null__]

Is this the same thing PROC FREQ can do?

http://support.sas.com/documentation/cdl/en/statug/68162/HTML/default/viewer.htm#statug_freq_details...

[FreelanceReinh]

@data_null__: Yes, I assume it's the same CI (but haven't checked). However, I guess it would not help much to replace the data step formula in the OP's macro by one or more PROC FREQ calls.

[data_null__]

---

@FreelanceReinhard wrote:

@data_null__: Yes, I assume it's the same CI (but haven't checked). However, I guess it would not help much to replace the data step formula in the OP's macro by one or more PROC FREQ calls.

---

I'm not suggesting that you loop on PROC FREQ I was asking if the entire thing can be done with PROC FREQ.

It might be that looping on PROC FREQ is better than "this" program.

[FreelanceReinh]

---

@data_null__ wrote:

... I was asking if the entire thing can be done with PROC FREQ.

I don't think so. PROC FREQ offers a variety of plots, but the type of graph produced by the OP's program is not among these, I think. Plotting coverage probabilities is rather something for researchers in mathematical statistics than for the target audience of PROC FREQ, i.e. users who are analyzing data.