- Home
- /
- Programming
- /
- Programming
- /
- Re: If statement Short circuiting and Lag function
- RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
- Mark as New
- Bookmark
- Subscribe
- Mute
- RSS Feed
- Permalink
- Report Inappropriate Content
Hi All,
I am trying to understand the Output from the below piece of SAS Code . This Code is actually a simplified version to the one posted by @ChrisHemedinger in his blog back in 2012 :https://blogs.sas.com/content/sasdummy/2012/01/03/pitfalls-of-the-lag-function/
Here is the Code :
data test;
infile datalines dlm=',' dsd;
input a b;
datalines;
4272451,17878
4272451,17878
run;
data testLags;
retain e 1;
set test;
if a=lag(a) and b>lag(b) then
e=e+1;
else if a^=lag(a) or lag(a)=. then
e=1;
run;
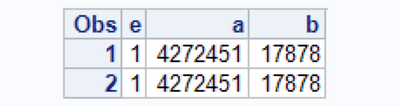
proc print data=testLags;
run;The above gives the following output :
This is known as "Short circuiting" of the Boolean expression as i understand it .
So basically during the first iteration of the above Data step , the second condition : b > lag(b) in the IF Statement is never processed since first condition in the IF statement ie a = lag(a) resolves to FALSE. This would mean in the second iteration the IF statement should evaluate as below :
If 4272451 = 4272451 AND 17878 > . , which should evaluate to TRUE and so the variable e should be incremented by 1 and become 2 in the second observation. Note the lag(b) in the second iteration should resolve to a missing value represented by a . ( period ) because this is the first time that lag(b) is getting processed in the Data Step .
So what is going on here ? Am i missing something ? Why isn't e=2 in the second observation?
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- RSS Feed
- Permalink
- Report Inappropriate Content
Hi again,
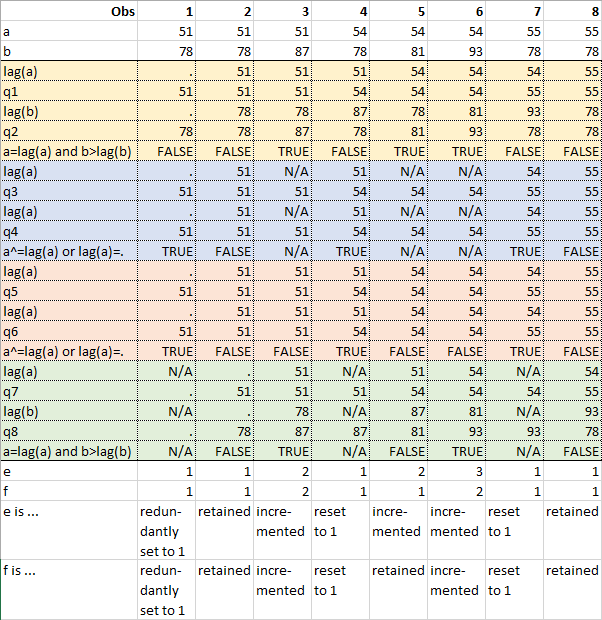
Now I have put my notes in tabular form, as shown below.
To save horizontal space, I've transposed the table. So, observations are aligned in columns and the input data are entered in rows "a" and "b". Please note that I have shed variable C as well as all but the last two digits of A and B in order to reduce redundancy and clutter. (This is where the "54", "51" etc. in my previous post came from.)
Based on my assumption that each occurrence of the LAG function in a data step has its own queue, there are eight rows containing LAG function values (lag(a), lag(b)), each of which is followed by a row for the (invisible) value contained in the associated queue (q1, q2, etc.). They occur in the same order as in the data step.
The "lag(a)" or "lag(b)" terms in the four Boolean expressions correspond to the rows of the same headers and with the same background color. "N/A" is entered if an ELSE clause is not executed for logical reasons. Obviously, rows "e" and "f" contain the results, followed by verbal descriptions of what (I think) happened.
This is a screenshot of an Excel table. Virtually all cells were computed using Excel formulas (which in turn implement my assumptions about the workings of this data step). So, I can enter new data in rows "a" and "b" and let Excel calculate e and f. (I tested this with a few random permutations of the data.)
If someone is interested, I can upload the xlsx file, whose formulas use German function names, though.
I haven't read Chris' blog article in detail yet. In particular, I haven't checked if I was correct in disregarding short circuiting within Boolean expressions. However, at least for the current input data (and the few permutations I checked) the results match those obtained with SAS.
- Mark as New
- Bookmark
- Subscribe
- Mute
- RSS Feed
- Permalink
- Report Inappropriate Content
- Mark as New
- Bookmark
- Subscribe
- Mute
- RSS Feed
- Permalink
- Report Inappropriate Content
That's what i thought initially . But if you look at the blog or my reply below , i cannot understand how to make sense of the value of variable f in the obervation 5 . why is it 1 instead 2 ?
- Mark as New
- Bookmark
- Subscribe
- Mute
- RSS Feed
- Permalink
- Report Inappropriate Content
I just walked through this data step manually and applied my understanding of the LAG function (essentially based on practical experience) -- and was happy to see that the result matches the actual output dataset. According to my notes, the IF condition which would need to be met in order to trigger the incrementation of F in the 5th observation reads "if 54=51 and 81>87" -- i.e., not even one of the two expressions is true, hence no incrementation occurs and F remains 1.
I think, key points are:
- Each occurrence of the LAG function in a data step has its separate queue.
- ELSE clauses (and in particular LAG functions contained therein) are not executed if the preceding IF condition was met.
- I did not assume any short-circuiting within a Boolean expression (although I know that it occurs under certain other circumstances).
(I may be wrong, this is just based on my experience 1997 - 2018.)
Perhaps I can think about and elaborate on this a little more tomorrow (it's close to midnight in my time zone).
- Mark as New
- Bookmark
- Subscribe
- Mute
- RSS Feed
- Permalink
- Report Inappropriate Content
Hi again,
Now I have put my notes in tabular form, as shown below.
To save horizontal space, I've transposed the table. So, observations are aligned in columns and the input data are entered in rows "a" and "b". Please note that I have shed variable C as well as all but the last two digits of A and B in order to reduce redundancy and clutter. (This is where the "54", "51" etc. in my previous post came from.)
Based on my assumption that each occurrence of the LAG function in a data step has its own queue, there are eight rows containing LAG function values (lag(a), lag(b)), each of which is followed by a row for the (invisible) value contained in the associated queue (q1, q2, etc.). They occur in the same order as in the data step.
The "lag(a)" or "lag(b)" terms in the four Boolean expressions correspond to the rows of the same headers and with the same background color. "N/A" is entered if an ELSE clause is not executed for logical reasons. Obviously, rows "e" and "f" contain the results, followed by verbal descriptions of what (I think) happened.
This is a screenshot of an Excel table. Virtually all cells were computed using Excel formulas (which in turn implement my assumptions about the workings of this data step). So, I can enter new data in rows "a" and "b" and let Excel calculate e and f. (I tested this with a few random permutations of the data.)
If someone is interested, I can upload the xlsx file, whose formulas use German function names, though.
I haven't read Chris' blog article in detail yet. In particular, I haven't checked if I was correct in disregarding short circuiting within Boolean expressions. However, at least for the current input data (and the few permutations I checked) the results match those obtained with SAS.
- Mark as New
- Bookmark
- Subscribe
- Mute
- RSS Feed
- Permalink
- Report Inappropriate Content
Wow, thanks for the detailed treatment @FreelanceReinh!
My blog does cite the practice of Boolean short-circuiting, which would allow the language processor to discontinue evaluating a Boolean expression as soon as one part of it evaluated to False (or 0). However, I can't say for certain under which conditions SAS employs this practice. It's well-defined in other compiled programming languages like C, and experienced programmers may be tempted to rely on it. However, I think it's a good practice to be more explicit about the conditions in your SAS program for readability sake as well as for a more deterministic approach.
- Mark as New
- Bookmark
- Subscribe
- Mute
- RSS Feed
- Permalink
- Report Inappropriate Content
Thanks, @FreelanceReinh
It helps to see it all listed out here.
The key part that I missed:
On the 5th observation, each instance of lag(b) has its own queue. When computing F, lag(b) is 87, not 78. On the 4th observation, this particular lag(b) did not execute, so when it executes on the 5th observation it is picking up B from observation #3.
- Mark as New
- Bookmark
- Subscribe
- Mute
- RSS Feed
- Permalink
- Report Inappropriate Content
@FreelanceReinh Thank you for your detailed explanation of the behavior various Lag functions in this Data Step. This has been a good discussion. I initially thought this was some kind of a Bug with the Lag function behaving weirdly as in case of the 5th observation. But your detailed analysis of each lag function occurrence having its own queue makes a lot of sense to explain this and demonstrate that is in fact not a Bug but it is working as designed. As mentioned in Chris's Blog, the best way to avoid this kind of behavior is to declare 2 variables for lag(a) and lag(b) respectively before the IF statements and then use these variables in the conditions of the If statements. This ensures lag(a) and lag(b) are each processed only once during each iteration of the Data Step.
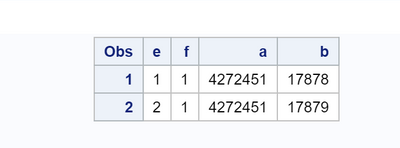
The Data Step example can further be simplified as below to show the same kind of behavior, this time in only the second observation.
data test;
infile datalines dlm=',' dsd;
input a b;
datalines;
4272451,17878
4272451,17879
;
run;
data testLags;
retain e f ( 1 1);
set test;
if a=lag(a) and b>lag(b) then e=e+1; /**(1)**/
else if a^=lag(a) or lag(a)=. then e=1; /**(2)**/
if a^= lag(a) or lag(a)=. then f=1; /**(3)**/
else if a=lag(a) and b>lag(b) then f=f+1; /**(4)**/
run;
proc print;
run;
Output :
Thanks also to others who participated in this discussion.
- Mark as New
- Bookmark
- Subscribe
- Mute
- RSS Feed
- Permalink
- Report Inappropriate Content
@FreelanceReinh wrote:
I haven't read Chris' blog article in detail yet. In particular, I haven't checked if I was correct in disregarding short circuiting within Boolean expressions. However, at least for the current input data (and the few permutations I checked) the results match those obtained with SAS.
I've created a modified version of my Excel table, now implementing Boolean short-circuiting (for both "FALSE and X ==> FALSE" and "TRUE or X ==> TRUE"). Compared to the original table, 57 (!) cells have changed, including two values of E (obs. 5 and 6 have decreased by 1) and two values of F (obs. 3 and 6 have decreased by 1). Boolean short-circuiting for "FALSE and X ==> FALSE" alone changes two values of E and one of F.
Consequently, Boolean short-circuiting does not seem to occur in this specific SAS program. It is rather the fact that ELSE clauses are not executed if the preceding IF condition is true.
Meanwhile, the exact conditions under which Boolean short-circuiting occurs remain mysterious (to me; see examples under the spoiler).
data test;
a=0; b=0;
if b=1 & 1/a>0;
run; /* No note about "Division by zero ..." in the log, seemingly because b=1 is false. */
data test;
a=0;
if 0 & 1/a>0;
run; /* This time "Division by zero ..." message appears, although 0 is obviously false. */
- Mark as New
- Bookmark
- Subscribe
- Mute
- RSS Feed
- Permalink
- Report Inappropriate Content
+! for creative use of the spoiler feature 🙂
- Mark as New
- Bookmark
- Subscribe
- Mute
- RSS Feed
- Permalink
- Report Inappropriate Content
- Mark as New
- Bookmark
- Subscribe
- Mute
- RSS Feed
- Permalink
- Report Inappropriate Content
Great use case for the DATA step debugger in SAS Enterprise Guide. In this case, the second OBS does not trigger either condition (the IF or the ELSE IF), so the value of e remains at 1.
- Mark as New
- Bookmark
- Subscribe
- Mute
- RSS Feed
- Permalink
- Report Inappropriate Content
I can't prove it, but based on your results the process must be this.
In the first statement, SAS evaluates both LAG functions first, then makes the comparisons as the second step. So LAG(B) does actually execute on the first statement. The comparison comparing b to lag(b) doesn't execute, but the lag function itself has already executed.
- Mark as New
- Bookmark
- Subscribe
- Mute
- RSS Feed
- Permalink
- Report Inappropriate Content
@Astounding and @ChrisHemedinger . Assuming your explanation is correct , how do i make sense of the discrepancy seen in the 5th observation from Chris's blog : https://blogs.sas.com/content/sasdummy/2012/01/03/pitfalls-of-the-lag-function/
Should'nt the value of variable f be 2 instead of 1 ?
data test;
infile datalines dlm=',' dsd;
input a b c;
datalines;
4272451,17878,17878
4272451,17878,17878
4272451,17887,17887
4272454,17878,17878
4272454,17881,17881
4272454,17893,17893
4272455,17878,17878
4272455,17878,18200
run;
data testLags;
retain e f ( 1 1);
set test;
if a=lag(a) and b>lag(b) then
e=e+1;
else if a^=lag(a) or lag(a)=. then
e=1;
if a^=lag(a) or lag(a)=. then
f=1;
else if a=lag(a) and b>lag(b) then
f=f+1;
run;Output :
Obs e f a b c 1 1 1 4272451 17878 17878 2 1 1 4272451 17878 17878 3 2 2 4272451 17887 17887 4 1 1 4272454 17878 17878 5 2 1 4272454 17881 17881 6 3 2 4272454 17893 17893 7 1 1 4272455 17878 17878 8 1 1 4272455 17878 18200
- Mark as New
- Bookmark
- Subscribe
- Mute
- RSS Feed
- Permalink
- Report Inappropriate Content
I can't explain it. It's difficult to even come up with a valid test program under these conditions. The best I could do was to demonstrate that this condition is true: a ^= lag(a)
To do that, I substituted for this statement:
if a^=lag(a) or lag(a)=. then
f=1;
These are the statements that I replaced it with:
if (a^=lag(a)) * 0 or lag(a)=. then
f=1;
if a^=lag(a) or (lag(a)=.) * 0 then
f=1;
Learn how use the CAT functions in SAS to join values from multiple variables into a single value.
Find more tutorials on the SAS Users YouTube channel.
SAS Training: Just a Click Away
Ready to level-up your skills? Choose your own adventure.