Distinct powers of integer combinations

[teelov]

Hello Folks, I thought it was about time i used SAS for some complex maths problems, as most of the time my main use for SAS is data manipulation. lately i've had some really nice problems to solve and in particular, help me grasp complex maths. but this particular exercise has me stumped, and i believe its due to the limitation of how i use SAS.

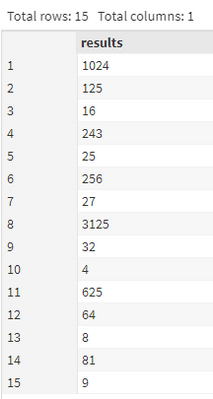
Consider all integer combinations of ab for 2 ≤ a ≤ 5 and 2 ≤ b ≤ 5:

22=4, 23=8, 24=16, 25=32
32=9, 33=27, 34=81, 35=243
42=16, 43=64, 44=256, 45=1024
52=25, 53=125, 54=625, 55=3125

If they are then placed in numerical order, with any repeats removed, we get the following sequence of 15 distinct terms: 4, 8, 9, 16, 25, 27, 32, 64, 81, 125, 243, 256, 625, 1024, 3125 How many distinct terms are in the sequence generated by ab for 2 ≤ a ≤ 100 and 2 ≤ b ≤ 100?

here is some sample code of how we are trying to solve the problem, the issue is, its taking 24hrs to run:

the issue could be that i'm not using multithreading as per datastep, so i considered casting the interger to an SQL box as we know SAS struggles with numbers beyond 15-16 characters.

from some early calculations the dataset will end up with around 9800 rows, so i'm not sure where the bottleneck is

%macro add_num (num1=,num2=);

%global ans;

%let len1 = %length(&num1);
%let len2 = %length(&num2);

%let maxlen = %sysfunc(max(&len1,&len2));

%if &maxlen ^= &len1 %then
  %let num1 = %sysfunc(repeat(0,%eval(&maxlen - &len1 - 1)))&num1;
%if &maxlen ^= &len2 %then
  %let num2 = %sysfunc(repeat(0,%eval(&maxlen - &len2 - 1)))&num2;

%let ten = 0;
%let ans = ;

%do i = &maxlen %to 1 %by -1;

  %let digit1 = %sysfunc(substr(&num1,&i,1));
  %let digit2 = %sysfunc(substr(&num2,&i,1));

  %let tmp = %eval(&digit1 + &digit2 + &ten);

  %if %length(&tmp) = 2 %then
  %do;
    %let unit = %sysfunc(substr(&tmp,2,1));
     %let ten = 1;
  %end;
  %else
  %do;
    %let unit = &tmp;
     %let ten = 0;    
  %end;

  %let ans = &unit&ans;

%end;

%if &ten = 1 %then 
  %let ans = &ten&ans;

/*%put Addition Complete : &num1 + &num2 = &ans;*/

%mend;

%macro multi_num(num1=,multi=);
%global ans;
%let num2 = &num1;
%let later = &num1;
%do j = 1 %to %eval(&multi - 1);
  %add_num(num1=&num1,num2=&num2);
  %let num1 = &ans;
%end;
/*%put Multiplication Complete : &num2 x &multi = &ans;*/
%mend;


%macro fact(factorial=);
%global ans;
%let ans = ;
%multi_num (num1=&factorial,multi=%eval(&factorial-1));
%do a=%eval(&factorial-2) %to 2 %by -1;
%multi_num (num1=&ans,multi=&a);
%end;

%put Factorial Complete : &factorial.! is &ans;
%mend;

%macro expo(base=,expo=);
%global ans;
%let ans = ;
%multi_num (num1=&base,multi=&base);
%do a=%eval(&expo-2) %to 1 %by -1;
%multi_num (num1=&ans,multi=&base);
%end;

%put Exponential Complete : &base. to the power of &expo. is &ans;
%mend;


%macro _29;

data results;
  length results $32767;

%do _first=2 %to 100;
  %let first_time= 1 ;
  %do _second=2 %to 100;

    %if &first_time = 1 %then
     %do;
      %multi_num (num1=&_first,multi=&_first);
       %let first_time=0;
     %end;
     %else
     %do;
      %multi_num (num1=&ans,multi=&_first);
     %end;
     results = "&ans.";
     output;

  %end;
%end;

run;

proc sort data = results nodupkey ;
  by results ;
run;

%let dsid=%sysfunc(open(results));
%let results=%sysfunc(attrn(&dsid,nlobs));
%let rc=%sysfunc(close(&dsid));

proc datasets lib=work nolist noprint;
  delete results;
run;quit;
  

%put Answer is: &results;

%mend;

%_29;

     

[RW9]

Sorry, am really not understanding that formula.  What I will however say is that usinig global macro variables, and doing all the processing in macro is not the way forward.  If you can explain the formula, i can provide code, but almost any imaginable formula should be doable in a simple datastep, not sure why you have multiple macro calls in loops etc.  Just generating vast amounts of code.  Simplify your code using Base SAS.

[teelov]

when you run the code for a small amount, lets say 20 - then in the log you can see what my macro is doing

Addition Complete : 4 + 4 = 8

Addition Complete : 8 + 4 = 12

Addition Complete : 12 + 04 = 16

Multiplication Complete : 4 x 4 = 16

Addition Complete : 16 + 16 = 32

Addition Complete : 32 + 16 = 48

Addition Complete : 48 + 16 = 64

Multiplication Complete : 16 x 4 = 64

Addition Complete : 64 + 64 = 128

Addition Complete : 128 + 064 = 192

Addition Complete : 192 + 064 = 256

Multiplication Complete : 64 x 4 = 256

Addition Complete : 256 + 256 = 512

Addition Complete : 512 + 256 = 768

Addition Complete : 768 + 256 = 1024

Multiplication Complete : 256 x 4 = 1024

put in a list, without checking whether they have already been obtained for the first time, all the terms that can be generated by \ (a ^ b \) by varying a and b from 2 to 100,remove all duplicates from this list,look at the number of term it stays in our list.

i know this way is not optimal

for the bigger numbers we'd expect something like this

Multiplication Complete : 239072435685151324847153 x 17 = 4064231406647572522401601

after some research someone has done the following in python

  powers = []
 for a in range (2, 101):
     for b in range (2, 101):
         powers.append (a ** b)
 #Suppresion of all duplicates in the powers list
 result = len (list (set (powers)))
 print (result) 

[ChrisBrooks]

Along with @RW9 I don't really understand what you're trying to do here but I agree that macro isn't the way forward - if you can explain it more simply (ideally step by step for a couple of values) we can almost certainly supply code. For example for this sort of computationally expensive calculation I'm thinking that storing the output initially in a hash object should be faster and would remove the need to de-duplicate at the end.

[Astounding]

First, let me give you a simple SAS program that (I think) handles your original case:

data combinations;

do a=2 to 5;

   do b=2 to 5;

      result = a**b;

      output;

   end;

end;

run;

That gives you all the combinations.  Perhaps you are looking to subset that to get unique values for RESULT.  We know there will be duplicates, since 2**4 = 4**2.  Finding unique values is fairly easy, so we can skip that here.

When you get to the higher ranges you are talking about, as you noted you are going beyond SAS's capacity to store integers accurately.  You would have to revise the RESULT calculations to actually store the result in a different format.  For example, you might break down A and B into prime components and store the results as the combined powers for each prime component.  That's so wordy, I couldn't understand it if I read it.  So here is an example.

a = 15, b = 36

Instead of storing 15**36, break down each component.

A:  components are 3 and 5, each raised to the first power.

B:  components are 2 and 3, each raised to the second power.

So you could have variables in your data set representing this:

a_2 = 0, a_3 = 1, a_5 = 1

Since 36 = (2**2) * (3**2):

b_2 = 2, b_3 = 2, b_5 = 0

You just need to factor each number down to the powers of its prime component.

Since there are a limited number of prime numbers between 2 and 100, there are a limited number of variables to compute, with a reasonable range to their values.

Then you need to compute the similar results for a**b.  I would need 2 cups of coffee before attempting that, but the idea is that:

result_2 = powers of 2 represented within a**b

result_3 = powers of 3 represented within a**b

result_5 = powers of 5 represented with a**b

[teelov]

You have explained it a lot better than i could, so thanks for that.

the example at the top is using a max power of 5

which i think the code works for, so really its about my not using SAS correctly, or to my limitations of algorithms to get to the 100.

here are the results.

Multiplication Complete : 2 x 2 = 4

Multiplication Complete : 4 x 2 = 8

Multiplication Complete : 8 x 2 = 16

Multiplication Complete : 16 x 2 = 32

Multiplication Complete : 3 x 3 = 9

Multiplication Complete : 9 x 3 = 27

Multiplication Complete : 27 x 3 = 81

Multiplication Complete : 81 x 3 = 243

Multiplication Complete : 4 x 4 = 16

Multiplication Complete : 16 x 4 = 64

Multiplication Complete : 64 x 4 = 256

Multiplication Complete : 256 x 4 = 1024

Multiplication Complete : 5 x 5 = 25

Multiplication Complete : 25 x 5 = 125

Multiplication Complete : 125 x 5 = 625

Multiplication Complete : 625 x 5 = 3125

[Rick_SAS]

Here's a hint: These sort of "math challenge" problems are usually constructed so that a brute force computation will require a long time or will be numerically infeasible. The key is usually to use mathematical ideas to reduce the complexity of the computations so that it is solvable quickly.

For this problem, I think you should use the prime factorization theorem which states that each positive number can be expressed UNIQUELY as the product of prime factors (up to the ordering of the factors).  If I were to solve this problem, I would NEVER FORM any of the powers a**b, since that will overflow. Instead, I would represent each number in the range [2,100] by its unique ordered prime factorization. (There are only 25 primes less than 100: {2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97}.)   

You can then use programmig and bookkeeping to count the number of distinct value of a**b. I'll leave that effort to others.

[teelov]

Thank you, this makes sense and gives me something to go on..

i will leave the post open for now as i could hit a few snags.

[Ksharp]

How about this one ?

data z;
do a=2 to 100;
 do b=2 to 100;
   value=b*log(a);output;
 end;
end;
run;

proc sql;
select count(distinct value) as n
 from z;
quit;

SAS Output

n
9240