- Home
- /
- Programming
- /
- Programming
- /
- Re: Code to perform simulation
- RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
- Mark as New
- Bookmark
- Subscribe
- Mute
- RSS Feed
- Permalink
- Report Inappropriate Content
Hello,
I've a data set of 70 cases, and I have an equation involving 17 variables from the data that I'd like to test on. Specifically I'd like to test if changing +/-5% magnitude of each variable ^one at a time^, what would the variation for the Y value on the left of the equation and which variable would produce the largest variation.
Here is the hypothetical data of 10 cases.
data have; input
ID A B C D E N1 N2 N3 N4 N5 N6 D1 D2 D3 D4 D5 D6;
datalines;
1 100 10 0.5 15 10 35 8 6 4 2 1 39 8 5 5 1 2
2 200 11 0.3 25 15 35 8 6 4 2 2 42 7 7 4 2 3
3 300 20 0.4 15 14 40 8 6 4 2 3 53 9 6 5 3 2
4 150 19 0.1 5 19 27 8 6 4 2 4 35 4 9 7 4 4
5 400 40 0.5 35 20 50 8 6 4 2 6 79 17 4 9 1 5
6 900 50 0.4 55 15 70 8 6 4 2 9 85 5 9 4 2 11
7 600 30 -0.5 20 29 60 8 6 4 2 2 62 16 7 5 4 10
8 500 30 0.2 25 17 50 8 6 4 2 3 60 4 9 8 2 5
9 400 30 0.4 19 16 44 8 6 4 2 1 49 8 4 4 5 9
10 700 45 0.3 39 14 34 8 6 4 2 1 38 3 2 5 4 12
;
run;
data want; set have;
Numerator=N1-N2-N3-N4-N5-N6;
Denominator=D1-D2-D3-D4-D5-D6;
Wgt=Numerator/Denominator;
if Wgt >1 then Wgt=1;
Y=(A*B*(1+C)- D - E)*Wgt;
run;
proc print noobs; run;
I was told I should just sample 5 case at a time for the work as the running time is intensive. If I do, my question is how do write a SAS code to tell SAS to add +5% to one data element a time - so it would be first do A*1.05, calculate Y value for the 5 cases, then get average and standard deviation, then reset to do B*1.05, calculate Y value and so on. When it's all done for all 17 variables, do -0.5% magnitude. How do I even start to write the macro, or if SAS has ready to use procedure for this kind of simulation work?
Many thanks
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- RSS Feed
- Permalink
- Report Inappropriate Content
"What I should have asked is once I get Y values under different scenarios of changes, I'll calculate the proportion or share - Y1/sum of Y1-10, Y2/sum of Y, etc.) and get mean and SD of the share."
Post your output and formula would better to clarify your question.
This code is almost the same as above .
data have; input
ID A B C D E N1 N2 N3 N4 N5 N6 D1 D2 D3 D4 D5 D6;
datalines;
1 100 10 0.5 15 10 35 8 6 4 2 1 39 8 5 5 1 2
2 200 11 0.3 25 15 35 8 6 4 2 2 42 7 7 4 2 3
3 300 20 0.4 15 14 40 8 6 4 2 3 53 9 6 5 3 2
4 150 19 0.1 5 19 27 8 6 4 2 4 35 4 9 7 4 4
5 400 40 0.5 35 20 50 8 6 4 2 6 79 17 4 9 1 5
6 900 50 0.4 55 15 70 8 6 4 2 9 85 5 9 4 2 11
7 600 30 -0.5 20 29 60 8 6 4 2 2 62 16 7 5 4 10
8 500 30 0.2 25 17 50 8 6 4 2 3 60 4 9 8 2 5
9 400 30 0.4 19 16 44 8 6 4 2 1 49 8 4 4 5 9
10 700 45 0.3 39 14 34 8 6 4 2 1 38 3 2 5 4 12
;
run;
proc iml;
use have(keep= A B C D E);
read all var _num_ into have[c=vnames];
close;
use have(keep= N1-N6);
read all var _num_ into N;
close;
use have(keep= D1-D6);
read all var _num_ into D;
close;
Parm_N={1 -1 -1 -1 -1 -1};
Parm_D={1 -1 -1 -1 -1 -1};
magnitude={-1.05 1.05};
Y=j(nrow(have),1,.);
id=j(ncol(magnitude)#ncol(have),1,blankstr(40));
mean_std=j(ncol(magnitude)#ncol(have),2,.);
mattrib mean_std c={mean std};
idx=0;
do i=1 to ncol(magnitude);
do j=1 to ncol(vnames);
Parm_have=j(1,ncol(have),1);
Parm_have[j]=magnitude[i];
do k=1 to nrow(have);
temp=have[k,];
wgt=(N[k,]*Parm_N`)/(D[k,]*Parm_D`);
wgt=choose(wgt>1,1,wgt);
Y[k]=(Parm_have[1]#temp[1]#
Parm_have[2]#temp[2]#
(Parm_have[3]#temp[3]+1)
-Parm_have[4]#temp[4]
-Parm_have[5]#temp[5])#wgt;
end;
idx=idx+1;
id[idx]=char(magnitude[i])+'*'+vnames[j];
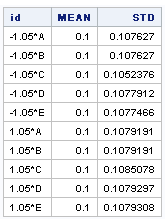
mean_std[idx,1]=mean(Y/sum(Y));
mean_std[idx,2]=std(Y/sum(Y));
end;
end;
print id mean_std[l=''];
quit;- Mark as New
- Bookmark
- Subscribe
- Mute
- RSS Feed
- Permalink
- Report Inappropriate Content
Rick Wicklins book on Simulatimg Data with SAS would be my suggestion.
His blog also has a lot of handy tips. Find the paper Don't Be Loopy by David Cassell as well. It's got some great tips and samples, especially on how to avoid macros. This can be done in a data step. .
Given your our dataset I don't see an issue with using all 70 cases vs 5 at a time.
- Mark as New
- Bookmark
- Subscribe
- Mute
- RSS Feed
- Permalink
- Report Inappropriate Content
Yeah. Using total 70 case , it is not a big deal .
Since it is about data simulation, better post it at SAS/IML Software and Matrix Computations
Here is my IML code, no need Macro. Check it on your own . I have no time.
UPDATE: Fix a problem
data have; input
ID A B C D E N1 N2 N3 N4 N5 N6 D1 D2 D3 D4 D5 D6;
datalines;
1 100 10 0.5 15 10 35 8 6 4 2 1 39 8 5 5 1 2
2 200 11 0.3 25 15 35 8 6 4 2 2 42 7 7 4 2 3
3 300 20 0.4 15 14 40 8 6 4 2 3 53 9 6 5 3 2
4 150 19 0.1 5 19 27 8 6 4 2 4 35 4 9 7 4 4
5 400 40 0.5 35 20 50 8 6 4 2 6 79 17 4 9 1 5
6 900 50 0.4 55 15 70 8 6 4 2 9 85 5 9 4 2 11
7 600 30 -0.5 20 29 60 8 6 4 2 2 62 16 7 5 4 10
8 500 30 0.2 25 17 50 8 6 4 2 3 60 4 9 8 2 5
9 400 30 0.4 19 16 44 8 6 4 2 1 49 8 4 4 5 9
10 700 45 0.3 39 14 34 8 6 4 2 1 38 3 2 5 4 12
;
run;
proc iml;
use have(keep= A B C D E);
read all var _num_ into have[c=vnames];
close;
use have(keep= N1-N6);
read all var _num_ into N;
close;
use have(keep= D1-D6);
read all var _num_ into D;
close;
Parm_N={1 -1 -1 -1 -1 -1};
Parm_D={1 -1 -1 -1 -1 -1};
magnitude={-1.05 1.05};
Y=j(nrow(have),1,.);
id=j(ncol(magnitude)#ncol(have),1,blankstr(40));
mean_std=j(ncol(magnitude)#ncol(have),2,.);
mattrib mean_std c={mean std};
idx=0;
do i=1 to ncol(magnitude);
do j=1 to ncol(vnames);
Parm_have=j(1,ncol(have),1);
Parm_have[j]=magnitude[i];
do k=1 to nrow(have);
temp=have[k,];
wgt=(N[k,]*Parm_N`)/(D[k,]*Parm_D`);
wgt=choose(wgt>1,1,wgt);
Y[k]=(Parm_have[1]#temp[1]#
Parm_have[2]#temp[2]#
(Parm_have[3]#temp[3]+1)
-Parm_have[4]#temp[4]
-Parm_have[5]#temp[5])#wgt;
end;
idx=idx+1;
id[idx]=char(magnitude[i])+'*'+vnames[j];
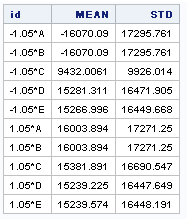
mean_std[idx,1]=mean(Y);
mean_std[idx,2]=std(Y);
end;
end;
print id mean_std[l=''];
quit;- Mark as New
- Bookmark
- Subscribe
- Mute
- RSS Feed
- Permalink
- Report Inappropriate Content
- Mark as New
- Bookmark
- Subscribe
- Mute
- RSS Feed
- Permalink
- Report Inappropriate Content
Thanks Ksharp. I ran the code at work using EG and it worked. (It didn't work on SAS 9.2 or 9.3 for the home computer). I was able to grasp some of it but would require more reading on IML to understand all, let along revise the code. I'm wondering if you can help out for one more thing or point out directions. What I should have asked is once I get Y values under different scenarios of changes, I'll calculate the proportion or share - Y1/sum of Y1-10, Y2/sum of Y, etc.) and get mean and SD of the share. I tried a few things toward the end of the code to aggregate the Want data but none seemed to work. I assumed maybe IML has different programming logic. Any help is appreciated as it is just 0.1 step from what I want.
- Mark as New
- Bookmark
- Subscribe
- Mute
- RSS Feed
- Permalink
- Report Inappropriate Content
"What I should have asked is once I get Y values under different scenarios of changes, I'll calculate the proportion or share - Y1/sum of Y1-10, Y2/sum of Y, etc.) and get mean and SD of the share."
Post your output and formula would better to clarify your question.
This code is almost the same as above .
data have; input
ID A B C D E N1 N2 N3 N4 N5 N6 D1 D2 D3 D4 D5 D6;
datalines;
1 100 10 0.5 15 10 35 8 6 4 2 1 39 8 5 5 1 2
2 200 11 0.3 25 15 35 8 6 4 2 2 42 7 7 4 2 3
3 300 20 0.4 15 14 40 8 6 4 2 3 53 9 6 5 3 2
4 150 19 0.1 5 19 27 8 6 4 2 4 35 4 9 7 4 4
5 400 40 0.5 35 20 50 8 6 4 2 6 79 17 4 9 1 5
6 900 50 0.4 55 15 70 8 6 4 2 9 85 5 9 4 2 11
7 600 30 -0.5 20 29 60 8 6 4 2 2 62 16 7 5 4 10
8 500 30 0.2 25 17 50 8 6 4 2 3 60 4 9 8 2 5
9 400 30 0.4 19 16 44 8 6 4 2 1 49 8 4 4 5 9
10 700 45 0.3 39 14 34 8 6 4 2 1 38 3 2 5 4 12
;
run;
proc iml;
use have(keep= A B C D E);
read all var _num_ into have[c=vnames];
close;
use have(keep= N1-N6);
read all var _num_ into N;
close;
use have(keep= D1-D6);
read all var _num_ into D;
close;
Parm_N={1 -1 -1 -1 -1 -1};
Parm_D={1 -1 -1 -1 -1 -1};
magnitude={-1.05 1.05};
Y=j(nrow(have),1,.);
id=j(ncol(magnitude)#ncol(have),1,blankstr(40));
mean_std=j(ncol(magnitude)#ncol(have),2,.);
mattrib mean_std c={mean std};
idx=0;
do i=1 to ncol(magnitude);
do j=1 to ncol(vnames);
Parm_have=j(1,ncol(have),1);
Parm_have[j]=magnitude[i];
do k=1 to nrow(have);
temp=have[k,];
wgt=(N[k,]*Parm_N`)/(D[k,]*Parm_D`);
wgt=choose(wgt>1,1,wgt);
Y[k]=(Parm_have[1]#temp[1]#
Parm_have[2]#temp[2]#
(Parm_have[3]#temp[3]+1)
-Parm_have[4]#temp[4]
-Parm_have[5]#temp[5])#wgt;
end;
idx=idx+1;
id[idx]=char(magnitude[i])+'*'+vnames[j];
mean_std[idx,1]=mean(Y/sum(Y));
mean_std[idx,2]=std(Y/sum(Y));
end;
end;
print id mean_std[l=''];
quit;
April 27 – 30 | Gaylord Texan | Grapevine, Texas
Registration is open
Walk in ready to learn. Walk out ready to deliver. This is the data and AI conference you can't afford to miss.
Register now and save with the early bird rate—just $795!
Learn how use the CAT functions in SAS to join values from multiple variables into a single value.
Find more tutorials on the SAS Users YouTube channel.
SAS Training: Just a Click Away
Ready to level-up your skills? Choose your own adventure.