- Home
- /
- Programming
- /
- SAS Procedures
- /
- Simulating random walk with actions
- RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
- Mark as New
- Bookmark
- Subscribe
- Mute
- RSS Feed
- Permalink
- Report Inappropriate Content
Hi,
I've created a markov transition matrix that I now want to simulate. Attached should be a picture of a simplified verision of it. There's many more starting and ending states along with more results, but it's essentially just an expanded version of this.

What's the best way to have sas walk through the data as well as keep track of the results?
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- RSS Feed
- Permalink
- Report Inappropriate Content
Here is an example using the smaller 6x6 matrix. Notice that I have included rows for the final states.
The main ideas are
1. Create a POINTS matrix that contains the number of point that you get when you transition from state S to state T
2. For each game, iterate the transition matrix in a DO WHILE loop until you land in one of the ending states. Accumulate points (and maybe other statistics like number of turns) as you go.
3. When you have successfully implemented one game, put a loop DO game = 1 to NUMGAMES around the iteration.
proc iml;
M = {0.05 0.66 0 0 0.29 0 0 0, /* 00 */
0 0.05 0.67 0 0 0.28 0 0, /* 01 */
0 0 0.02 0.68 0 0 0.30 0, /* 02 */
1 0 0 0 0 0 0 0, /* 03 */
0.2 0.03 0.11 0 0.58 0.08 0 0, /* 10 */
0 0.02 0.03 0.14 0 0.33 0.48 0, /* 11 */
0 0 0.02 0.18 0 0 0.21 0.59, /* 12 */
1 0 0 0 0 0 0 0 }; /* 13 */
points = I(nrow(M)); /* identity matrix */
points[5,1] = 2; /* set off-diagonal elements of transitions */
/* row M[i, ] contains probabilities for transitioning from state i */
/* play one game */
state = 1; /* start in state 1 */
cnt = 1;
pts = 0; /* points for this game */
do while (state ^= 3 & state ^= 6);
newState = randfun(1, "Table", M[state,] ); /* new state */
pts = pts + points[state, newState];
cnt = cnt + 1;
state = newState;
end;
print pts cnt state;
- Mark as New
- Bookmark
- Subscribe
- Mute
- RSS Feed
- Permalink
- Report Inappropriate Content
calling @Rick_SAS
- Mark as New
- Bookmark
- Subscribe
- Mute
- RSS Feed
- Permalink
- Report Inappropriate Content
The easiest way is to use the SAS/IML matrix language, since applying a transition matrix to the current state is a matrix-vector computation. To get started, see the example in the article
"Markov transition matrices in SAS/IML"
- Mark as New
- Bookmark
- Subscribe
- Mute
- RSS Feed
- Permalink
- Report Inappropriate Content
So then how would I incoroprate the results into that?
- Mark as New
- Bookmark
- Subscribe
- Mute
- RSS Feed
- Permalink
- Report Inappropriate Content
You need to tell us your level of expertise and the tools you have available. If you have SAS/IML and know about matrix operations, I can move this discussion to the SAS/IML Support Community.
If you prefer to use the DATA step to solve this problem, then say so and someone can help you use arrays to solve this problem.
In either case, you are going to use the "Table" distribution to generate the next state from the current state, The rows of the transition matrix give the probability of transitioning to the other states. I recommend that you add two other rows for the transition to the 03 and 13 states.
In matrix notation, if M is the 8x8 transition matrix and s is the current state of the system, then
s = randfun(1, "Table", M[s, ]);
updates the state. You just need to put it in a loop and add logic to accumulate points.
- Mark as New
- Bookmark
- Subscribe
- Mute
- RSS Feed
- Permalink
- Report Inappropriate Content
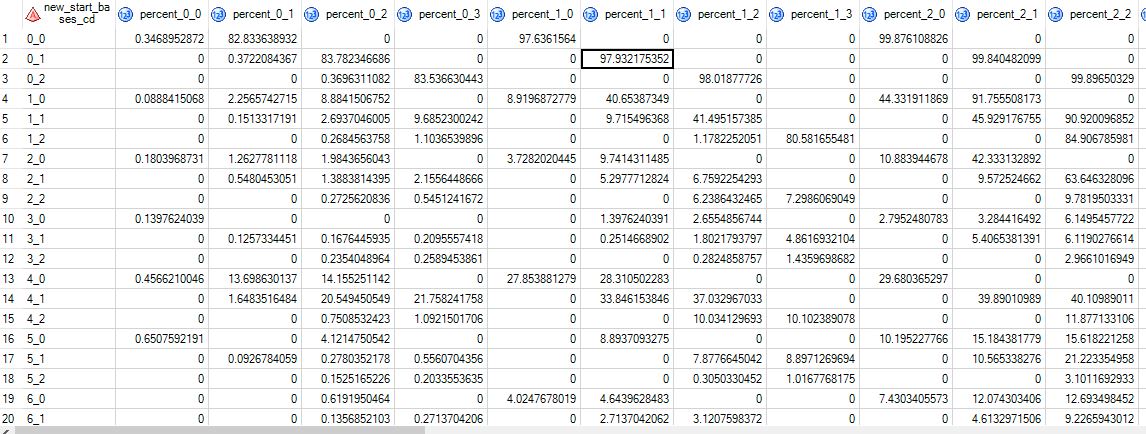
Hi Rick, thanks for your help. I do have some experience with SAS, but am nowhere near being an expert. I do have SAS/IML and have a basic understanding of matrix operations. I think the article you linked to helped clarify a few points. The image posted was just a simplification of what we actually have. Attached is a more accurate representation of the matrix, which is actually 24 rows by 32 columns. Currently they're displaying the row cumulative percent which I think is the harder method you talk about in the article.
Between your article and some more reading what we have in mind is running a loop to generate a random number to select our first end state. We would then set the end state as our next start state and repeat the process, as certain end states can only be reached from a particular start state. For a more concrete example: suppose we start at state 0_0 then transtition to 1_0. The probabilities of transitioning out of 1_0 are stored in that row. Thus we would want to generate another random number to select our end state, which then becomes our next row. Is that possible to do in both the data step or IML, or is there a better way to approach this?
Thank you.
- Mark as New
- Bookmark
- Subscribe
- Mute
- RSS Feed
- Permalink
- Report Inappropriate Content
Here is an example using the smaller 6x6 matrix. Notice that I have included rows for the final states.
The main ideas are
1. Create a POINTS matrix that contains the number of point that you get when you transition from state S to state T
2. For each game, iterate the transition matrix in a DO WHILE loop until you land in one of the ending states. Accumulate points (and maybe other statistics like number of turns) as you go.
3. When you have successfully implemented one game, put a loop DO game = 1 to NUMGAMES around the iteration.
proc iml;
M = {0.05 0.66 0 0 0.29 0 0 0, /* 00 */
0 0.05 0.67 0 0 0.28 0 0, /* 01 */
0 0 0.02 0.68 0 0 0.30 0, /* 02 */
1 0 0 0 0 0 0 0, /* 03 */
0.2 0.03 0.11 0 0.58 0.08 0 0, /* 10 */
0 0.02 0.03 0.14 0 0.33 0.48 0, /* 11 */
0 0 0.02 0.18 0 0 0.21 0.59, /* 12 */
1 0 0 0 0 0 0 0 }; /* 13 */
points = I(nrow(M)); /* identity matrix */
points[5,1] = 2; /* set off-diagonal elements of transitions */
/* row M[i, ] contains probabilities for transitioning from state i */
/* play one game */
state = 1; /* start in state 1 */
cnt = 1;
pts = 0; /* points for this game */
do while (state ^= 3 & state ^= 6);
newState = randfun(1, "Table", M[state,] ); /* new state */
pts = pts + points[state, newState];
cnt = cnt + 1;
state = newState;
end;
print pts cnt state;
- Mark as New
- Bookmark
- Subscribe
- Mute
- RSS Feed
- Permalink
- Report Inappropriate Content
Rick, that worked perfectly; thank you. I just have one more question, then I should be set.
Currently our transition matrix is rectangular. Is this a valid workaround, or do we need to add rows to make it square?
state = 1; /* start in state 1 */
cnt = 1;
pts = 0; /* points for this game */
sentinel = 0;
do while (sentinel ^= 1);
newState = randfun(1, "Table", M[state,] ); /* new state */
pts = pts + points[state, newState];
cnt = cnt + 1;
if (newState = 3 | newState =6) then sentinel = 1;
state = newState;
end;
- Mark as New
- Bookmark
- Subscribe
- Mute
- RSS Feed
- Permalink
- Report Inappropriate Content
It looks fine. You can try it and see if it works.
You are free to use non-square matrices. If you only have two states, you might consider using
do while (newState ^= 3 & newState ^=6);
but if you are going to have many states that end the game then your 'sentinel' way is probably clearer.
- Mark as New
- Bookmark
- Subscribe
- Mute
- RSS Feed
- Permalink
- Report Inappropriate Content
Under the @Rick_SAS 's guidance, it seems it is very easy.
data x;
input _1-_6;
cards;
0.05 0.66 0 0 0.29 0
0 0.05 0.67 0 0 0.28
0 0 0.02 0.68 0 0.3
0.2 0.03 0.11 0 0.58 0.08
0 0.02 0.03 0.14 0.48 0.33
0 0 0.02 0.18 0.21 0.59
;
run;
data point;
input s e point;
cards;
1 2 1
1 1 1
2 2 1
1 4 2
;
run;
%let start=1;
%let steps=20;
proc iml;
use x;
read all var _all_ into x;
close;
use point;
read all var {s e point};
close;
start=&start;
points=0;
call randseed(12345678);
do i=1 to &steps;
end=randfun(1, "Table", x[start, ]);
idx=(s=start & e=end);
if any(idx) then points=points+point[loc(idx)];
msg="steps="+char(i)+",start="+char(start)+',end='+char(end)+',points='+char(points);
print msg;
if end=3 then start=&start;
else start=end;
end;
quit;
April 27 – 30 | Gaylord Texan | Grapevine, Texas
Registration is open
Walk in ready to learn. Walk out ready to deliver. This is the data and AI conference you can't afford to miss.
Register now and save with the early bird rate—just $795!
Learn the difference between classical and Bayesian statistical approaches and see a few PROC examples to perform Bayesian analysis in this video.
Find more tutorials on the SAS Users YouTube channel.
SAS Training: Just a Click Away
Ready to level-up your skills? Choose your own adventure.