- Home
- /
- Programming
- /
- SAS Procedures
- /
- Question Related to Tolerance Intervals
- RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
- Mark as New
- Bookmark
- Subscribe
- Mute
- RSS Feed
- Permalink
- Report Inappropriate Content
Hello,
I wonder why there is no tolerance interval for linear regression (GLM) and for nonlinear regression (NLIN).
I tried with the paper of Young DS (2010) used in R-project.
But I am not sure, there seem to be more papers on tolerance intervals with different (aproximate) formulae;
so if SAS had one, this would be a nice reference.
Kind regards
P.S.
NOTE: SAS (r) Proprietary Software 9.4 (TS1M1)
NOTE: This session is executing on the X64_7PRO platform.
- Mark as New
- Bookmark
- Subscribe
- Mute
- RSS Feed
- Permalink
- Report Inappropriate Content
The SAS PROC GLM guide mentions the TOLERANCE option on page 2472. See also options for generating confidence intervals, on that same page.
You might have to play around with it a bit. If TOLERANCE doesn't produce the intervals you are looking for, you might have to use ALPHA=p and customize the p value.
There are also tolerance intervals for the CAPABILITY procedure; see here and here.
- Mark as New
- Bookmark
- Subscribe
- Mute
- RSS Feed
- Permalink
- Report Inappropriate Content
See below my try: some random data
Plotted are the data together with
The regression line (black), the confidence interval (green short dashed), prediction interval (red), tolerance interval (blue dashed).
I am not sure, if Young's formula is the best. If there was an implementation in SAS I would take these as being reliable...
Kind regards, Armin Böhrer
[Plot of plot_value by time identified by plot_ident]
- Mark as New
- Bookmark
- Subscribe
- Mute
- RSS Feed
- Permalink
- Report Inappropriate Content
Hi Armin, I understand now that PROC CAPABILITY is more for quality analysis, and not what you are looking for.
The image isn't showing up... I'm not sure it uploaded correctly.
- Mark as New
- Bookmark
- Subscribe
- Mute
- RSS Feed
- Permalink
- Report Inappropriate Content
Figure added as an attachment
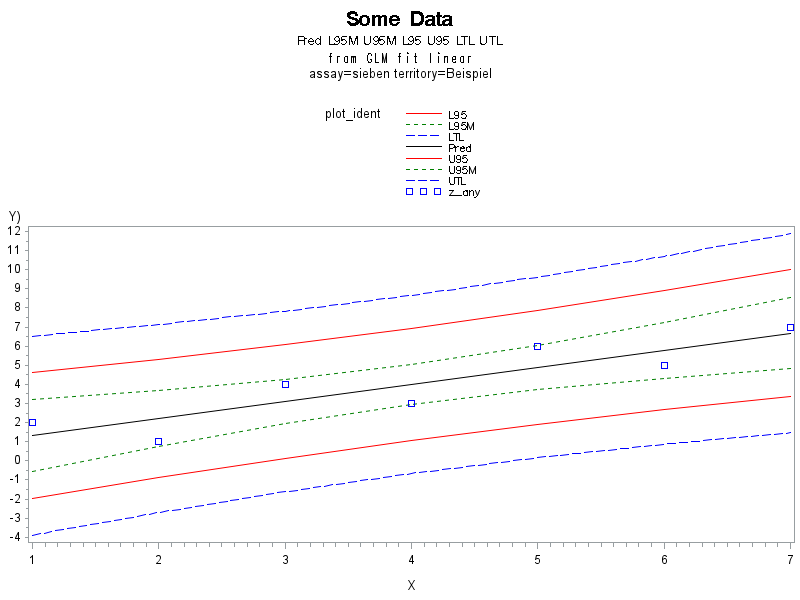
- Mark as New
- Bookmark
- Subscribe
- Mute
- RSS Feed
- Permalink
- Report Inappropriate Content
The TOLERANCE option on the PROC GLM MODEL statement has nothing to do with statistical tolerance intervals. It refers to a quantity that is relevant in numerical matrix computations.
There was a similar question asked recently. See the reply by @FreelanceReinh who mentions a SAS macro at
- Mark as New
- Bookmark
- Subscribe
- Mute
- RSS Feed
- Permalink
- Report Inappropriate Content
Could you provide a full reference? Kind of hard to search for "Young DS (2010)"
- Mark as New
- Bookmark
- Subscribe
- Mute
- RSS Feed
- Permalink
- Report Inappropriate Content
Hello, the Reference
„Young, D. S. (2010), tolerance: An R Package for Estimating Tolerance Intervals, Journal of Statistical Software, 36(5), 1–39.”
is one among others of the references listed in the R-package ‘tolerance’.
- Mark as New
- Bookmark
- Subscribe
- Mute
- RSS Feed
- Permalink
- Report Inappropriate Content
The formulas on p. 32 of your reference indicated that the tolerance limits can be derived from the GLM output by doing the following:
1. Output the predicted values (P=y_hat) and the standard error of the individual predicted values (STDI=stdErr_yhat)
2. Use ODS OUPUT to obtain the RMSE (sigma_hat), n (nonmissing obs), and p (number of regression parameters)
Then write a DATA step to compute two-sided tolerance limits:
1. Effective number of obs n_i = sigma_hat**2 / stdErr_yhat**2
2. Use the QUANTILE function to obtain the Pth quantile of the noncentral chi-square distrib with 1 dof and noncentrality parameter 1/n_i
3. Compute k_2i
4. Form the tolerance limits as L = y_hat - sigma_hat * k_2i and U = y_hat + sigma_hat * k_2i
To overlay the data, the predicted values, and the tolerance limits, use PROC SGPLOT with three statements:
band x=x lower=L upper=U;
scatter x=x y=y;
series x=y y=y_hat;
- Mark as New
- Bookmark
- Subscribe
- Mute
- RSS Feed
- Permalink
- Report Inappropriate Content
Thank you for your answer, and how to use it with GML.
As you see from my plot from Wednesday last week, I had some implementation too.
(I did not make a literature search, Young's paper, which I quoted, is one out of (possibly) many, and probably several possible approximate formulae exist; so it is not clear to me, which paper/approximation/formula to use, e.g., STDP or STDI, or use other definitions of n_i etc.?)
My original intention by the click on the button "software suggestion" on the SAS-webside was, that
I thought that SAS could implement a "reference TI for regression" like they have for "TI of samples" in PROC CAPABILITY.
April 27 – 30 | Gaylord Texan | Grapevine, Texas
Registration is open
Walk in ready to learn. Walk out ready to deliver. This is the data and AI conference you can't afford to miss.
Register now and save with the early bird rate—just $795!
Learn the difference between classical and Bayesian statistical approaches and see a few PROC examples to perform Bayesian analysis in this video.
Find more tutorials on the SAS Users YouTube channel.
SAS Training: Just a Click Away
Ready to level-up your skills? Choose your own adventure.


