- RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
- Mark as New
- Bookmark
- Subscribe
- Mute
- RSS Feed
- Permalink
- Report Inappropriate Content
proc iml;
/* the number of assets */
n=2;
/* riskless rate - Government's bond rate */
f=0.02 ;
/* Start Calculated */
/* two assets and populate data */
asset=j(100,n,.);
call randseed(1234);
call randgen(asset,'normal');
/* the expect return of two assets (mean) */
return=asset[:,];
/* the variance and covariance of two assets */
cov=cov(asset);
/* the variance of portfolio */
new_cov=2#cov-diag(vecdiag(cov));
col=col(new_cov);
row=row(new_cov);
idx=loc(col>=row);
p_cov=row[idx]||col[idx]||new_cov[idx];
/* p[1] is expect return of porfolio
p[2] is variance of porfolio */
p=j(1,2,.);
/* the tangency portfolio */
start max_slope(x) global(f,p,p_cov,return);
p[1]=(return#x)[+];
p[2]=(x[p_cov[,1]]#x[p_cov[,2]]#p_cov[,3])[+];
/*riskless rate's variance is zero*/
k=(p[1]-f)/p[2];
return (k);
finish;
ods output IterHist=IterHist;
con=repeat({0,1,1},1,n)||{. .,. .,0 1};
x=j(1,n,1/n);
optn={1 3};
call nlptr(xres,rc,"max_slope",x,optn,con);
quit;
/************************************/
/************************************/
/************************************/
/************************************/
/* Test if it is tangency portfolio */
/* Take two assets above for example*/
data _null_;
set IterHist;
call symputx('k',OptCrit);
call symputx('f','0.02');
run;
proc iml;
/* The same code as above. Start */
n=2;
f=0.02 ;
asset=j(100,n,.);
call randseed(1234);
call randgen(asset,'normal');
return=asset[:,];
cov=cov(asset);
new_cov=2#cov-diag(vecdiag(cov));
col=col(new_cov);
row=row(new_cov);
idx=loc(col>=row);
p_cov=row[idx]||col[idx]||new_cov[idx];
/* The same code as above. End*/
p=j(100,2);
x=j(1,n,.);
do i=1 to 100;
x[1]=0.01#i;
x[2]=1-x[1];
p[i,1]=(return#x)[+];
p[i,2]=(x[p_cov[,1]]#x[p_cov[,2]]#p_cov[,3])[+];
end;
create test from p[c={return variance}];
append from p;
close;
quit;
ods graphics/reset;
proc sgplot data=test;
series x=variance y=return/ lineattrs=(thickness=2) legendlabel='Portfolio' curvelabel='Efficient Frontier';
lineparm x=0 y=&f slope=&k/ legendlabel='Tangency Portfolio' lineattrs=graphdata2(thickness=2);
refline &f / axis=y;
xaxis label='Portfolio Variance';
yaxis label='Portfolio Return';
run;
/* Bingo !!!! */
/************************************/
/************************************/
/************************************/
/************************************/
- Mark as New
- Bookmark
- Subscribe
- Mute
- RSS Feed
- Permalink
- Report Inappropriate Content
Thanks for this program. If I used correlated assets, I don't seem to get the correct tangency curve. What needs to change if you use the following?
Sigma = {1 0.2, 0.2 1};
mu = {0 0};
asset = randnormal(100, mu, Sigma); /* generate obs from MVN(mu, Sigma) */
- Mark as New
- Bookmark
- Subscribe
- Mute
- RSS Feed
- Permalink
- Report Inappropriate Content
@Rick,
You are right. I just simulate lots of portfolios ,and can't guarantee you get efficient portfolio frontier.
If you want get that efficient portfolio frontier, you need solve lots of optimize problem.
Something like :
return=asset[:,];
start min_variance(x) global(cov);
/*a portfolio 's variance*/
k=x*cov*x`;
return (k);
finish;
do r=0.01 to 0.1;
/*constraint portfolio's return is 0.01,0.02,0.03,0.04...........*/
/* return*x`=0.01,0.02,0.03,0.04 */
/*change the following CON, I forgot syntax*/
con=repeat({0,1,1},1,n)||{. .,. .,0 return};
x=j(1,n,1/n);
optn={1 3};
call nlptr(xres,rc,"min_variance",x,optn,con);
print xres ;
end;
- Mark as New
- Bookmark
- Subscribe
- Mute
- RSS Feed
- Permalink
- Report Inappropriate Content
Finally I have some time to go through.
Better make mu great than 0 .
The code above is too old.
You can get my new code at SAS Global Forum 2017 ,
Search "Get Tangency Portfolio" at SGF2017.
proc iml;
Sigma = {1 0.2, 0.2 1};
mu = {0.2 0.2};
asset = randnormal(10000, mu, Sigma); /* generate obs from MVN(mu, Sigma) */
/* the expect return of two assets (mean) */
return=asset[:,];
/* the variance and covariance of two assets */
cov=cov(asset);
start min_variance(x) global(cov);
return (x*cov*x`);
finish;
x=j(1,2,0.5);
optn={0 1 0.001};
do r=0.02 to 0.34 by 0.02;
con={ 0 0 . .,
1 1 . .}//
(return||0||r);
call nlpnrr(rc,xres,"min_variance",x,optn,con);
r_cov=r_cov//(r||xres*cov*xres`);
end;
print r_cov;
call series x=r_cov[,2] y=r_cov[,1];
quit;- Mark as New
- Bookmark
- Subscribe
- Mute
- RSS Feed
- Permalink
- Report Inappropriate Content
This is extremely helpful, thank you. I ran some simulations with 3 asset classes based on the code from the 2017 sas paper, and it's very convenient!
I have a question - I noticed that in the final graph (Tangency with EF), the "Star" i.e., the tangent portfolio, doesn't lie on the EF (blue line), as the number of assets increases. I tried it for 15 to 20 asset classes, the "Start" gets pushed more and more on the top half of the graph, away from EF. I even checked the Frontier and Tangency datasets, and the tangent (return, std) values, do not feature in the frontier data in these instances.
Any idea what's the reason for this?
PS: I didn't change anything from your code. just increased N from 3 to 15, and so on. Even the number of simulated rows (10,000) and rest of the distribution parameters are the same.
- Mark as New
- Bookmark
- Subscribe
- Mute
- RSS Feed
- Permalink
- Report Inappropriate Content
Hi,
The code posted yesterday is not right because I did not consider constrain(sum of these proportional =1) when to calculated Efficient Frontier.
Now The code has been updated.
Try the following code .
You need to change 'r' to be small enough to make your model convergency.
do r=0 to 0.04 by 0.001; /*expect return of portfolio*/
Hi. That long time ago, my memory is almost faded away. As I said I just simulate lots and lots of portfolios ,NOT actually calculated Efficient Frontier. If you want it you need solve many optimal problems.
Here is an example:
%let n=20;
proc iml;
/* the number of assets */
n=&n.;
/* riskless rate - Government's bond rate */
f=0.02 ;
/* Start Calculated */
/* two assets and populate data */
asset=j(1000,n,.);
call randseed(1234);
call randgen(asset,'normal');
/* the expect return of two assets (mean) */
return=asset[:,];
/* the variance and covariance of two assets */
cov=cov(asset);
/* p[1] is expect return of porfolio
p[2] is variance of porfolio */
p=j(1,2,.);
/* the tangency portfolio */
start max_slope(x) global(f,p,cov,return);
p[1]=(return#x)[+];
p[2]=x*cov*x`;
/*riskless rate's variance is zero*/
k=(p[1]-f)/p[2];
return (k);
finish;
ods output IterHist=IterHist;
con=repeat({0,1,1},1,n)||{. .,. .,0 1}; /*<---- sum of these proportional =1 */
x=j(1,n,1/n);
optn={1 3};
call nlptr(xres,rc,"max_slope",x,optn,con);
quit;
/************************************/
/************************************/
/************************************/
/************************************/
/* Test if it is tangency portfolio */
/* Take two assets above for example*/
data _null_;
set IterHist;
call symputx('k',OptCrit);
call symputx('f','0.02');
run;
proc iml;
/* The same code as above. Start */
n=&n.;
f=0.02 ;
asset=j(1000,n,.);
call randseed(1234);
call randgen(asset,'normal');
return=asset[:,];
cov=cov(asset);
/* The same code as above. End*/
start min_variance(x) global(cov);
return (x*cov*x`);
finish;
x=j(1,n,1/n);
optn={0 1 0.001};
do r=0 to 0.04 by 0.001; /*expect return of portfolio*/
con=(repeat({0,1,1},1,n)||{. .,. .,0 1})//(return||0||r);
call nlpnrr(rc,xres,"min_variance",x,optn,con) ;
r_cov=r_cov//(r||xres*cov*xres`);
end;
create test from r_cov[c={return variance}];
append from r_cov;
close;
quit;
ods graphics/reset;
proc sgplot data=test;
series x=variance y=return/ lineattrs=(thickness=2) legendlabel='Portfolio' curvelabel='Efficient Frontier';
lineparm x=0 y=&f slope=&k/ legendlabel='Tangency Portfolio' lineattrs=graphdata2(thickness=2);
refline &f / axis=y;
xaxis label='Portfolio Variance';
yaxis label='Portfolio Return';
run;
/* Bingo !!!! */
/************************************/
/************************************/
/************************************/
/************************************/
Actually it is a Quadratic Programming. You could solve this mean-variance model by SAS/IML builded-in functions : CALL LCP() or CALL QPSOLVE() or CALL NLPQUA()
https://blogs.sas.com/content/iml/2024/07/24/new-quadratic-optimization.html
https://blogs.sas.com/content/iml/2024/07/15/isotonic-regression.html
- Mark as New
- Bookmark
- Subscribe
- Mute
- RSS Feed
- Permalink
- Report Inappropriate Content
Thank you so much for such a quick and detailed response @Ksharp (amazing after 7 years :)).
I will definitely check and try this out.
Thanks again.
- Mark as New
- Bookmark
- Subscribe
- Mute
- RSS Feed
- Permalink
- Report Inappropriate Content
As I posted with pictures.
- Mark as New
- Bookmark
- Subscribe
- Mute
- RSS Feed
- Permalink
- Report Inappropriate Content
Thank you @Ksharp .
I ran this with a few modifications
- the part to create assets returns data (I am using market data)
- used NLPNRA for both deriving and validating the tangency portfolio (was having trouble with convergence with NLPTR and NLPRR)
- adjusted the range of r in the simulation to get the display area in the graph.
It works!
Again, thanks a ton!
- Mark as New
- Bookmark
- Subscribe
- Mute
- RSS Feed
- Permalink
- Report Inappropriate Content
Hi @Ksharp , couple of quick clarifications:
1. On Portfolio Variance: Should it be
p[2]=x*cov*x`or
p[2]=sqrt(x*cov*x`)usually, Sqrt would be the standard deviation, however I was looking back at the 2017 paper, and there the variance has been defined with Sqrt.
2. Calculation of K Slope (Sharpe Ratio);
k=(p[1]-f)/p[2];where
p[2]=x*cov*x`; Sharpe ratio is defined in terms of Standard deviation. So, if this is the definition of p[2], then should the Sharpe ratio be?
k=(p[1]-f)/p[2];
/*where p[2]=sqrt(x*cov*x`)*/Thanks in advance.
- Mark as New
- Bookmark
- Subscribe
- Mute
- RSS Feed
- Permalink
- Report Inappropriate Content
1)
Portfolio Variance should be p[2]=x*cov*x` .
Portfolio standard deviation should be p[2]=sqrt(x*cov*x`).
In the picture with 2017 paper should be STD at X axis side, if it was not , that might be my mistake.
2)
Calculation of K Slope (Sharpe Ratio);
Yes. you are right. But here I only consider about Tangency Point(a.k.a the biggest slope with Efficient Frontier Curve).
Here I calculated Efficient Frontier Curve with Portfolio Variance, not STD.
Therefore you need to use Variance to calculate slope K ,not STD.
If you get Efficient Frontier Curve with Portfolio STD. then you should use p[2]=sqrt(x*cov*x`) to get slope K as I showed in my paper.
- Mark as New
- Bookmark
- Subscribe
- Mute
- RSS Feed
- Permalink
- Report Inappropriate Content
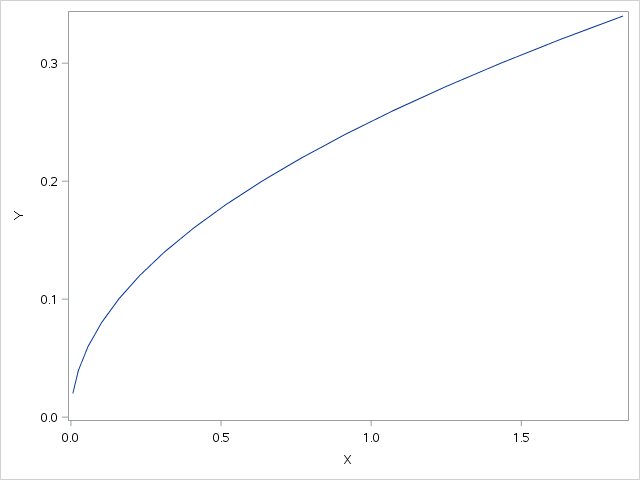
As you wish I used Portfolio Standard Deviation to calcualte Efficient Frontier.
But it looks like it is not easy to get convergency of model with STD. So I suggest to use Portfolio Variance ,not STD .
%let n=20;
proc iml;
/* the number of assets */
n=&n.;
/* riskless rate - Government's bond rate */
f=0.02 ;
/* Start Calculated */
/* two assets and populate data */
asset=j(1000,n,.);
call randseed(1234);
call randgen(asset,'normal');
/* the expect return of two assets (mean) */
return=asset[:,];
/* the variance and covariance of two assets */
cov=cov(asset);
/* p[1] is expect return of porfolio
p[2] is variance of porfolio */
p=j(1,2,.);
/* the tangency portfolio */
start max_slope(x) global(f,p,cov,return);
p[1]=(return#x)[+];
p[2]=sqrt(x*cov*x`);
/*riskless rate's variance is zero*/
k=(p[1]-f)/p[2];
return (k);
finish;
ods output IterHist=IterHist;
con=repeat({0,1,1},1,n)||{. .,. .,0 1}; /*<---- sum of these proportional =1 */
x=j(1,n,1/n);
optn={1 3};
call nlpnra(xres,rc,"max_slope",x,optn,con);
quit;
/************************************/
/************************************/
/************************************/
/************************************/
/* Test if it is tangency portfolio */
/* Take two assets above for example*/
data _null_;
set IterHist;
call symputx('k',OptCrit);
call symputx('f','0.02');
run;
proc iml;
/* The same code as above. Start */
n=&n.;
f=0.02 ;
asset=j(1000,n,.);
call randseed(1234);
call randgen(asset,'normal');
return=asset[:,];
cov=cov(asset);
/* The same code as above. End*/
start min_std(x) global(cov);
return (sqrt(x*cov*x`));
finish;
x=j(1,n,1/n);
optn={0 1 0.001};
do r=0 to 0.046 by 0.001; /*expect return of portfolio*/
con=(repeat({0,1,1},1,n)||{. .,. .,0 1})//(return||0||r); /*<---- sum of these proportional =1 */
call nlpnra(rc,xres,"min_std",x,optn,con) ;
r_cov=r_cov//(r||sqrt(xres*cov*xres`));
end;
create test from r_cov[c={return std}];
append from r_cov;
close;
quit;
ods graphics/reset;
proc sgplot data=test;
series x=std y=return/ lineattrs=(thickness=2) legendlabel='Portfolio' curvelabel='Efficient Frontier';
lineparm x=0 y=&f slope=&k/ legendlabel='Tangency Portfolio' lineattrs=graphdata2(thickness=2);
refline &f / axis=y;
xaxis label='Portfolio STD';
yaxis label='Portfolio Return';
run;
/* Bingo !!!! */
/************************************/
/************************************/
/************************************/
/************************************/
- Mark as New
- Bookmark
- Subscribe
- Mute
- RSS Feed
- Permalink
- Report Inappropriate Content
Thanks @Ksharp for clearing up the Variance v. STD, and K v Sharpe ratio topics.
I have tried both ways, and you are correct - Variance approach is the friendlier one.
Regarding QP : I have set up the QP code, but still figuring out ways to get all the outputs together in one go. I also have to validate that QP is getting proper data based on how I have defined the assets in IML. WIP!
Thanks again.
- Mark as New
- Bookmark
- Subscribe
- Mute
- RSS Feed
- Permalink
- Report Inappropriate Content
Good Luck.
April 27 – 30 | Gaylord Texan | Grapevine, Texas
Registration is open
Walk in ready to learn. Walk out ready to deliver. This is the data and AI conference you can't afford to miss.
Register now and save with the early bird rate—just $795!
- Discovery-based Investigation in SAS Visual Investigator – Your Guide to Better Searches | 20-Jan-2026
- SAS Bowl LVIII, SAS Viya Copilot | 21-Jan-2026
- Ask the Expert: Wie der SAS Visual Analytics Copilot Ihre Arbeit beschleunigt! | 22-Jan-2026
- Ask the Expert: The AI Advantage: How SAS Customer Intelligence 360 Solves Real Marketing Challenges | 27-Jan-2026
- DCSUG presents SAS OnDemand for Academics: the Easy Way to Learn SAS For Free for Students, Educator | 27-Jan-2026
- Ask the Expert: How to Supercharge Enterprise Agentic Workflows With SAS Retrieval Agent Manager | 05-Feb-2026
- Ask the Expert: Implementing a Digital Twin for the Monopoly Board Game Using SAS® Viya® | 12-Feb-2026