- RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
- Mark as New
- Bookmark
- Subscribe
- Mute
- RSS Feed
- Permalink
- Report Inappropriate Content
Hi,
I have a question regarding the capabilites of proc iml. Suppose I have a matrix of probabilites, then want to multiply each cell directly by a scalar matrix, so that only some of the probabilites go up while some remain the same. For example:
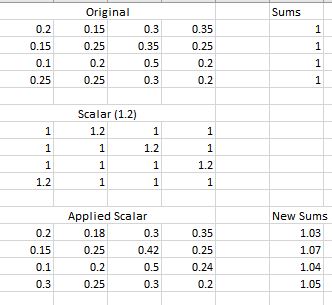
Now, I'd like to multiply the other values in each row by a scalar in order for each row to still sum to one. But the scalar also needs to be computed for each row.
This can be accomplished with excel's solver, as shown:
Would this be possible to accomplish in IML, or would I need to look to a different procedure, or is there a better way to go about this?
Attached is code to set up the beginning matrices in SAS:
proc iml;
A = { 0.20 0.15 0.30 0.35,
0.15 0.25 0.35 0.25,
0.10 0.20 0.50 0.20,
0.25 0.25 0.30 0.20};
B = A[ ,+];
C = { 1.0 1.2 1.0 1.0,
1 1 1.2 1.0,
1 1 1 1.2,
1.2 1 1 1};
D = A#C;
E = D[ ,+];
Thank you,
Justin
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- RSS Feed
- Permalink
- Report Inappropriate Content
The problem is that (H ^= 0) first evaluates to a matrix of zeros and ones, so when this is applied to D with elementwise multiplication it either preserves the existing values in D, or sets them to zero.
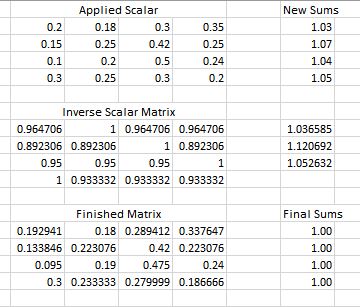
It is possible to get the Inverse Scalar Matrix using a small trick. First subtract one from G, next calculate H as you have above, finally add back the one. The overall effect is to place a one, rather than a zero, at every location in H corresponding to one of the modified values.
F = (D#(C^=1))[,+];
G = (1-F)/(E-F);
H = (G-1)#(C=1) + 1;
J = D # H;
print H [l='Inverse Scalar Matrix'], J [l='Finished Matrix'];- Mark as New
- Bookmark
- Subscribe
- Mute
- RSS Feed
- Permalink
- Report Inappropriate Content
I think you are over complicating things by suggesting you need to use the Excel solver. Once you know the sum of values in each row that have been increased (F), then it is a simple calculation to find the row scalars (G).
F = (D#(C^=1))[,+];
G = (1-F)/(E-F);
print G;- Mark as New
- Bookmark
- Subscribe
- Mute
- RSS Feed
- Permalink
- Report Inappropriate Content
That works great; thank you.
Now to apply that to the new matrix, so that the values of G multiply all the other cells in D, I tried:
H = G#(C=1); /*To create similar scalar matrix */
J = D#(H ^= 0);
But J isn't showing the values I'd like.
- Mark as New
- Bookmark
- Subscribe
- Mute
- RSS Feed
- Permalink
- Report Inappropriate Content
The problem is that (H ^= 0) first evaluates to a matrix of zeros and ones, so when this is applied to D with elementwise multiplication it either preserves the existing values in D, or sets them to zero.
It is possible to get the Inverse Scalar Matrix using a small trick. First subtract one from G, next calculate H as you have above, finally add back the one. The overall effect is to place a one, rather than a zero, at every location in H corresponding to one of the modified values.
F = (D#(C^=1))[,+];
G = (1-F)/(E-F);
H = (G-1)#(C=1) + 1;
J = D # H;
print H [l='Inverse Scalar Matrix'], J [l='Finished Matrix'];- Mark as New
- Bookmark
- Subscribe
- Mute
- RSS Feed
- Permalink
- Report Inappropriate Content
It looks like you want SOLVE() function.
proc iml;
A = { 0.20 0.15 0.30 0.35,
0.15 0.25 0.35 0.25,
0.10 0.20 0.50 0.20,
0.25 0.25 0.30 0.20};
C = { 1.0 1.2 1.0 1.0,
1 1 1.2 1.0,
1 1 1 1.2,
1.2 1 1 1};
D=A#C;
Y=j(nrow(A),1,1);
X=solve(D,Y);
want=D#X`;
print want (want[,+]);
quit;
WANT
0.2467064 0.0667512 0.3381478 0.3483947 1
0.1850298 0.0927101 0.4734069 0.2488533 1
0.1233532 0.074168 0.5635796 0.2388992 1
0.3700595 0.0927101 0.3381478 0.1990827 1
April 27 – 30 | Gaylord Texan | Grapevine, Texas
Registration is open
Walk in ready to learn. Walk out ready to deliver. This is the data and AI conference you can't afford to miss.
Register now and lock in 2025 pricing—just $495!
- Ask the Expert: Marketing Decisions Excellence: Turning Insights Into Business Impact | 16-Dec-2025
- SAS Bowl LVII, SAS Data Maker and Synthetic Data | 17-Dec-2025
- Ask the Expert: Real-Time Agent Assist and Next-Gen Strategy for Financial Services | 15-Jan-2026
- Discovery-based Investigation in SAS Visual Investigator – Your Guide to Better Searches | 20-Jan-2026
- Ask the Expert: The AI Advantage: How SAS Customer Intelligence 360 Solves Real Marketing Challenges | 27-Jan-2026
- DCSUG presents SAS OnDemand for Academics: the Easy Way to Learn SAS For Free for Students, Educator | 27-Jan-2026
- SAS Innovate 2026 | Grapevine, Texas | 27-Apr-2026