- Home
- /
- Analytics
- /
- Forecasting
- /
- description of SARIMA model
- RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
- Mark as New
- Bookmark
- Subscribe
- Mute
- RSS Feed
- Permalink
- Report Inappropriate Content
I have built a proper model through the Arima process step, but I don't know how to formally and correctly describe the model.
this is my final arima model,it should name "ARIMA(1,1,1)(1,1,1)52" or another???
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- RSS Feed
- Permalink
- Report Inappropriate Content
Hello @Phoenix_LJ ,
I am assuming you are familiar with the backshift notation and polynomials in the backshift operator.
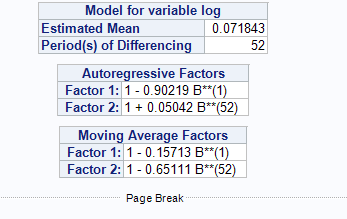
Here's the formulae of your ARIMA(1,0,1)(1,1,1)52 model :
- Z_t =
( 1 - B )( 1 - B**52 ) Y_t - ( 1 - 0.90219B ) ( 1 + 0.05042B**52) Z_t = 0.071843 + (1 - 0.15713B ) ( 1 - 0.65111B**52 ) e_t
This is indeed a SARIMA model, i.e. Seasonal ARIMA (Auto-Regressive Integrated Moving Average) model with :
- seasonal differencing (once on 52 periods = simple seasonal differencing). The degree d of the seasonal differencing is 1 and s=52 is the length of the seasonal cycle.
- 1 is the order of the autoregressive part
- 1 is the order of the seasonal autoregressive part
- 1 is the order of the moving-average process
- 1 is the order of the seasonal moving-average process
- e_t is the independent disturbance, also called the random error
- you have no transfer functions as it is not SARIMAX (with some extra X-input time series)
Kind regards,
Koen
- Mark as New
- Bookmark
- Subscribe
- Mute
- RSS Feed
- Permalink
- Report Inappropriate Content
Hello @Phoenix_LJ ,
I am assuming you are familiar with the backshift notation and polynomials in the backshift operator.
Here's the formulae of your ARIMA(1,0,1)(1,1,1)52 model :
- Z_t =
( 1 - B )( 1 - B**52 ) Y_t - ( 1 - 0.90219B ) ( 1 + 0.05042B**52) Z_t = 0.071843 + (1 - 0.15713B ) ( 1 - 0.65111B**52 ) e_t
This is indeed a SARIMA model, i.e. Seasonal ARIMA (Auto-Regressive Integrated Moving Average) model with :
- seasonal differencing (once on 52 periods = simple seasonal differencing). The degree d of the seasonal differencing is 1 and s=52 is the length of the seasonal cycle.
- 1 is the order of the autoregressive part
- 1 is the order of the seasonal autoregressive part
- 1 is the order of the moving-average process
- 1 is the order of the seasonal moving-average process
- e_t is the independent disturbance, also called the random error
- you have no transfer functions as it is not SARIMAX (with some extra X-input time series)
Kind regards,
Koen
- Mark as New
- Bookmark
- Subscribe
- Mute
- RSS Feed
- Permalink
- Report Inappropriate Content
-
Thank you very much for your help!
April 27 – 30 | Gaylord Texan | Grapevine, Texas
Registration is open
Walk in ready to learn. Walk out ready to deliver. This is the data and AI conference you can't afford to miss.
Register now and lock in 2025 pricing—just $495!
- Ask the Expert: Wie kann ich Visual Studio Code als SAS Entwicklungsumgebung nutzen? | 11-Dec-2025
- DCSUG Online Winter Webinar | 11-Dec-2025
- Ask the Expert: Marketing Decisions Excellence: Turning Insights Into Business Impact | 16-Dec-2025
- SAS Bowl LVII, SAS Data Maker and Synthetic Data | 17-Dec-2025
- SAS Innovate 2026 | Grapevine, Texas | 27-Apr-2026