Stationarity Test with ADF Test vs Correlation Analysis

[Toni2]

Hi I have a time series, which i check it for stationarity using ADF test and arima proc 

proc arima data=&td19;
identify var=interest_rate stationarity=(adf=4);
run;
quit;

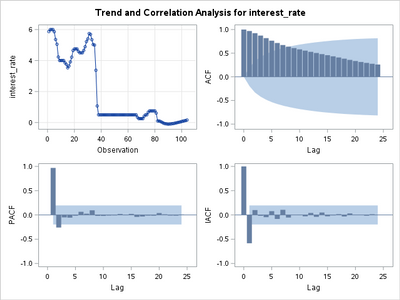
Below is the ADF test and trend & correlation analysis 

i started from the table from the bottom (trend model) and using the Tau compared it with 5% until to reject the null. i concluded that the series is stationary since 0.0315<0.05 zero mean model

However, when i see the ACF/PACF, based on my understanding, the series in not stationary. This is because the ACF decays slowly

My questions are : is this series stationary or not?

Augmented Dickey-Fuller Unit Root Tests
Type	Lags	Rho	Pr < Rho	Tau	Pr < Tau	F	Pr > F
Zero Mean	0	-2.7655	0.2517	-2.46	0.014
	1	-5.0099	0.1214	-2.26	0.0237
	2	-3.982	0.168	-2.21	0.027
	3	-5.0286	0.1207	-2.27	0.0228
	4	-4.2696	0.1532	-2.14	0.0315
Single Mean	0	-2.5618	0.7064	-1.71	0.4237	3.03	0.2995
	1	-6.4379	0.3047	-2.17	0.2186	2.78	0.3619
	2	-4.6272	0.4645	-1.92	0.3218	2.49	0.437
	3	-6.5225	0.2983	-2.17	0.2192	2.8	0.3657
	4	-5.2232	0.4056	-1.93	0.315	2.39	0.4685
Trend	0	-3.4578	0.9132	-1.23	0.8994	1.52	0.8742
	1	-16.6892	0.1154	-2.83	0.1917	4.32	0.3133
	2	-10.7554	0.3659	-2.18	0.4973	2.8	0.6186
	3	-19.6884	0.0597	-2.79	0.2033	4.29	0.3316
	4	-15.4981	0.1473	-2.39	0.3834	3.22	0.5402

[Ksharp]

the series in not stationary.

Maybe You need create a new variable = interest_rate - lag4(interest_rate) .
and use this new variable to run ADF ,and check if it is stationary .

[Toni2]

hi, thanks for your response. I have created the new variable :

newvar = interest_rate - lag4(interest_rate);

and run again the arima proc, below you can see the results 

The table shows that the Tau = 0.0045 < 0.05 which means that it is stationary. The ACF decays faster but PACT has 1st lag significant 

What is the conclusion? Does the below mean that the variable interest_rate is not stationary ? 

Augmented Dickey-Fuller Unit Root Tests
Type	Lags	Rho	Pr < Rho	Tau	Pr < Tau	F	Pr > F
Zero Mean	0	-10.5703	0.022	-2.35	0.0188
	1	-57.9428	<.0001	-5.44	<.0001
	2	-47.1978	<.0001	-4.35	<.0001
	3	-49.3153	<.0001	-4.28	<.0001
	4	-24.2331	0.0003	-3.01	0.003
Single Mean	0	-11.2029	0.092	-2.41	0.1419	2.9	0.3406
	1	-62.2964	0.0009	-5.57	<.0001	15.55	0.001
	2	-52.644	0.0009	-4.49	0.0005	10.07	0.001
	3	-55.7943	0.0009	-4.35	0.0007	9.55	0.001
	4	-27.2889	0.0011	-3.07	0.0327	4.74	0.049
Trend	0	-11.7463	0.3063	-2.48	0.3379	3.09	0.5647
	1	-64.2625	0.0003	-5.62	<.0001	15.8	0.001
	2	-55.4468	0.0003	-4.55	0.0022	10.33	0.001
	3	-57.8565	0.0003	-4.32	0.0045	9.46	0.001
	4	-28.5013	0.007	-3.07	0.1194	4.74	0.2431