- Home
- /
- Analytics
- /
- Forecasting
- /
- Re: PROC UCM forecast confidence interval: Why are the Level component...
- RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
- Mark as New
- Bookmark
- Subscribe
- Mute
- RSS Feed
- Permalink
- Report Inappropriate Content
I am developing a PROC UCM based forecast program that will cycle through many different transactions, determine the most appropriate model specification (choosing stochastic, deterministic, or remove for the slope, level, and seasonality components as well as keep/remove a predictor), and generate 18 months of weekly forecasts.
That being said, I'm struggling with extraordinarily wide CI's for some transactions I'm testing-- the CI itself is okay at the current date but the rate of its widening is the problem. It may be that a particularly troublesome one is indicative of a poor-fitting model. But I want to understand a little more of how that comes about. Constraints on time dictate that we use a uniform approach towards all of these series and limit our manual intervention. In the case of these wide intervals, the only way I know of to contain the CI is to set the variance=0 but that can result in much poorer-fitting models if output says it should stay in as stochastic.
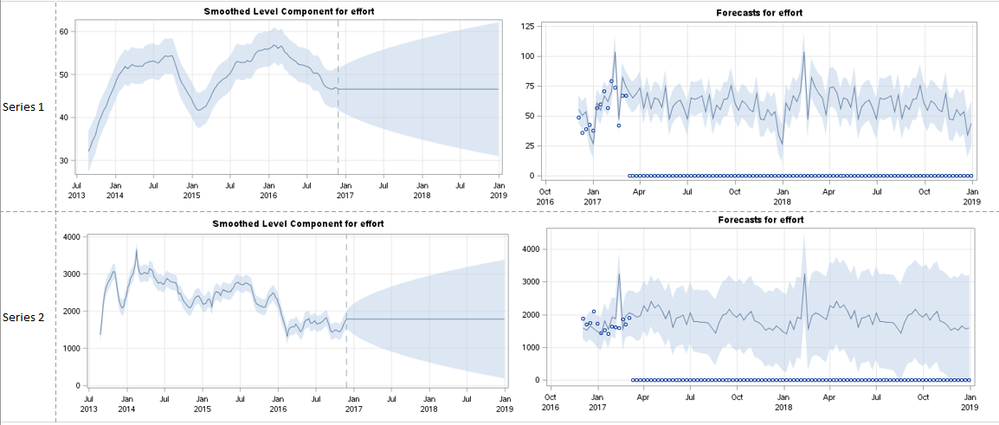
It may be helpful to provide two contrasting examples. Series 1 has a Mean of 64, St Dev of 17. Series 2 has a mean of 2400 and st dev of 664. The model speciications are identical: stochastic level, no slope, deterministic season (along with the other things that I'm not allowing to vary-- including the irregular statement, no cycle statement). I'm producing the smoothed level plots and they both show the conical CI. However the rate of change is much different, as the rate at which the standard error increases on the filtered level component is much different (which I'm assuming is the driver of the CI change). The error variance of the component is also much larger. Series 1 has a error variance of 4.4 (much less than the mean), whereas Series 2 has an error variance of 50,179 (25x larger than the mean).
Attached, I have shown the smoothed level and the forecast plots from Proc UCM. You can see how the CI gets much broader in series 2, despite the level CI not looking much different and in spite of the means and variances of the history.
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- RSS Feed
- Permalink
- Report Inappropriate Content
Your message discusses a few different points. I will try to address each one separately.
1. According to you, Series 2 has a mean of 2400 and st dev of 664. After a model is fit, the error variance is 50,179, i.e. standard dev is about 224. This appears OK. The model noise std dev is about a third of the observation std dev.
2. About the widening of the confidence band. Your models are essentially y = random walk + reg (including seasonal) + noise. You have provided the std dev of the noise (for both series) but not the variances of the random walk disturbances. For this model, the forecast variance increases linearly with the forecast horizon as, horizon * rw variance. So the confidence bands for the two series will differ according to their random walk disturbance variances.
Does this help?
- Mark as New
- Bookmark
- Subscribe
- Mute
- RSS Feed
- Permalink
- Report Inappropriate Content
Your message discusses a few different points. I will try to address each one separately.
1. According to you, Series 2 has a mean of 2400 and st dev of 664. After a model is fit, the error variance is 50,179, i.e. standard dev is about 224. This appears OK. The model noise std dev is about a third of the observation std dev.
2. About the widening of the confidence band. Your models are essentially y = random walk + reg (including seasonal) + noise. You have provided the std dev of the noise (for both series) but not the variances of the random walk disturbances. For this model, the forecast variance increases linearly with the forecast horizon as, horizon * rw variance. So the confidence bands for the two series will differ according to their random walk disturbance variances.
Does this help?
- Mark as New
- Bookmark
- Subscribe
- Mute
- RSS Feed
- Permalink
- Report Inappropriate Content
I was able to reduce the width by properly controlling for outliers. I had misinterpreted the function of the outlier detection in PROC UCM-- I had removed a variable that explained the largest of the outliers. Once I added it back in, the CI reduced significantly.
With other time series I still have wide CI's but the historical series is much less inherently forecastable. That being said, what you said is helpful if we decide to dig into those.
- Mark as New
- Bookmark
- Subscribe
- Mute
- RSS Feed
- Permalink
- Report Inappropriate Content
Rajesh
April 27 – 30 | Gaylord Texan | Grapevine, Texas
Registration is open
Walk in ready to learn. Walk out ready to deliver. This is the data and AI conference you can't afford to miss.
Register now and lock in 2025 pricing—just $495!
- Ask the Expert: Wie kann ich Visual Studio Code als SAS Entwicklungsumgebung nutzen? | 11-Dec-2025
- DCSUG Online Winter Webinar | 11-Dec-2025
- Ask the Expert: Marketing Decisions Excellence: Turning Insights Into Business Impact | 16-Dec-2025
- SAS Bowl LVII, SAS Data Maker and Synthetic Data | 17-Dec-2025
- SAS Innovate 2026 | Grapevine, Texas | 27-Apr-2026
