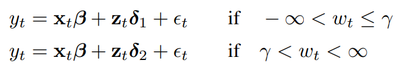- Home
- /
- Analytics
- /
- Forecasting
- /
- Hansen's threshold regression
- RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
- Mark as New
- Bookmark
- Subscribe
- Mute
- RSS Feed
- Permalink
- Report Inappropriate Content
Hi,
Does anyone have any idea about performing Hansen's threshold regression in SAS?
Or how can I find the document about it on the SAS platform?
Thanks,
Lynn
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- RSS Feed
- Permalink
- Report Inappropriate Content
Hello @LynnChen
At this time, there is no procedure that provides canned routine for Hansen(2000)'s threshold regression model directly. We may consider this functionality in the future, but at this time, you may consider following options:
For two regimes threshold regression like the following:
you may perform the estimation by looping over all possible gammas(or a grid of gammas) as discussed below:
- Get distinct w_t and sort them. assume they are {w_(i), i=1,…,T}, where w_(i) is the i-th smallest w. (that’s, all w_t are different, and T is the sample size).
- OLS regression y on (x, z), and record SSR as SSR_0.
- For i = 1 to T, OLS regress y on (x, u1, u2), where u1_t=z_t and u2_t=0 if w_t<=w_(i); otherwise, u1_t=0 and u2_t=z_t, and record SSR as SSR_i.
- Find the smallest SSR among SSR_i, i=0, …, T and the corresponding i; that’s, SSR_iStar<=SSR_i for any i.
- If i=0, no regime is needed; otherwise, gamma_hat=w_(iStar)
If T is big, take a grid of w_i; e.g., i might be in the range of 10%*T and 90%*T.
For multiple regimes, the combination of gammas should be looped over---but in that case, maybe the new procedure PROC BART is a better choice,
https://go.documentation.sas.com/doc/en/pgmsascdc/v_027/casstat/casstat_bart_details02.htm
Another alternative is similar to the following PROC MODEL switching regression example:
SAS Help Center: Switching Regression Example
which may provide an easier way to estimate this model, if you can accept that the solution is achieved by approximating the step function as the continuous function ProbNorm(.) --Note that this is a nonlinear optimization problem and the initial values or optimization method might matter.
Following is an example that estimates the threshold model using the PROC MODEL approach:
title1 'Threshold Regression Example';
data switch;
call streaminit('pcg', 12345);
do t = 1 to 1000;
e = rand('normal');
x = rand('normal');
z = rand('normal');
w = rand('uniform');
if(w<0.345) then y = 1 + 1.5*x + 2 * z + 0.5*e;
else y = 1 + 1.5*x - 2 * z + 0.5*e;
mylogL = (1/2)*( (log(2*3.1415)) +
log( 0.5**2 )
+ ((0.5*e)*( 1/0.5**2 )*(0.5*e)) ) ;
output;
end;
run;
proc means data=switch; var mylogL; run;
proc model data=switch;
parms sig1=1 int1 b1 b21 b22 gamma=0.5;
bounds 0.0001 < sig1;
a = (w - gamma)*100; /* Upper bound of integral */
d = probnorm(a); /* Normal CDF as an approx of switch */
/* Regime 1 */
y1 = int1 + x * b1 + z * b21 ;
/* Regime 2 */
y2 = int1 + x * b1 + z * b22 ;
/* Composite regression equation */
y = (1 - d)*y1 + d*y2;
/* Resulting log-likelihood function */
logL = (1/2)*( (log(2*3.1415)) +
log( sig1**2 )
+ (resid.y*( 1/sig1**2 )*resid.y) ) ;
errormodel y ~ general(logL);
fit y / method=marquardt converge=1.0e-6;
run;
quit;
I hope this helps!
- Mark as New
- Bookmark
- Subscribe
- Mute
- RSS Feed
- Permalink
- Report Inappropriate Content
Hello @LynnChen
At this time, there is no procedure that provides canned routine for Hansen(2000)'s threshold regression model directly. We may consider this functionality in the future, but at this time, you may consider following options:
For two regimes threshold regression like the following:
you may perform the estimation by looping over all possible gammas(or a grid of gammas) as discussed below:
- Get distinct w_t and sort them. assume they are {w_(i), i=1,…,T}, where w_(i) is the i-th smallest w. (that’s, all w_t are different, and T is the sample size).
- OLS regression y on (x, z), and record SSR as SSR_0.
- For i = 1 to T, OLS regress y on (x, u1, u2), where u1_t=z_t and u2_t=0 if w_t<=w_(i); otherwise, u1_t=0 and u2_t=z_t, and record SSR as SSR_i.
- Find the smallest SSR among SSR_i, i=0, …, T and the corresponding i; that’s, SSR_iStar<=SSR_i for any i.
- If i=0, no regime is needed; otherwise, gamma_hat=w_(iStar)
If T is big, take a grid of w_i; e.g., i might be in the range of 10%*T and 90%*T.
For multiple regimes, the combination of gammas should be looped over---but in that case, maybe the new procedure PROC BART is a better choice,
https://go.documentation.sas.com/doc/en/pgmsascdc/v_027/casstat/casstat_bart_details02.htm
Another alternative is similar to the following PROC MODEL switching regression example:
SAS Help Center: Switching Regression Example
which may provide an easier way to estimate this model, if you can accept that the solution is achieved by approximating the step function as the continuous function ProbNorm(.) --Note that this is a nonlinear optimization problem and the initial values or optimization method might matter.
Following is an example that estimates the threshold model using the PROC MODEL approach:
title1 'Threshold Regression Example';
data switch;
call streaminit('pcg', 12345);
do t = 1 to 1000;
e = rand('normal');
x = rand('normal');
z = rand('normal');
w = rand('uniform');
if(w<0.345) then y = 1 + 1.5*x + 2 * z + 0.5*e;
else y = 1 + 1.5*x - 2 * z + 0.5*e;
mylogL = (1/2)*( (log(2*3.1415)) +
log( 0.5**2 )
+ ((0.5*e)*( 1/0.5**2 )*(0.5*e)) ) ;
output;
end;
run;
proc means data=switch; var mylogL; run;
proc model data=switch;
parms sig1=1 int1 b1 b21 b22 gamma=0.5;
bounds 0.0001 < sig1;
a = (w - gamma)*100; /* Upper bound of integral */
d = probnorm(a); /* Normal CDF as an approx of switch */
/* Regime 1 */
y1 = int1 + x * b1 + z * b21 ;
/* Regime 2 */
y2 = int1 + x * b1 + z * b22 ;
/* Composite regression equation */
y = (1 - d)*y1 + d*y2;
/* Resulting log-likelihood function */
logL = (1/2)*( (log(2*3.1415)) +
log( sig1**2 )
+ (resid.y*( 1/sig1**2 )*resid.y) ) ;
errormodel y ~ general(logL);
fit y / method=marquardt converge=1.0e-6;
run;
quit;
I hope this helps!
April 27 – 30 | Gaylord Texan | Grapevine, Texas
Registration is open
Walk in ready to learn. Walk out ready to deliver. This is the data and AI conference you can't afford to miss.
Register now and lock in 2025 pricing—just $495!
- Ask the Expert: Wie kann ich Visual Studio Code als SAS Entwicklungsumgebung nutzen? | 11-Dec-2025
- DCSUG Online Winter Webinar | 11-Dec-2025
- Ask the Expert: Marketing Decisions Excellence: Turning Insights Into Business Impact | 16-Dec-2025
- SAS Bowl LVII, SAS Data Maker and Synthetic Data | 17-Dec-2025
- SAS Innovate 2026 | Grapevine, Texas | 27-Apr-2026