- Home
- /
- SAS Communities Library
- /
- The Principal Components of Principal Component Analysis
- RSS Feed
- Mark as New
- Mark as Read
- Bookmark
- Subscribe
- Printer Friendly Page
- Report Inappropriate Content
The Principal Components of Principal Component Analysis
- Article History
- RSS Feed
- Mark as New
- Mark as Read
- Bookmark
- Subscribe
- Printer Friendly Page
- Report Inappropriate Content
SAS programming concepts in this and other Free Data Friday articles remain useful, but SAS OnDemand for Academics has replaced SAS University Edition as a free e-learning option. Hit the orange button below to start your journey with SAS OnDemand for Academics:
I have been intrigued and fascinated by Principal Component Analysis for some time, but haven’t had the need to really learn it (or so I thought). I have recently been moved into another position at work, and lo and behold my boss and I were talking and she said that the data we’re looking at might benefit from PCA. So, I decided it was time I buckle down and get a handle on this topic.
First, a brief definition, coming from the SAS Documentation on PCA:
[PCA]…is appropriate when you have obtained measures on a number of observed variables and wish to develop a smaller number of artificial variables (called principal components) that will account for most of the variance in the observed variables…
OK, so far so good! The next section talks about how PCA is effective at reducing redundancy in the variables, where redundant means some of the variables are correlated with one another, possibly because they are measuring the same thing. The 
On closer inspection, you realise that Questions 1 – 4 all deal with satisfaction with the supervisor, and 5 – 7 deal with the employee’s feelings about their pay. If we run a correlation, we may see a very clear split between the two groups of questions, indicating variable redundancy.
So, let’s look at an example using some open data I found.
Get the Data
The data is looking at victims of crimes from the FBI Database, and can be found here.
Get Started with SAS OnDemand for Academics
Get the data ready
I had to do some cleanup to the data (removing footnotes, unmerging cells, deleting the rows / column with totals, and moving the “Crimes Against Property” and “Crimes Against Person” to a new column). As usual, I used the Data Import task to bring the data into SAS University Edition.
The results
The code itself is fairly straightforward:
proc princomp data=work.import plots= score(ellipse ncomp=3);
id type;
run;
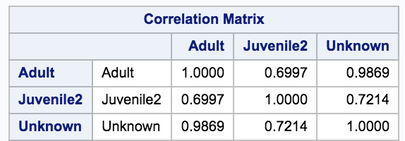
When I run it, I get a bunch of tables and graphs and I’m going to go through what I think appear to be the key ones. The first is the Correlation Matrix:
This is showing us the correlations between the original variables. Before conducting a PCA< you want to check the correlations between the variables. If any of the correlations are too high (greater than 0.9) you may need to remove one of the variables from the analysis, as the two variables seem to be measuring the same thing. If the correlations are too low, say below 0.1, then one or more of the variables might be its own Principal Component, which does not help us reduce the number of variables. In our example, we should probably remove the “Unknown” age category as it’s extremely high correlation to Adult will cause us problems.
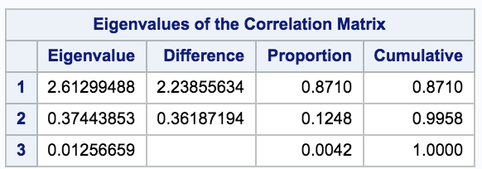
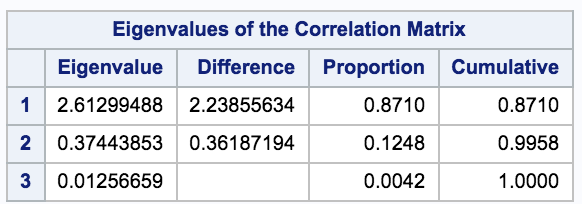
The next table has what are called Eigenvalues for the Correlation Matrix; the first time I heard this, I was stumped – never having come across the term before, I had no idea what it was. Basically, it’s a way to show variance – the first component in the list will always have the highest variance, followed by the second highest, etc.
I have to admit I get the concept of what an eigenvalue is, but I am not comfortable enough with these concepts to offer a solid explanation. I am hoping someone can provide some assistance in the comments, because I would really like to better understand this concept. I am also struggling to figure out what Component 1 is – based on the proportion column, it explains 87% of the variance, but I can’t figure out how to know if it’s Adult / Unknown, Adult / Child, etc.
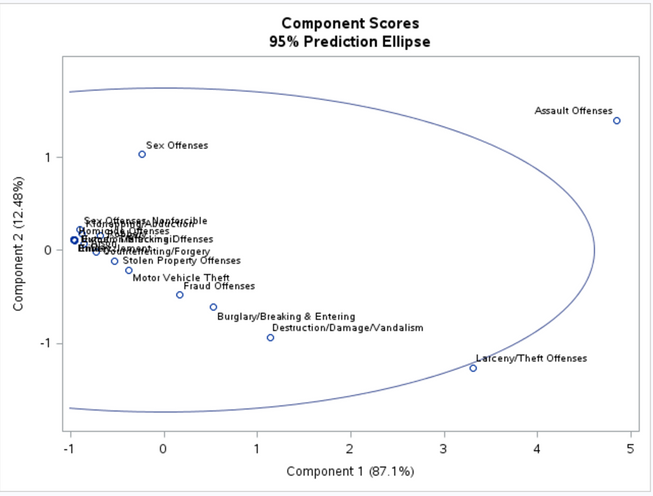
I’m going to turn my attention to one of the graphs that the PROC PRINCOMP created. It is a scatter plot with a 95% Ellipse, comparing Components 1 and 2 (the percentages are the proportion of the variation we saw in the second image above).
Very clearly, Larceny/Theft and Assault are “extreme” outliers, and Sex Offenses is an outlier (within the 95% but clearly outside the cluster). When I sort the data by Adult victims and then by Juvenile victims, it’s very apparent these three have the highest volume.
I'm sure I'm barely scratching the surface of PCA, and I look forward to seeing what comments and addtional information people can post!
Now it’s your turn!
Did you find something else interesting in this data? Share in the comments. I’m glad to answer any questions.
- Mark as Read
- Mark as New
- Bookmark
- Permalink
- Report Inappropriate Content
DarthPathos wrote:
The next table has what are called Eigenvalues for the Correlation Matrix; the first time I heard this, I was stumped – never having come across the term before, I had no idea what it was. Basically, it’s a way to show variance – the first component in the list will always have the highest variance, followed by the second highest, etc.
I have to admit I get the concept of what an eigenvalue is, but I am not comfortable enough with these concepts to offer a solid explanation. I am hoping someone can provide some assistance in the comments, because I would really like to better understand this concept. I am also struggling to figure out what Component 1 is – based on the proportion column, it explains 87% of the variance, but I can’t figure out how to know if it’s Adult / Unknown, Adult / Child, etc.
Your original three variables have a certain amount of variability. When you look at component 1, it captures 87% of the total variability of the original three variables. (Or another way of saying this is that if you tried to model all three of your original variables with just component 1, 87% of the variability is explained and the other 13% is the residual, unexplained by component 1). This is the same idea that any other modeling technique uses ... explaining variability.
Component 2 explains another 12.48% of the variability of the original three variables, and Component 1 and 2 together explain 99.58% of the variability of the orginal three variables.
The components themselves are linear combinations of all three variables. The eigenvectors (also called loadings) tell you what the linear combinations are. So when you say "but I can’t figure out how to know if it’s Adult / Unknown, Adult / Child, etc.", it's all three original variables, added together with loadings/eigenvectors describing the relative weight of each of the original variables. If the loadings for component 1 are 0.3 for Adult, 0.08 for Juvenile2 and -0.22 for Unknown (I made those loadings up as the actual loadings/eigenvectors are not provided), then component 1 is really 0.3*Adult + 0.08*Juvenile - 0.22*Unknown (where the values for Adult, Juvenile and Unknown are properly scaled to match the scaling used to compute the PCA analysis). This linear combination determines the position of each data point on the two-dimensional plot of component scores shown.
- Mark as Read
- Mark as New
- Bookmark
- Permalink
- Report Inappropriate Content
Hi @PaigeMiller
Thanks for your reply! Quoting your response, you said
So when you say "but I can’t figure out how to know if it’s Adult / Unknown, Adult / Child, etc.", it's all three original variables, added together with loadings/eigenvectors describing the relative weight of each of the original variables. If the loadings for component 1 are 0.3 for Adult, 0.08 for Juvenile2 and -0.22 for Unknown (I made those loadings up as the actual loadings/eigenvectors are not provided),
Your uncertainty is what i am confused about - I don't know how to align the "Component" with the variable. I've done a bit of reading, including the SAS Documentation and the article by Leslie Smith which is a great introduction to the math behind PCA, but I get lost in the formulae and math (I love math but am not a mathematician or statistician, or ever even took anything in University beyond Introduction to Stats).
Really appreciate your time and any thoughts or suggestions for additional reading.
Have a great day!
Chris
- Mark as Read
- Mark as New
- Bookmark
- Permalink
- Report Inappropriate Content
Sometimes, the language of PCA itself can be a barrier to learning, and that might be the problem here.
I don't know how to align the "Component" with the variable
I don't know what you mean by "align", but the relationship is what I described before, where the component is a linear combination of all three original variables, with the loadings/eigenvectors being the weights in the linear combinations.
- Mark as Read
- Mark as New
- Bookmark
- Permalink
- Report Inappropriate Content
Hey Paige - Gotcha - this makes more sense now and I'll go back and re-read everything with this newfound understanding 🙂 Thanks for clarifying and I hope you have a great evening
Chris
- Mark as Read
- Mark as New
- Bookmark
- Permalink
- Report Inappropriate Content
Hi @DarthPathos
The first eigenvalue accounts for about 87.10% of the total variance, the second eigen value accounts for about 12.48%. Eigenvalues sum to the total variance. Hence, the first two eigenvalue accounts for about 99.58% of the total variance. We can go by criteria where number of eigenvalues >1 (according to Kaiser – Guttman Criterion). Hence, we retain first two principal components.
What is your eigen vector?

The 2025 SAS Hackathon has begun!
It's finally time to hack! Remember to visit the SAS Hacker's Hub regularly for news and updates.
SAS AI and Machine Learning Courses
The rapid growth of AI technologies is driving an AI skills gap and demand for AI talent. Ready to grow your AI literacy? SAS offers free ways to get started for beginners, business leaders, and analytics professionals of all skill levels. Your future self will thank you.
- Find more articles tagged with:
- Data for learning
- Free Data Friday