- Home
- /
- SAS Communities Library
- /
- How to Train Generalized Additive Models (GAMs) in Model Studio
- RSS Feed
- Mark as New
- Mark as Read
- Bookmark
- Subscribe
- Printer Friendly Page
- Report Inappropriate Content
How to Train Generalized Additive Models (GAMs) in Model Studio
- Article History
- RSS Feed
- Mark as New
- Mark as Read
- Bookmark
- Subscribe
- Printer Friendly Page
- Report Inappropriate Content
In a companion blog, "Accuracy vs. Interpretability? With Generalized Additive Models (GAMs), You Can Have Both," we provide an overview of generalized additive models (GAMs) and their beneficial features. GAMs are appealing because they strike a nice balance between flexibility and performance while maintaining a high degree of interpretability.
This article provides the complete step-by-step instructions to reproduce the data analysis in the companion blog, to show you how easy it is to use Model Studio to train a GAM and compare it to other machine learning models. To do that, let’s revisit an example from Lamm & Cai (2020) that trains a GAM to predict the probability that a mortgage applicant will default on a loan. See Example 2 in Lamm & Cai (2020) for more information about the example and the Hmeq data set.
For a snapshot of this example, watch the following demo video:
Data & Project Setup
First, let’s run the following code within SAS® Studio in SAS® Viya® to start a new session with a SAS® Cloud Analytic Services (CAS) server, assign the Mycas libref to the Casuser caslib, and create the data set used by Lamm & Cai (2020) as the in-memory table HmeqLC in the Casuser library. Here, the DATA step code differs from Lamm & Cai (2020) in that it renames the processed data set to distinguish it from the original Hmeq data set. It also includes the PROMOTE= data set option to create the CAS table with global scope so that it is accessible from Model Studio.
cas;
libname mycas cas caslib="casuser";
data mycas.hmeqLC(promote=yes);
set sampsio.hmeq;
if cmiss(of _all_) then delete;
if CLAge > 1000 then delete;
part = ranbin(1,1,0.2);
run;
Next, let’s switch to Model Studio, part of SAS® Visual Data Mining and Machine Learning, and use the GAM node[1] to train the GAM. To do this, access the Applications menu in the upper-left corner and select Build Models (Figure 1).
Figure 1 Open Model Studio via the Build Models selection in the Applications menu.
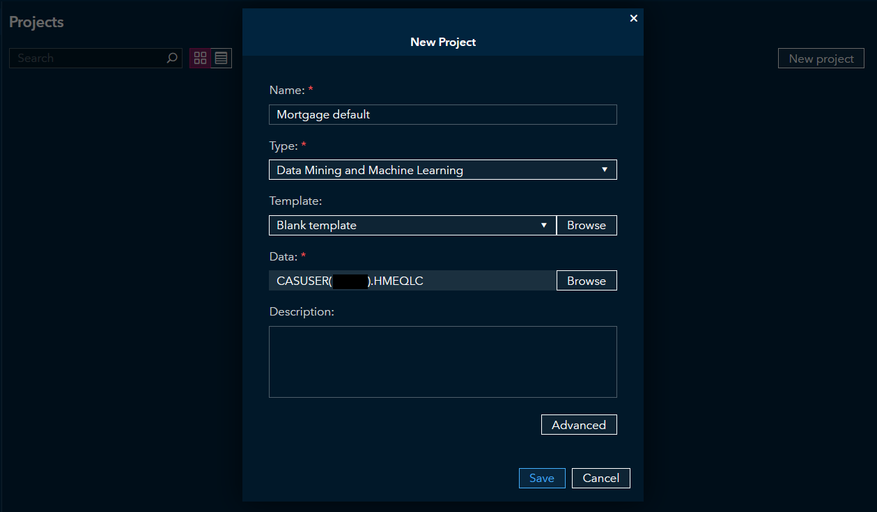
Within Model Studio, select New project and create a Data Mining and Machine Learning project with the HmeqLC data table (Figure 2).
Figure 2 Create a new Model Studio project with the preprocessed data set, HmeqLC.
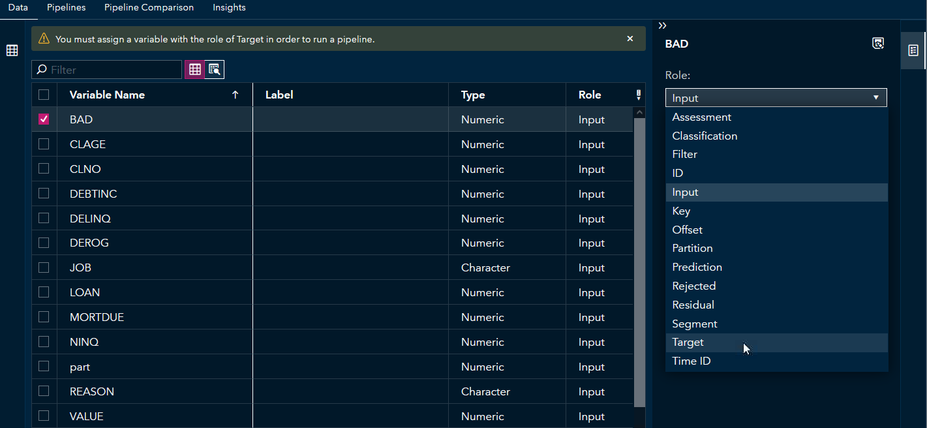
In the Data tab, select the variable BAD and assign it to the role of Target (Figure 3).
Figure 3 Set the variable BAD as the target.
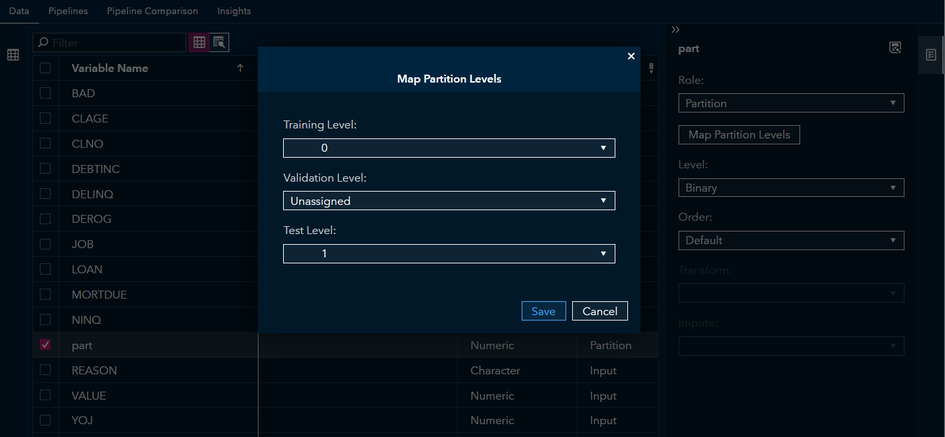
Next, select the part variable, assign it to the role of Partition, select Map Partition Levels, and map Training Level to 0 and Test Level to 1 (Figure 4).
Figure 4 Map the levels to the partition variable to match Lamm & Cai (2020).
Train a GAM with the GAM Node
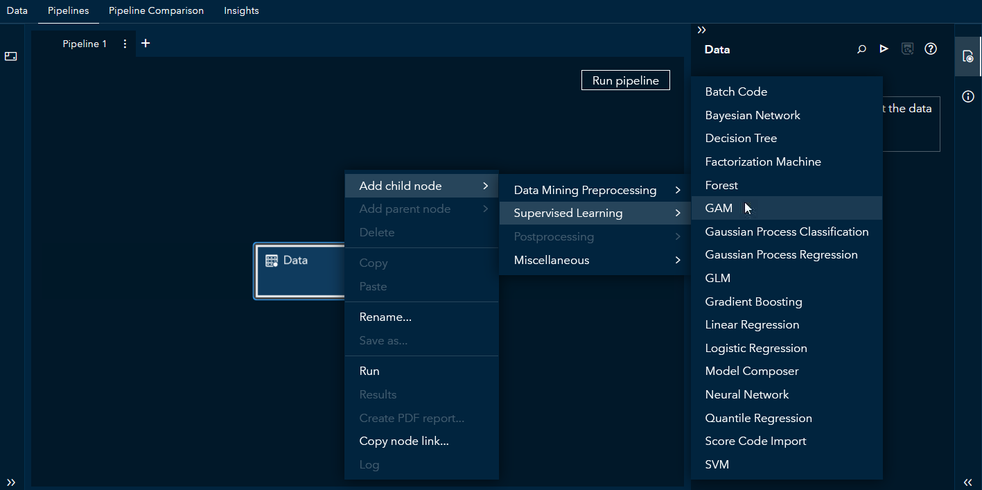
Now you are ready to switch to the Pipelines tab to create a model building pipeline. To add a GAM node to your pipeline, right-click the Data node → Add child node → Supervised Learning → GAM (Figure 5).
Figure 5 Steps to add the GAM node to your pipeline.
The GAM node enables you to train a GAM without the need to write any code. The node contains a variety of options to customize your analysis, such as the interval target probability distribution[2], the target link function, effects options, and options related to the chosen selection method (Figure 6).
Figure 6 The GAM node includes many options to customize your model.
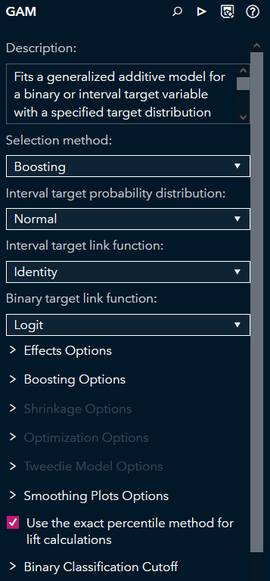
For example, you can use the following steps to train a model similar to the one in Lamm & Cai (2020):
- Expand the Effects Options group
- Click the button next to the Bivariate Splines group to include bivariate splines in the model[3]
- Select Use all observations to construct spline basis functions
- Expand the Boosting Options group
- Set Learning rate to 0.2
- Set Early stopping stagnation to 10 and Early stopping tolerance to 0.0005
- At the top of the GAM node, click
to run the node
Results
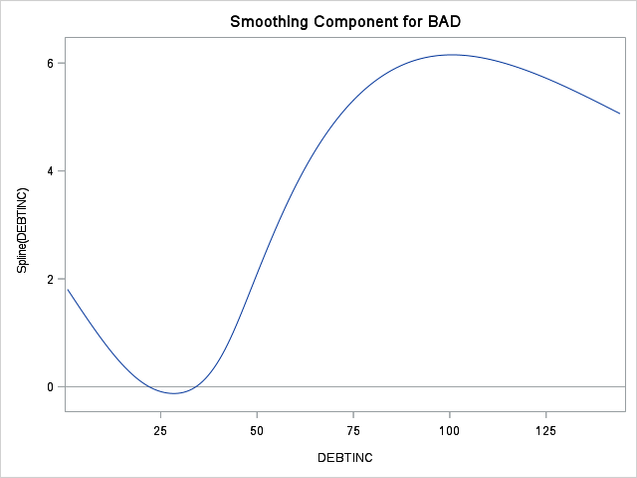
After you use the node to train the model, right-click the GAM node and select Results to view the model’s results. For the effects in the final model, the results include smoothing component plots for the spline terms and parameter estimates for the parametric terms. For example, the results include a smoothing component plot for the Spline(Debtinc) term (Figure 7). You can see that the probability of default is generally higher for an applicant who has a high debt-to-income ratio and the relationship is nonlinear.
Figure 7 The probability of default is generally higher for higher debt-to-income ratios.
Given the importance of the smoothing component plots, the GAM node includes options that govern the display of the plots. For example, you can select Use a common vertical axis to use the same y-axis range for each univariate spline plot. This facilitates comparisons of the magnitudes of the estimated spline effects on the predicted target.
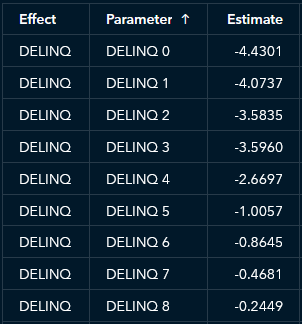
In addition, the ability to interpret the parametric effects like you would with a logistic regression model is another way in which the GAM’s results are relatively easy to understand. For example, an applicant with more delinquent credit lines has a higher predicted probability of default, on average (Figure 8).
Figure 8 More delinquent credit lines typically correspond to a higher probability of default.
Model Comparison
Now that you have used the GAM node to train a GAM, let’s train a few other models for comparison, which you can easily do in Model Studio. Repeat the previous steps to add a Supervised Learning node to your pipeline to add the Gradient Boosting, Logistic Regression, Neural Network, and SVM nodes, and then click Run pipeline to train and compare all these models. Right-click the Model Comparison node to view the Results. If you sort the algorithms by Misclassification Rate, you see that the GAM ranks second (Figure 9).
Figure 9 The GAM outperforms some of the more complex models but maintains interpretability.
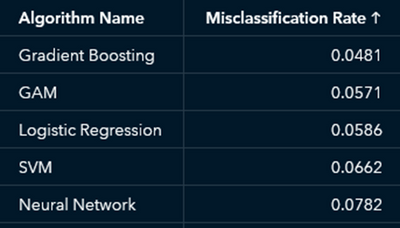
Even though the GAM has a slightly higher misclassification rate, it is more interpretable than the champion gradient boosting model and still outperforms other complex models such as SVM and neural network.
As you can see, Model Studio enables you to easily train a GAM alongside other common machine learning models and to compare model performance. This is done in just a few clicks and keystrokes to make analytics more accessible to a broader range of people, empowering them to use data to improve decision making.
Acknowledgments
The author is grateful to Wendy Czika, Michael Lamm, Weijie Cai, and Brett Wujek for their help and feedback during the development of the GAM node. Thanks also to Wendy Czika, Anna Brown, and Ed Huddleston for their helpful comments on an early draft.
Additional Resources
In addition to the resources linked in the article, the following resources provide further information about training GAMs with SAS:
- Introducing the GAMSELECT Procedure for Generalized Additive Model Selection (SAS Global Forum 2020 presentation)
- The GAMSELECT Procedure documentation
- The GAMMOD Procedure documentation
[1] Available in SAS Viya Stable 2020.1.1 (December 2020) and Long-Term Support 2021.1 (May 2021).
[2] A binary target variable, such as BAD, always uses the binary distribution.
[3] This option adds bivariate splines for all pairwise combinations of the interval inputs, whereas the GAM in Lamm & Cai (2020) includes only a few bivariate spline terms.
- Mark as Read
- Mark as New
- Bookmark
- Permalink
- Report Inappropriate Content
I read your blog and I quoted
For example, if you are interested in predicting whether an incoming email is spam,
or you want to predict the number of people dining in a restaurant,
the linear regression model is inappropriate.
This is because the target variables for those applications violate the model’s normality assumption.
But @Rick_SAS might do not agree with your argument .
- Mark as Read
- Mark as New
- Bookmark
- Permalink
- Report Inappropriate Content
Hi KSharp,
I assume you are thinking about my article, "On the assumptions (and misconceptions) of linear regression," in which I discuss the fact that normality of variables is not an assumption of ordinary least-squares regression. However,
the same article mentions other assumptions of OLS that are always necessary. The first and most important assumption is that the model can correctly specify the form of the underlying data-generating process. Brian's point is that OLS can't model binary responses, nonnegative count data, etc., because a linear predictor might make invalid predictions (such as negative counts). That is why he says that "the linear regression model is inappropriate." Generalized linear models, GAMS, and the other models that Brian discusses are the correct ways to model those response variables.
- Mark as Read
- Mark as New
- Bookmark
- Permalink
- Report Inappropriate Content
Rick,
So you mean "linear regression model" stands for OLS (a.k.a PROC REG) ?
Brian's point is that OLS can't model binary responses, nonnegative count data, etc.,
because a linear predictor might make invalid predictions (such as negative counts).
But any symmetry distribution would lead to this issue, not just Normal distribution ,right ?
- Mark as Read
- Mark as New
- Bookmark
- Permalink
- Report Inappropriate Content
I don't want to have this debate with you in this thread. It would distract from Brian's nice and useful article on using GAMs to model data. Let's thank him for his contribution and not quibble about one word among 2,500.
SAS AI and Machine Learning Courses
The rapid growth of AI technologies is driving an AI skills gap and demand for AI talent. Ready to grow your AI literacy? SAS offers free ways to get started for beginners, business leaders, and analytics professionals of all skill levels. Your future self will thank you.