regression diagnosis

[aha123]

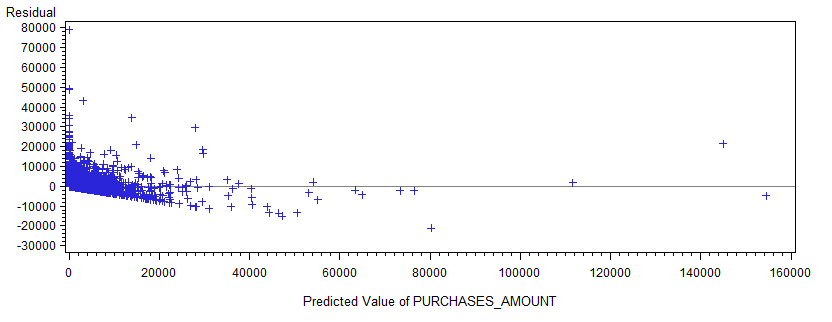
Most textbooks give easy examples for how to diagnosis a regression model. But in real world, I often encountered residual plots like the attached one.

It was produced by the following SAS code. I want to know what remedy actions I should take for a residual plot like this one.

/* purchases_amount: total purchase amount by a consumer in last 6 months

   apparel: purchase amount in apparel in last 6 months

   entertainment: purchase amount in enterment in last 6 months

    travel: purchase amount in last 6 months

*/

proc reg data=cc_seg;

  model purchases_amount = apparel enternment travel;

  output out=cc_res r = r p = p;

run; quit;

proc gplot data=cc_res;

  plot r*p / vref=0;

run; quit;

[Rick_SAS]

For variables that encompass several order of magnitudes, a good rule of thumb is to apply a log transformation. For these data, I'd try y=log10(purchases_amount) and use Y as the response variable.

Also, PROC REG will compute regression diagnostic plots for you. Just turn on ODS graphics:

ods graphics on;

The "residual vs. predicted" [;pt is the upper left in a panel of diagnostic plots. See Figure 76.12 in the PROC REG doc: http://support.sas.com/documentation/cdl/en/statug/63962/HTML/default/viewer.htm#statug_reg_sect004....

[plf515]

Rick gave one good idea, above. That will deal with the skewness of the predicted values (which is presumably reflecting the skewness of the dependent variable).

I notice that you seem to have a few very badly predicted points near the low end; given your comments about what the data means, this looks like people who bought a car or some other very expensive item (could be down payment on a house, perhaps). Then there are people whose predicted value is very high.

It might be that you really want to model two different things; in this case a loess regression might work well. This doesn't mean that the log idea, suggested by Rick is wrong, it isn't wrong. But it may not be the ideal solution to your problem.