PROC PLS root mean PRESS calculation

[jroberts1992]

Dear SAS community,

I am running PLS on spectra data and I am trying to clarify how root mean press is calculated in full leave-one-out cross validation. I have the following model:

PROC PLS DATA=df cv=one;

MODEL depvar=nm400-nm1900;

OUTPUT out=outputdata PRESS=press;

run;

As I understand it, the OUTPUT PRESS option gives the residual value between the observed and predicted for each observation when that observation is "held out" from the data set. First, is this correct?

Now if I calculate the root mean press for the data set from the output dataset PRESS values, the value is different than the root mean press for the number of factors which minimizes PRESS. From the analyses I've seen, the root mean PRESS output by SAS seem to vary between 0 and 1 (or at least near 1), so my guess is there is some sort of normalization occuring in these calculations. I can't find any source detail if or how SAS is normalizing the root mean PRESS values. I've also tried a multitude of transformations to try and replicate the root mean PRESS output by the model to no avail.

Can anyone shed any light on this?

Thank you,

Jordan

[PaigeMiller]

Last time I checked, the SAS documentation on how PRESS is computed was pretty weak. Now maybe it has improved, but one thing I will state as a definite fact, is that I am too lazy to check. I will point out that as I was going to check, I came across this horrible mis-documentation at http://support.sas.com/documentation/onlinedoc/stat/indexproc.html#stat143 and I threw my hands up and stopped right there.

Hey @ChrisHemedinger, to whom should we complain so this can be fixed?

As I understand it, the OUTPUT PRESS option gives the residual value between the observed and predicted for each observation when that observation is "held out" from the data set. First, is this correct?

As I understand what you're saying, I believe it to be correct. I would make a minor wording change to say "...when that observation is 'held out' from the PLS model".

From the analyses I've seen, the root mean PRESS output by SAS seem to vary between 0 and 1 (or at least near 1), so my guess is there is some sort of normalization occuring in these calculations.

I am not aware of this statistic being normalized somehow; even the name "Predicted Residual Sum-of-Squares" indicates it is a sum (of squares) and not some normalized quantity.

[ChrisHemedinger]

@PaigeMiller - I've passed your comment on to the person in R&D who maintains this page.

[PaigeMiller]

@ChrisHemedinger As they say here in Buffalo, NY, muchas gracias.

[ChrisHemedinger]

Speaking as a Buffalo native, fuggedaboutit.

[ChrisHemedinger]

@PaigeMiller - doc page is now fixed!

[Rick_SAS]

The PRESS statistic is documented among the residual and influence statistics. PROC REG has a little bit, but the main reference is the "Predicted and Residual Values" section of the "Introduction to Regression Procedures" chapter. The doc says

"The predicted residual for observation i is defined as the residual for the ith observation that results from dropping the ith observation [and refitting the model]. The sum of squares of predicted residual errors is called the PRESS statistic:"

In practice, there is no need to refit the model since you can efficiently compute the predicted residual by the formula

PResid[i] = Resid[i] / (1-h[i])

where h[i] is the ith leverage value, sometimes called the "hat diagonal".

Could this be the missing "normalization factor" you are looking for?

Here is a program that uses PROC REG to output the PRESS statistic, then uses a DATA step to accumulate the sum of the squares of the quantities Residual / (1 - h[i]). The DATA step validates the PRESS statistic in the OUTEST= data set.

proc reg data=sashelp.class outest=est plots=none;
model weight = height age / press influence;
ods output  OutputStatistics=out;
quit;

proc print data=est; var _PRESS_; run;

data PRESS;
set out end=eof;
PRESS + (Residual / (1 - hatDiagonal))**2;
if eof then output;
keep PRESS;
run;

proc print data=PRESS; run;

[PaigeMiller]

The PRESS statistic is documented among the residual and influence statistics. PROC REG has a little bit, but the main reference is the "Predicted and Residual Values" section of the "Introduction to Regression Procedures" chapter. 

Aha! This is why I remember not being satisfied with the PROC PLS documentation ... the information isn't in PROC PLS documentation, it is elsewhere in the SAS documentation. There ought to be a hyperlink in the PROC PLS documentation to this "Predicted and Residual Values" section. A documentation deficiency!! Can we get this fixed, @Rick_SAS and @ChrisHemedinger?

In practice, there is no need to refit the model since you can efficiently compute the predicted residual by the formula

PResid[i] = Resid[i] / (1-h[i])

where h[i] is the ith leverage value, sometimes called the "hat diagonal".

While this is certainly true for Ordinary Least Squares Regression, I am not convinced it is true for a bilinear method such as Partial Least Squares Regression. I haven't worked through the math. But even if it is true, dividing by the value (1-h[i]) is not a normalization of any sort that forces the resulting value to be between 0 and 1, as the original questioner asked.

[PaigeMiller]

Upon reading the original message more carefully, the question was about root mean PRESS being between 0 and 1 and not PRESS being between 0 and 1. Nevertheless, the answer is the same, the root mean press does not have to be between 0 and 1, as the example at http://documentation.sas.com/?cdcId=pgmmvacdc&cdcVersion=9.4&docsetId=statug&docsetTarget=statug_pls... shows (where I ahve added CV=ONE into the PROC PLS statement). So there is no normalization going on.

I believe that the zero to one interpretation of the Root Mean PRESS is to give you a cutoff showing that the PLS Model is fitting better than simply fitting the mean. A root mean PRESS of 1 indicates the model is just as good a predictor as fitting the mean, a number > 1 indicates the model is predicting worse than fitting the mean, and a number < 1 indicates that the model is predicting better than fitting the mean (which is what you want). A zero root mean PRESS indicates the model fits exactly.

[jroberts1992]

Thanks for your replies.

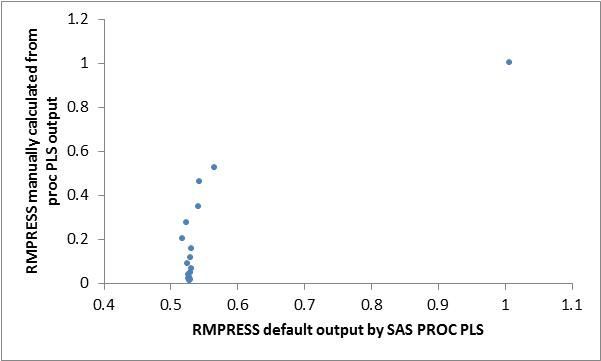
Rick_SAS, I applied your code with the output from my proc PLS model. The root mean PRESS from the (resid[i]/1-h)**2 formula gave the same output for each observation as using the PRESS ouput option from the PROC PLS model and squaring that value. When I take the root mean PRESS (sqrt(sum(press)/count(press)) from these manually calculated values and plot them against the RMPRESS table output by PROC PLS by default, it would appear values are close to some logarithmic transformation.

[PaigeMiller]

Perhaps ... because the formula given by Rick works for OLS (PROC REG), but not for PLS (PROC PLS). If I had the time, I would dig into this more.

[TET_34]

additional

https://support.sas.com/documentation/onlinedoc/stat/141/glmselect.pdf p.3892