- Home
- /
- Analytics
- /
- Stat Procs
- /
- Re: PROC PHREG for time-varying exposure with non-proportional hazard
- RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
- Mark as New
- Bookmark
- Subscribe
- Mute
- RSS Feed
- Permalink
- Report Inappropriate Content
Dear all,
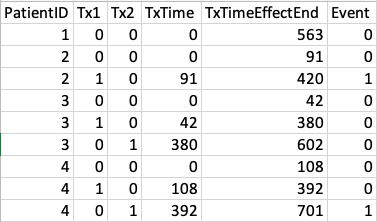
I am trying to conduct an analysis that involves both time-dependent exposure and time-dependent coefficient (non-proportional hazard). Patients were enrolled in the study when they were diagnosed with a specific disease, and some of them received pharmacologic therapies during their clinical courses at various timings. Both Tx1 and Tx2 are one-time infusions, and they are expected to have waning effects over time (Tx2 can be administered only after Tx1). Research questions are the effects of Tx1 and Tx2 to prevent the event outcome, as well as how fast the protective effects wane over time. A sample of our dataset structure is shown below:
Patient ID is a unique identifier for patients, and Tx1/Tx2 are indicator dummy variables for the treatment status (patients with no therapy as 0). For example, the first patient (PatientID = 1) received no therapy and censored on day 563, and the last patient (PatientID = 4) received Tx1 on day 108 and Tx2 on day 392, then experienced an event outcome on day 701.
When ignoring non-proportional hazard, my syntax was something like this:
==
proc phreg data = work.dataset;
model (TxTime, TxTimeEffectEnd)*Event(0) = Tx1 Tx2;
id PatientID;
run;
==
In my previous projects without time-dependent exposure, I used programming statements in proc phreg to include interaction term with time (log-transformed) when I needed to consider non-proprotional hazard. Syntax was like this (one row per patient):
==
proc phreg data = work.dataset;
model Time*Event(0) = Tx Tx_Time;
Tx_Time = Tx*log(Time + 1);
run;
==
Obviously, I can't just use this syntax because the current dataset involves a pair of failure-time variables ("(t1,t2)" style syntax) rather than one ("Time" in this example).
At first, I thought about this syntax but I am not sure if t2 ("TxTimeEffectEnd" in this example) is instantaneous value at each time point and correctly consider time-effect interaction to estimate non-proportional hazard.
==
proc phreg data = work.dataset;
model (TxTime, TxTimeEffectEnd)*Event(0) = Tx1 Tx2 Tx1_Time Tx2_Time;
Tx1_Time = Tx1*log(TxTimeEffectEnd - TxTime +1);
Tx2_Time = Tx2*log(TxTimeEffectEnd - TxTime +1);
id PatientID;
run;
==
Does this syntax correctly model time-varying coefficient in a model with a pair of failure-time variables?
I also tried step-function to model non-proportional hazards but it did not work well because of the highly variable exposure timings of therapies and sparse outcome events.
Thank you so much for your inputs!
- Mark as New
- Bookmark
- Subscribe
- Mute
- RSS Feed
- Permalink
- Report Inappropriate Content
It's very late over here, so I haven't read your post in-depth.
Just want to say that
for handling the non-proportional hazards situation in time-to-event analysis
, you can use these methods :
- The RMSTREG procedure : fits generalized linear models to the RMST. (RMST = Restricted Mean Survival Time)
- Piecewise exponential regression allows for an early and late effect of treatment comparison. it is especially useful when the non-proportional hazards pattern is cross-over. Piecewise exponential regression can be fitted with SAS Proc MCMC.
BR,
Koen
- Mark as New
- Bookmark
- Subscribe
- Mute
- RSS Feed
- Permalink
- Report Inappropriate Content
Thanks, Koen! I'll check PROOC RMSTREG out to see if it fits the purpose of my project.
Michi
SAS Innovate 2025: Save the Date
SAS Innovate 2025 is scheduled for May 6-9 in Orlando, FL. Sign up to be first to learn about the agenda and registration!
ANOVA, or Analysis Of Variance, is used to compare the averages or means of two or more populations to better understand how they differ. Watch this tutorial for more.
Find more tutorials on the SAS Users YouTube channel.